Toleranciaintervallumok
Ez a szakasz az egyoldalú és kétoldalú toleranciaintervallumok statisztikai adatait tartalmazza.
Normális eloszláson alapuló intervallumok
Egyoldalú intervallum
Az egyoldalú intervallum kiszámítása a következőképpen történik:
alsó határ = 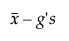
felső határ = 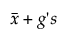
ahol
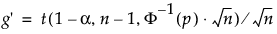
s a szórás
t a kvantilis a non-központi t-eloszlásból
Φ-1 a standard normál kvantilis
Kétoldalas intervallum
A kétoldalas intervallumot a következőképpen számítjuk ki:
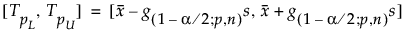
ahol s a szórás és g(1-α/2; p,n) egy konstans.
A g meghatározásához tekintsük a populációnak azt a hányadát, amelyet a tűrésintervallum megragad. Tamhane és Dunlop (2000) ezt a hányadot a következőképpen adja meg:
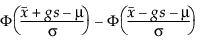
ahol Φ a standard normál cdf-et (kumulatív eloszlásfüggvény) jelöli.
Ezért g a következő egyenletet oldja meg:
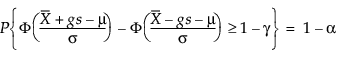
ahol 1 – γ az összes jövőbeli megfigyelésnek a tűrésintervallumba eső hányada.
A normális eloszláson alapuló tűrésintervallumokról további információt a J.1. táblázatban talál.a, J.1b, J.6a és J.6b táblázatokat Meeker et al. (2017).
Nonparametrikus intervallumok
Egyoldalú alsó határ
Az alsó 100(1 – α)%-os egyoldalú tűréshatár, amely egy n méretű mintából vett eloszlás legalább β arányát tartalmazza, az x(l) rendszám-statisztika. Az l indexet a következőképpen számítjuk ki:
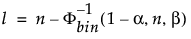
ahol Φ-1bin(1-α, n, β) a binomiális eloszlás (1 – α)-dik kvantora n próbával és β valószínűséggel.
A tényleges megbízhatósági szint kiszámítása a következőképpen történik: Φbin(n-l, n, β), ahol Φbin(x, n, β) annak a valószínűsége, hogy a binomiális eloszlású véletlen változó n próbával és β siker valószínűséggel kisebb vagy egyenlő x-szel.
Megjegyezzük, hogy az alsó egyoldalú eloszlásmentes tűrésintervallum kiszámításához az n mintaméretnek legalább akkorának kell lennie, mint 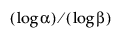 .
.
Egyoldalú felső határ
A felső 100(1 – α)%-os egyoldalú tűréshatár, amely egy n méretű mintából vett eloszlás legalább β arányát tartalmazza, az x(u) rendezési statisztika. Az u indexet a következőképpen számítjuk ki:
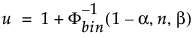
ahol Φ-1bin(1-α, n, β) a binomiális eloszlás (1 – α)-dik kvantora n próbával és β valószínűséggel.
A tényleges megbízhatósági szint kiszámítása a következőképpen történik: Φbin(u-1, n, β), ahol Φbin(x, n, β) annak a valószínűsége, hogy a binomiális eloszlású véletlen változó n próbával és β siker valószínűséggel kisebb vagy egyenlő x-szel.
Megjegyezzük, hogy a felső egyoldalú eloszlás nélküli toleranciaintervallum kiszámításához az n mintaméretnek legalább akkorának kell lennie, mint 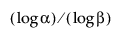 .
.
Kétoldalú toleranciaintervallum
A 100(1 – α)%-os kétoldalú toleranciaintervallumot, amely az n méretű mintából vett eloszlás legalább β arányát tartalmazza, a következőképpen számítjuk ki:
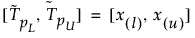
ahol x(i) az i-edik rendű statisztika, l és u pedig a következőképpen számíthatók:
Legyen ν = n – Φ-1bin(1-α, n, β), ahol Φ-1bin(1-α, n, β) a binomiális eloszlás (1 – α)-dik kvantilisét jelenti n próbával és β siker valószínűséggel. Ha ν kisebb, mint 2, akkor a kétoldali eloszlás nélküli toleranciaintervallum nem számítható ki. Ha ν nagyobb vagy egyenlő 2-nél, akkor l = floor(ν/2) és u = floor(n + 1 – ν/2).
A tényleges megbízhatósági szint kiszámítása Φbin(u-l-1, n, β), ahol Φbin(x, n, β) annak a valószínűsége, hogy a binomiális eloszlású véletlen változó n próbával és β siker valószínűséggel kisebb vagy egyenlő x-nél.
Megjegyezzük, hogy a kétoldali eloszlásmentes toleranciaintervallum kiszámításához az n mintaméretnek legalább akkorának kell lennie, mint a következő egyenletben szereplő n:

Az eloszlásmentes toleranciaintervallumokról bővebben lásd Meeker et al. (2017, 5.3. szakasz)
.