La terza legge postula che l’entropia di una sostanza è sempre finita e che si avvicina a una costante man mano che la temperatura si avvicina allo zero. Il valore di questa costante è indipendente dai valori di qualsiasi altra funzione di stato che caratterizza la sostanza. Per qualsiasi sostanza data, siamo liberi di assegnare un valore arbitrariamente selezionato al valore limite di temperatura zero. Tuttavia, non possiamo assegnare entropie di zero-temperatura arbitrarie a tutte le sostanze. L’insieme delle assegnazioni che facciamo deve essere coerente con i valori limite di zero-temperatura osservati sperimentalmente dei cambiamenti di entropia delle reazioni tra le diverse sostanze. Per sostanze perfettamente cristalline, queste entropie di reazione sono tutte zero. Possiamo soddisfare questa condizione assegnando un valore arbitrario all’entropia molare a temperatura zero di ogni elemento e stabilendo che l’entropia a temperatura zero di qualsiasi composto è la somma delle entropie a temperatura zero dei suoi elementi costituenti. Questo calcolo è molto semplificato se lasciamo che l’entropia a temperatura zero di ogni elemento sia zero. Questo è il contenuto essenziale della terza legge.
La dichiarazione di Lewis e Randall incorpora questa selezione dello stato di riferimento a zero entropia per le entropie, specificandolo come “uno stato cristallino” di ogni elemento a zero gradi. Di conseguenza, l’entropia di qualsiasi sostanza a zero gradi è maggiore o uguale a zero. Cioè, la dichiarazione di Lewis e Randall include una convenzione che fissa il valore limite a temperatura zero dell’entropia di qualsiasi sostanza. In questo senso, l’affermazione di Lewis e Randall fa una scelta essenzialmente arbitraria che non è una proprietà intrinseca della natura. Vediamo, tuttavia, che è una scelta estremamente conveniente.
Abbiamo discusso affermazioni alternative della prima e della seconda legge. Sono possibili anche alcune affermazioni alternative della terza legge. Consideriamo le seguenti:
È impossibile raggiungere una temperatura di zero assoluto.
Questa affermazione è più generale di quella di Lewis e Randall. Se consideriamo l’applicazione di questa affermazione alle temperature raggiungibili in processi che coinvolgono una singola sostanza, possiamo mostrare che essa implica, ed è implicata, dall’affermazione di Lewis e Randall.
Le proprietà della capacità termica, \(C_P\), giocano un ruolo centrale in questi argomenti. Abbiamo visto che \(C_P\) è una funzione della temperatura. Anche se non è utile farlo, possiamo applicare la relazione di definizione di \(C_P\) a una sostanza che subisce una transizione di fase e trovare \(C_P=infty\). Se pensiamo a una sostanza la cui capacità termica è inferiore a zero, incontriamo una contraddizione delle nostre idee di base su calore e temperatura: Se \(q>0\) e \({q}/{\Delta T}<0\), dobbiamo avere \(\Delta T<0\); cioè, il riscaldamento della sostanza fa diminuire la sua temperatura. In breve, la teoria che abbiamo sviluppato incorpora premesse che richiedono \(C_P>0\) per qualsiasi sistema su cui possiamo fare misurazioni.
Caratterizziamo un sistema a sostanza pura per la sua pressione e temperatura e consideriamo processi reversibili a pressione costante in cui è possibile solo il lavoro pressione-volume. Allora \({sinistra({parziale S}/{parziale T}destra)}P={C_P}/{T}}) e \(dS={C_PdT}/{T}). Ora vogliamo mostrare: la stipulazione di Lewis e Randall che l’entropia è sempre finita richiede che la capacità termica vada a zero quando la temperatura va a zero. (Dato che stiamo per mostrare che la terza legge proibisce misurazioni allo zero assoluto, questa conclusione è coerente con la nostra conclusione del paragrafo precedente). Che la capacità termica vada a zero quando la temperatura va a zero è evidente da \(S={C_PdT}/{T}.\) Se \(C_P\) non va a zero quando la temperatura va a zero, \(dS\) diventa arbitrariamente grande quando la temperatura va a zero, il che contraddice la dichiarazione di Lewis e Randall.
Per sviluppare più esplicitamente questo risultato, lasciamo che le capacità termiche alle temperature \(T\) e zero siano rispettivamente \(C_P\left(T\right)\) e \(C_P\left(0\right)\). Siccome \C_P\sinistra(T\destra)>0\) per qualsiasi \(T\ >0\), abbiamo \Sinistra(T\destra)-Sinistra(T^*destra)>0\) per qualsiasi \T>T^*>0\). Poiché l’entropia è sempre finita, \(\infty >Sinistra(T\destra)-Sinistra(T^*\destra)>0\), in modo che
\}>0\]
e
per temperature vicine allo zero, possiamo espandere la capacità termica, con una precisione arbitraria, come una serie di Taylor polinomiale in \(T\):
Le disuguaglianze diventano
La condizione a sinistra richiede \(C_P\left(0\right)=0\).
Potremmo vedere la terza legge come un’affermazione sulle capacità termiche delle sostanze pure. Non solo deduciamo che \(C_P>0\) per tutti i \(T>0\), ma anche che
\
Più in generale, possiamo dedurre affermazioni corrispondenti per sistemi chiusi reversibili che non sono sostanze pure: \(\sinistra(\parziale H)/destra)}P>0\) per tutti \(T>0\), e \(\mathop{mathrm{lim}_{T a 0} T^{-1}{sinistra(\parziale H}/{parziale T}destra)}_P=0\). (Le entropie a temperatura zero di tali sistemi non sono zero, comunque.) Nella discussione che segue, descriviamo il sistema come una sostanza pura. Possiamo fare essenzialmente gli stessi ragionamenti per qualsiasi sistema; dobbiamo solo sostituire \(C_P\) con \(\sinistra(\parziale H}/{parziale T}}destra)}_P\). L’affermazione di Lewis e Randall afferma che l’entropia va ad una costante allo zero assoluto, indipendentemente dai valori di qualsiasi altra funzione termodinamica. Ne segue che l’entropia a zero gradi è indipendente dal valore della pressione. Per due pressioni qualsiasi, \(P_1\) e \(P_2\), abbiamo \(S\left(P_2,0\right)-S\left(P_1,0\right)=0\). Lasciando \({P=P}_1\) e \(P_2=P+Delta P\) e, abbiamo
\
per qualsiasi \(\Delta P\). Quindi, abbiamo
Nel capitolo 10, troviamo \(\sinistra(\parziale S}/{parziale P}destra)}_T=-{sinistra(\parziale V}/{parziale T}destra)}_P\), quindi sia l’entropia che il volume si avvicinano asintoticamente ai loro valori a temperatura zero.
Quando diciamo che lo zero assoluto è irraggiungibile, intendiamo che nessun sistema può subire alcun cambiamento in cui la sua temperatura finale sia zero. Per vedere perché lo zero assoluto deve essere irraggiungibile, consideriamo i processi che possono diminuire la temperatura di un sistema. In generale, abbiamo serbatoi di calore disponibili a varie temperature. Possiamo scegliere il serbatoio disponibile la cui temperatura è più bassa, e portare il sistema a questa temperatura per semplice contatto termico. Questo è molto banale; chiaramente, la sfida è diminuire ulteriormente la temperatura. Per farlo, dobbiamo effettuare qualche altro cambiamento. Qualunque sia questo cambiamento, non può essere aiutato da uno scambio di calore con l’ambiente circostante. Una volta che abbiamo portato il sistema alla temperatura della porzione più fredda disponibile dell’ambiente, qualsiasi ulteriore scambio di calore con l’ambiente può essere solo controproducente. Concludiamo che qualsiasi processo adatto al nostro scopo deve essere adiabatico. Poiché un processo adiabatico non scambia calore con l’ambiente, \(\Delta \hat{S}=0\).
Il processo deve anche essere un processo possibile, in modo che \(\Delta S+\Delta \hat{S}ge 0\), e poiché è adiabatico, \(\Delta S\ge 0\). Consideriamo un processo reversibile e un processo irreversibile in cui lo stesso sistema passa dallo stato specificato da \(P_1\) e \(T_1\) a un secondo stato in cui la pressione è \(P_2\). Le temperature finali e i cambiamenti di entropia di questi processi sono diversi. Per il processo reversibile, \(\Delta S=0\); designiamo la temperatura finale come \(T_2\). Per il processo irreversibile, \(\Delta S>0\); designiamo la temperatura finale come \(T^*_2\). Come risulta, la variazione di temperatura è minore per il processo irreversibile che per il processo reversibile; cioè, \(T_2-T_1<t^*_2-t_1\)>. Equivalentemente, il processo reversibile raggiunge una temperatura inferiore: \({T_2<t}^*_2\)>. Da
possiamo calcolare le variazioni di entropia per questi processi. Per il processo reversibile, calcoliamo \
Per fare questo, calcoliamo prima
per la trasformazione isoterma reversibile dallo stato \(P_1\), \(T_1\) allo stato specificato da \(P_2\) e \(T_1\). Per questo passo, \(dT\) è zero, e quindi
Calcoliamo quindi
per la trasformazione reversibile isobara dallo stato \(P_2\), \(T_1\) allo stato \(P_2\), \(T_2\). Per questa trasformazione, \dP\ è zero, e
Quindi,
Perché \(\Delta S^{rev}=0\), il processo reversibile è unico; cioè, dati \(P_1\), \(T_1\), e \(P_2\), la temperatura finale del sistema è determinata. Troviamo \(T_2\) da
Per capire la variazione di entropia per il processo irreversibile, notiamo prima che ci sono un numero infinito di tali processi. Non c’è nulla di unico nella temperatura finale. Dati \(P_1\), \(T_1\), e \(P_2\), la temperatura finale, \(T^*_2\), può avere qualsiasi valore coerente con le proprietà della sostanza. Per specificare un particolare processo irreversibile, dobbiamo specificare tutte e quattro le quantità \(P_1\), \(T_1\), \(P_2\), e \(T^*_2\). Avendo fatto questo, tuttavia, possiamo calcolare la variazione di entropia per il processo irreversibile,
calcolando le variazioni di entropia mentre portiamo reversibilmente il sistema lungo il percorso isotermo a due passi da \(P_1\), \(T_1\) a \(P_2\), \(T_1\) e poi lungo il percorso isobarico da \(P_2\), \(T_1\) a \(P_2\), \(T^*_2\). Il calcolo di \(\Delta S^{irrev}\ per questo percorso reversibile da \(P_1\), \(T_1\) a \(P_2\), \(T^*_2\) utilizza la stessa logica del calcolo, nel paragrafo precedente, di \(\Delta S\) per il percorso reversibile da \(P_1\), \(T_1\) a \(P_2\), \(T_2\). La differenza è che \(T^*_2\) sostituisce \(T_2\) come limite superiore nell’integrale di temperatura. L’integrale di pressione è lo stesso. Si ha
Da \(\Delta S^{irrev}>\Delta S^{rev}\), si ha
Siccome gli integrali sono uguali e positivi, segue che \(T^*_2>T_2\), come asserito sopra.
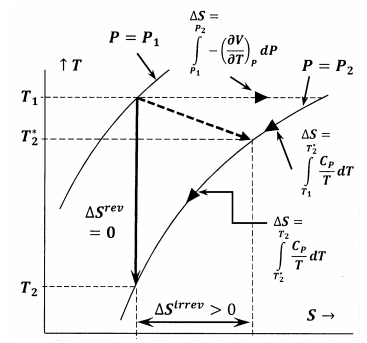
La figura 6 mostra le relazioni tra le varie quantità discusse in questo argomento. In primo luogo, la figura 6 mostra un grafico di due isobare del sistema nello spazio temperatura-entropia. Cioè, la linea etichettata \(P=P_1\) rappresenta l’insieme dei punti di temperatura-entropia in cui il sistema in equilibrio ha pressione \(P_1\); la linea etichettata \(P=P_2\), rappresenta le posizioni di equilibrio alla pressione \(P_2\). Altre linee in questo schizzo rappresentano percorsi lungo i quali il sistema può subire cambiamenti reversibili a entropia costante o a temperatura costante. La linea tratteggiata rappresenta il processo irreversibile in cui il sistema passa dallo stato specificato da \(P_1\), \(T_1\) allo stato specificato da \(P_2\), \(T^*_2\). Questa linea è tratteggiata per rappresentare il fatto che la temperatura del sistema può non essere ben definita durante il processo irreversibile.
Il raffreddamento efficace può essere ottenuto usando cambiamenti di pressione se il sistema è un gas. Tuttavia, per i liquidi e i solidi, \(\sinistra(\V parziale}/{T parziale} destra)}_P\) è piccolo; di conseguenza, il cambiamento di temperatura per un cambiamento di pressione reversibile è anche piccolo. A temperature vicine allo zero assoluto, quasi tutte le sostanze sono solide; per ottenere un raffreddamento efficace dobbiamo cambiare una variabile termodinamica per la quale il coefficiente di temperatura di un solido è il più grande possibile. Per considerare il problema generale di diminuire la temperatura di un sistema variando qualcosa di diverso dalla pressione, dobbiamo considerare un sistema in cui sia possibile qualche forma di lavoro non-pressione-volume. Un tale sistema è soggetto a una forza addizionale, e la sua energia cambia al variare di questa forza.
Demagnetizzazione adiabatica
Il metodo pratico con cui si ottengono temperature estremamente basse è chiamato smagnetizzazione adiabatica. Questo metodo sfrutta le proprietà dei solidi paramagnetici. In tali solidi, gli elettroni spaiati localizzati sui singoli atomi danno origine a un momento magnetico. La meccanica quantistica porta a conclusioni importanti sull’interazione tra questi momenti magnetici e un campo magnetico applicato: In un campo magnetico applicato, il momento magnetico di un singolo atomo è quantizzato. Nel caso più semplice, può essere allineato solo in due direzioni; deve essere parallelo o antiparallelo al campo magnetico applicato. Quando il momento magnetico di un atomo è parallelo al campo magnetico, l’energia del sistema è minore di quando l’allineamento è antiparallelo. Il campo magnetico applicato esercita una forza sui momenti magnetici associati ai singoli atomi. L’energia del sistema dipende dalla grandezza del campo magnetico applicato.
Piuttosto che concentrarci sul caso particolare della smagnetizzazione adiabatica, consideriamo i cambiamenti di energia e di entropia associati ai cambiamenti in un potenziale generalizzato, \({mathit{\Phi}}_{\theta }), e il suo spostamento generalizzato, \(\theta\). (Per la smagnetizzazione adiabatica, \(\theta\) sarebbe il campo magnetico applicato). Tre variabili sono necessarie per descrivere i cambiamenti reversibili in questo sistema. Possiamo esprimere l’energia e l’entropia come funzioni di temperatura, pressione, e \(\theta\):
\(E=E=Sinistra(T,P,\theta \destra)\) e \(S=Sinistra(T,P,\theta \destra)\). Il differenziale totale dell’entropia include un termine che specifica la dipendenza dell’entropia da \(\theta\). Abbiamo
dove scriviamo \(C\left(T,P,\theta \right)\) per sottolineare che i nostri scopi attuali richiedono ora di misurare la capacità termica a pressione costante e \theta\ costante.
Per pressione costante, P, e spostamento costante, \(\theta\), l’entropia dipende dalla temperatura come
Il postulato che l’entropia sia finita a qualsiasi temperatura implica che la capacità termica dipendente dalla pressione e dalla \theta\ diventa zero allo zero assoluto. Cioè, allo zero assoluto, la capacità termica svanisce qualunque siano i valori di P e \theta\. Il ragionamento è esattamente lo stesso di prima. Prima, abbiamo scritto \(C_P\sinistra(0\destra)=0\); per il presente caso generalizzato, scriviamo \(C\sinistra(0,P,\theta \destra)=0\).
Similmente, dal postulato che l’entropia va ad una costante allo zero assoluto per tutti i valori delle altre variabili termodinamiche, segue che, per due pressioni qualsiasi \(P_1\) e \(P_2\), e per due valori qualsiasi dello spostamento generalizzato,
e quindi che
e
vogliamo considerare un processo in cui un sistema passa dalla più bassa temperatura disponibile nell’ambiente ad una temperatura ancora più bassa. Per minimizzare la temperatura finale, questo processo deve svolgersi adiabaticamente. Deve anche essere un processo possibile, in modo che \(dS\ge 0\). Per semplicità, supponiamo ora di effettuare questo processo ad una pressione costante, \(P\), e che il sistema passi dallo stato specificato da \(P\), \(T_1\), \({\theta }_1\) allo stato specificato da \(P\), \(T_2\), \({\theta }_2\) dove \(T_1>T_2\). Le entropie di questi due stati sono
e \
La variazione di entropia per questo processo è
\
Ora, supponiamo che la temperatura finale sia zero; cioè \(T_2=0\), così che
segue che \
dove la disuguaglianza a destra segue dal fatto che \(C\left(T,P,{\theta }_1\right)>0\). Quindi, segue che
\
che contraddice l’affermazione di Lewis e Randall della terza legge. L’assunzione che il sistema possa raggiungere lo zero assoluto porta a una contraddizione dell’enunciato di Lewis e Randall della terza legge. Pertanto, se l’affermazione di Lewis e Randall è vera, lo zero assoluto è irraggiungibile.
Si applica anche il contrario; cioè, dalla proposizione che lo zero assoluto è irraggiungibile, possiamo dimostrare che l’affermazione di Lewis e Randall è vera. Per fare ciò, riorganizziamo l’equazione precedente per \(\Delta S\),
\
Se ora assumiamo che l’affermazione di Lewis e Randall sia falsa, l’espressione sulla destra può essere minore o uguale a zero. L’integrale a sinistra può quindi essere zero, nel qual caso il sistema può raggiungere lo zero assoluto. Se l’affermazione di Lewis e Randall è falsa, è vero che il sistema può raggiungere lo zero assoluto. Pertanto: Se il sistema non può raggiungere lo zero assoluto, l’affermazione di Lewis e Randall è vera.
Le figure 7 e 8 rappresentano queste idee usando i diagrammi di contorno nello spazio temperatura-entropia. Ogni figura mostra due curve di livello. Una di queste linee di contorno è un insieme di valori di temperatura ed entropia lungo i quali la pressione è costante a \(P\) e \(\theta\) è costante a \({\theta\_1\). L’altra curva di livello è un insieme di valori di temperatura ed entropia lungo i quali la pressione è costante a \(P\) e \(\theta\) è costante a \({\theta }_2\). La pendenza di una curva di livello è
Perché la capacità termica è sempre positiva, questa pendenza è sempre positiva.
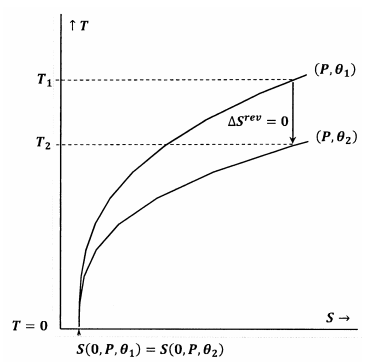
Nella figura 7, l’enunciato di Lewis e Randall è soddisfatto. Quando la temperatura va a zero, le linee di contorno si incontrano allo stesso valore dell’entropia; questi contorni soddisfano la relazione
Un percorso adiabatico (verticale) dal contorno per \(P\) e \({\theta }_1\) incontra il contorno per \(P\) e \({\theta }_2\) ad una temperatura positiva, \(T_2>0\). Poiché questo è evidentemente vero per qualsiasi \(P\) e qualsiasi \({\theta }_2\), lo stato finale per qualsiasi processo adiabatico avrà \(T_2>0\). Poiché la dichiarazione di Lewis e Randall è soddisfatta, il sistema non può raggiungere lo zero assoluto, e viceversa.
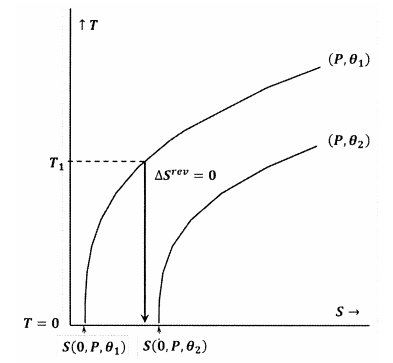
Nella figura 8, l’enunciato di Lewis e Randall è violato, perché abbiamo \(S\sinistra(0,P,{\theta }_1\right)\). In questo caso, un processo adiabatico iniziato da una temperatura iniziale abbastanza bassa, \(T_1\), raggiungerà lo zero assoluto senza intersecare il contorno per la costante \(P\) e \({\theta }_2\). Poiché la dichiarazione di Lewis e Randal è violata, il sistema può raggiungere lo zero assoluto, e viceversa.