Convoluzioni 1D e 3D spiegate con… MS Excel!

Abbiamo iniziato con le Convoluzioni 2D nel primo post perché le convoluzioni hanno guadagnato una significativa popolarità dopo i successi nel campo della Computer Vision. Dal momento che i compiti in questo campo usano le immagini come input, e le immagini naturali di solito hanno modelli lungo due dimensioni spaziali (di altezza e larghezza), è più comune vedere esempi di Convoluzioni 2D che di Convoluzioni 1D e 3D.

Più recentemente, però, c’è stato un enorme numero di successi nell’applicare le convoluzioni anche ai compiti di elaborazione del linguaggio naturale. Poiché i compiti in questo dominio usano il testo come input, e il testo ha modelli lungo una singola dimensione spaziale (cioè il tempo), le convoluzioni 1D sono un’ottima soluzione! Possiamo usarle come alternative più efficienti alle tradizionali reti neurali ricorrenti (RNN) come LSTM e GRU. A differenza delle RNN, possono essere eseguite in parallelo per calcoli davvero veloci.

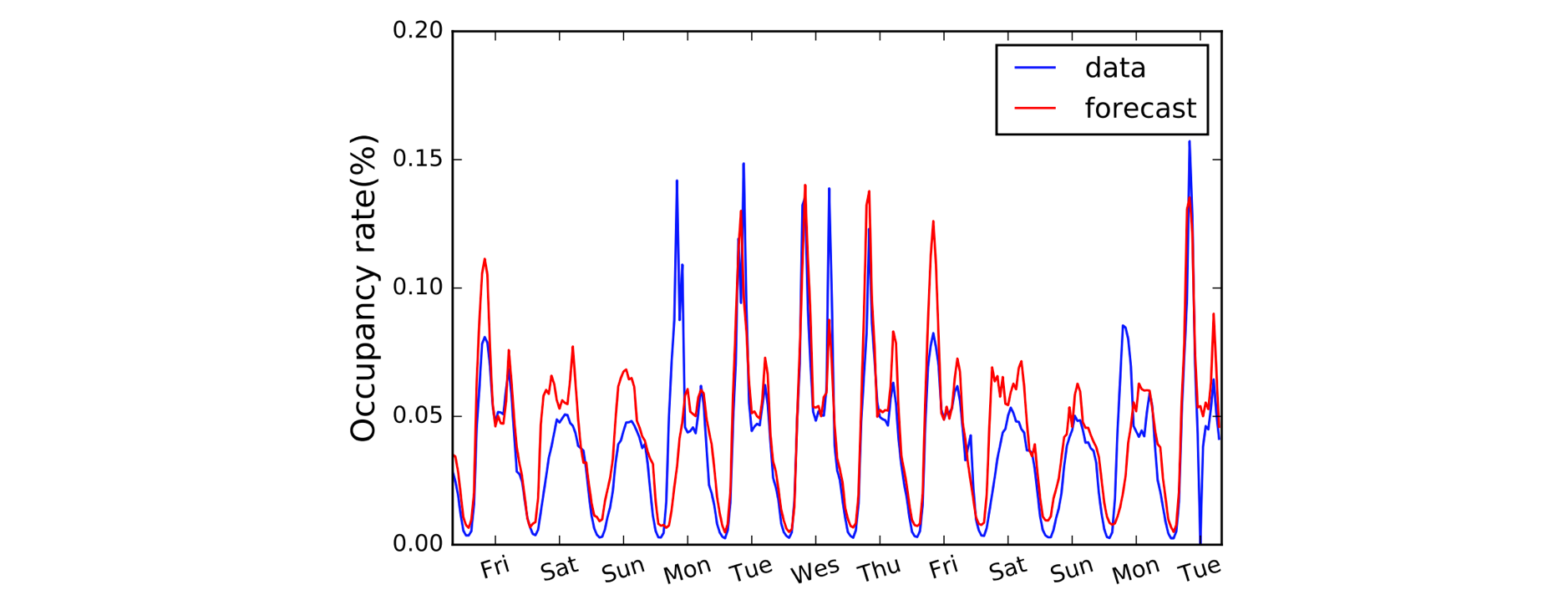
Un altro dominio che beneficia delle Convoluzioni 1D è la modellazione delle serie temporali. Come prima, abbiamo una singola dimensione spaziale sui nostri dati di input (cioè il tempo), e vogliamo cogliere i modelli su periodi di tempo. Spesso chiamiamo questo tipo di dati “sequenziali” perché possono essere visti come una sequenza di valori. E la dimensione spaziale spesso la chiamiamo dimensione ‘temporale’. Anche l’uso di convoluzioni 1D prima delle RNN è abbastanza comune: il modello LSTNet ne è un esempio e le sue previsioni per la previsione del traffico sono mostrate qui sotto.

A, B, C. È facile come (1,3,3) punto (2,0,1) = 5.

Chiarite le convenzioni di denominazione, diamo ora uno sguardo più da vicino all’aritmetica. Siamo fortunati perché le Convoluzioni 1D sono in realtà solo una versione semplificata della Convoluzione 2D!

Lavorando attraverso il calcolo di un singolo valore di uscita, possiamo applicare il nostro kernel di dimensione 3 alla regione di dimensioni equivalenti sul lato sinistro della nostra matrice di ingresso. Calcoliamo il ‘prodotto di punti’ della regione di input e del kernel, che per ricapitolare è solo il prodotto elemento-saggio (cioè moltiplicare le coppie di colori) seguito da una somma globale per ottenere un singolo valore. Quindi in questo caso:

(1*2) + (3*0) + (3*1) = 5

Applichiamo la stessa operazione (con lo stesso kernel) alle altre regioni della matrice di input per ottenere la matrice di output completa di (5,6,7,2); cioè facciamo scorrere il kernel su tutta la matrice di input. A differenza delle Convoluzioni 2D, dove facciamo scorrere il kernel in due direzioni, per le Convoluzioni 1D facciamo scorrere il kernel in una sola direzione; sinistra/destra in questo diagramma.

Avanzate: una Convoluzione 1D non è la stessa di una Convoluzione 2D 1×1.

Codificare le cose

Inaspettatamente, abbiamo bisogno di un blocco Conv1D in Gluon per la nostra Convoluzione 1D. Definiamo la forma del kernel come 3, e poiché stiamo lavorando con un solo kernel in questo esempio, specificheremo channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Possiamo ora passare il nostro input nel blocco conv usando un kernel predefinito.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

Cosa cambia con padding, stride e dilatazione?

Abbiamo visto l’effetto di padding, stride e dilatazione nell’ultimo post sulle Convoluzioni 2D, ed è molto simile per le Convoluzioni 1D. Con il padding, questa volta lo facciamo solo lungo una singola dimensione (la dimensione temporale). Il nostro diagramma rappresenta il tempo attraverso l’asse orizzontale, quindi imbottiamo a sinistra e a destra dei dati di input (e non sopra e sotto come nell’esempio della Convoluzione 2D). Con lo stride e la dilatazione, li applichiamo solo lungo la dimensione temporale. Quindi un esempio con padding e stride sarebbe il seguente:

Aggiungiamo due argomenti aggiuntivi nel codice: padding=1 e strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Avanzato: le dimensioni dei dati di input devono essere conformi a un particolare ordine chiamato layout. Per default la convoluzione 1D si aspetta di essere applicata a dati di input del formato ‘NCW’, cioè dimensione del lotto (N) * canali (C) * larghezza/tempo (W). E per le convoluzioni 2D il default è NCHW, cioè dimensione del lotto (N) * canali (C) * altezza (H) * larghezza (W). Controlla l’argomento layout di Conv1D e Conv2D.