Gruppo Abeliano | CDhistory

Un gruppo abeliano è un gruppo in cui gli elementi sono commutati (cioè, per tutti gli elementi e ). I gruppi abeliani corrispondono quindi a gruppi con tabelle di moltiplicazione simmetriche.

Tutti i gruppi ciclici sono abeliani, ma un gruppo abeliano non è necessariamente ciclico. Tutti i sottogruppi di un gruppo abeliano sono normali. In un gruppo abeliano, ogni elemento è in una classe di coniugazione da solo, e la tabella dei caratteri coinvolge potenze di un singolo elemento noto come generatore di gruppo.

Nel linguaggio Wolfram, la funzione AbelianGroup rappresenta il prodotto diretto dei gruppi ciclici di grado , , ….

Nessuna formula generale è nota per dare il numero di gruppi finiti non isomorfi di un dato ordine di gruppo. Tuttavia, il numero di gruppi finiti abeliani nonisomorfi di qualsiasi ordine di gruppo dato è dato scrivendo come

(1)

dove i sono fattori primi distinti, allora

(2)

dove è la funzione di partizione, che è implementata nel linguaggio Wolfram come FiniteAbelianGroupCount. I valori di per , 2, … sono 1, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, … (OEIS A000688).

I più piccoli ordini per cui , 2, 3, … esistono gruppi abeliani non isomorfi sono 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), dove 0 denota un numero impossibile (cioè, non un prodotto di numeri di partizione) di gruppi abeliani non isomorfi. I valori “mancanti” sono 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). I numeri incrementali dei gruppi abeliani in funzione dell’ordine sono 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), che si verificano per gli ordini 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

Il teorema della decomposizione di Kronecker afferma che ogni gruppo abeliano finito può essere scritto come un prodotto diretto di gruppi ciclici di ordine di gruppo a potenza prima. Se l’ordine di gruppo di un gruppo finito è un primo , allora esiste un solo gruppo abeliano di ordine (denotato ) e nessun gruppo non abeliano. Se l’ordine del gruppo è un primo al quadrato , allora esistono due gruppi abeliani (indicati come e . Se l’ordine del gruppo è un primo al cubo , allora ci sono tre gruppi abeliani (indicati come , , e ), e cinque gruppi totali. Se l’ordine è un prodotto di due primi e , allora esiste esattamente un gruppo abeliano di ordine (indicato come ).

Un altro risultato interessante è che se denota il numero di gruppi abeliani non isomorfi di ordine di gruppo , allora

(3)

dove è la funzione zeta di Riemann.

I numeri dei gruppi abeliani di ordine sono dati da 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) per , 2, …. Srinivasan (1973) ha anche dimostrato che

(4)

dove

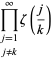			(5)
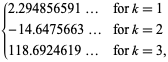			(6)

(OEIS A021002, A084892, e A084893) e è ancora la funzione zeta di Riemann. Si noti che Richert (1952) ha dato erroneamente . Le somme possono anche essere scritte nelle forme esplicite