Guarda gli articoli recenti

Abstract

La luce viaggia nel vuoto alla velocità c indipendentemente dal moto della sorgente luminosa o da quello del quadro di riferimento di un osservatore. Di conseguenza, è necessario un certo tempo perché la luce viaggi da una sorgente luminosa a un osservatore nello spazio, in modo tale che l’emissione di luce e l’osservazione della luce emessa non siano simultanee. Sulla base di queste considerazioni, viene proposto un metodo per misurare la velocità assoluta di un osservatore, che potrebbe essere utilizzato per determinare lo stato di moto di un veicolo spaziale dall’interno di una cabina chiusa. In questo studio viene anche introdotta una nuova spiegazione della trasformazione di Lorentz.

Parole chiave

sistema di coordinate, sistema di riferimento, movimento, velocità assoluta, relatività, trasformazione di Lorentz, tempo, spazio, osservatore, sorgente luminosa
La seguente analisi presenta un approccio pratico per misurare la velocità assoluta di un osservatore, che potrebbe essere usato per determinare lo stato di moto di un veicolo spaziale dall’interno di una cabina chiusa. Il concetto di velocità assoluta si riferisce generalmente a una velocità uniforme standard dei vari oggetti di un sistema fisico rispetto a uno spazio immobile postulato che esiste indipendentemente dagli oggetti fisici in esso contenuti (cioè, uno spazio assoluto). Qui presentiamo un approccio basato sulla cinematica rigida per dimostrare che la velocità assoluta di un osservatore può essere determinata dal fatto che la luce viaggia attraverso il vuoto alla velocità c indipendentemente dal moto della sorgente luminosa o da quello del quadro di riferimento dell’osservatore. Di conseguenza, è necessario un certo tempo perché la luce viaggi da una sorgente luminosa a un osservatore nello spazio, in modo tale che l’emissione di luce e l’osservazione della luce emessa non siano simultanee.
Nell’analisi proposta, forniamo prima le seguenti convenzioni per i sistemi di coordinate in esame. Assumiamo un sistema di coordinate cartesiane composto da tre assi perpendicolari a due a due originati dal punto (0,0,0), dove qualsiasi punto P nello spazio può essere definito dalle sue coordinate lungo gli assi x, y e z, rappresentati da una coppia ordinata di numeri reali (x,y,z). Si suppone che un sistema di riferimento inerziale S sia rappresentato da un sistema di coordinate spaziali rettangolari (x,y,z) la cui origine è O. Una serie di orologi standard (indicati come orologi S) sono situati in punti stazionari in S. Gli orologi S sono reciprocamente calibrati (cioè, forniscono letture equivalenti allo stesso istante di tempo) sulla base della trasmissione e ricezione di un segnale luminoso. In particolare, al tempo tA, un raggio di luce viene proiettato dall’orologio A all’orologio B, che viene poi riflesso al tempo tB dall’orologio B verso l’orologio A, e arriva all’orologio A al tempo tA’. Se , i due orologi sono calibrati. Per qualsiasi evento situato alle coordinate x,y,z, la sua coordinata temporale t è data dalla lettura dell’orologio S relativo all’evento. Allo stesso modo, un altro sistema di riferimento inerziale S’ è stabilito sulla base di un secondo sistema di coordinate rettangolari spaziali (x’,y’,z’) la cui origine è O’, e un’altra serie di orologi standard calibrati reciprocamente (orologi S’) sono situati in punti stazionari nel sistema di riferimento S’. Per qualsiasi evento situato alle coordinate x’,y’,z’, la sua coordinata temporale t’ è data dalla lettura dell’orologio S’ relativo all’evento.
Poiché le rispettive origini delle coordinate spaziali e temporali, così come le direzioni degli assi delle coordinate possono essere scelte arbitrariamente in larga misura, le relazioni tra S e S’ utilizzate qui si basano sulle seguenti convenzioni, che sono state applicate per semplicità.
(1) In un particolare istante nel tempo, le origini e gli assi delle coordinate dei due sistemi sono sovrapposti, e gli orologi situati rispettivamente a O e O’ sono messi a zero, cioè, .
(2) Gli assi x e x’ sono coincidenti nella direzione del moto relativo di S e S’; quindi, x e x’ sono sempre coincidenti, mentre y e y’, così come z e z’ sono paralleli.
(3) S’ si muove lungo la direzione +x di S.
L’analisi proposta si basa sul principio fondamentale che la luce nel vuoto viaggia a velocità costante c indipendentemente dal moto dell’osservatore o della sorgente luminosa. Così, qui definiamo la velocità assoluta U dell’osservatore, che si assume essere lineare e uniforme, come , dove f(φ) rappresenta una funzione della relazione geometrica tra la direzione di un segnale luminoso e la direzione di U, qui indicata come φ.
Nell’analisi proposta vengono fornite due nuove spiegazioni della relatività del tempo e della lunghezza, che differiscono dalle spiegazioni di Einstein (si veda “Sulla elettrodinamica dei corpi in movimento”). Queste spiegazioni sono introdotte nelle sezioni seguenti.

La relatività del tempo

A causa della velocità finita della luce, è necessario un certo tempo perché la luce viaggi da una sorgente luminosa a un osservatore nello spazio. Si può quindi dedurre che l’emissione della luce e l’osservazione della luce non possono essere simultanee. Sulla base della costanza della velocità della luce e delle condizioni illustrate nella figura 1, definiamo i seguenti fattori. Le posizioni di una sorgente luminosa e di un osservatore a , nel momento in cui la sorgente luminosa emette luce (indicata come evento R), sono date rispettivamente come A e H0. Durante il periodo di propagazione della luce da a , l’osservatore percorre una distanza U∙T dalla posizione H0 a H, dove l’osservatore riceve la luce emessa. Di conseguenza, definiamo come la distanza l tra la posizione dell’osservatore alla ricezione del segnale luminoso a e la posizione della sorgente luminosa quando emette luce a . A causa della costanza della velocità della luce, . La distanza è equivalente a U∙T. Infine, definiamo come la distanza l0 tra la posizione dell’osservatore a e la posizione della sorgente luminosa a . Qui, introduciamo una considerazione sulla posizione dell’osservatore a , che precedentemente si pensava non avesse alcun significato fisico. Se gli stati di moto dell’osservatore e della sorgente luminosa sono equivalenti, l0 è dato, così che U può essere calcolato attraverso le relazioni triangolari illustrate nella figura 1. Nel presente lavoro, il tempo di un evento è misurato utilizzando il seguente metodo. Sia l’osservatore che un orologio sono posti all’origine. Quando il segnale luminoso che rappresenta il verificarsi di un evento raggiunge l’osservatore, il tempo di arrivo della luce corrisponderà al tempo indicato dall’orologio. Il vantaggio della corrispondenza è che essa è sempre legata alla posizione dell’osservatore che impiega l’orologio. Come si vede nella figura 1, il punto spaziale O3 può essere definito in base alla posizione della sorgente luminosa quando emette luce a , e il punto spaziale O2 può essere definito in base alla posizione dell’osservatore quando riceve luce a . Tuttavia, il mezzo per definire il punto spaziale O1 in cui si trova l’osservatore quando la sorgente luminosa emette luce a non è ovvio. Per risolvere questo problema, si introducono i concetti di riposo assoluto (cioè ) e di moto assoluto (cioè ). Sostituiamo rispettivamente il singolo osservatore in movimento in H0 e H con due osservatori H1 e H2 a riposo nei punti spaziali O1 e O2, rispettivamente, mentre la sorgente luminosa A è a riposo nel punto spaziale O3. Ognuno degli osservatori e la sorgente luminosa impiegano orologi standard calibrati, e A emette un segnale luminoso a , indicato come evento R0. Quando l’osservatore H1 riceve il segnale luminoso che viaggia a c, la lettura dell’orologio è T0, e quando H2 lo riceve, la lettura è T. Come tale, le distanze e possono essere definite in base ai rispettivi tempi di viaggio del segnale luminoso come segue:
, (1)
e
. (2)
Secondo le relazioni triangolari mostrate nella figura 1, la trasformazione dell’evento R0 tra gli osservatori H1 e H2 è data come segue.
(3)
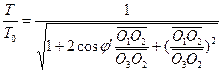(4)
Qui, è l’angolo tra la linea O3O1 e l’asse x, e è l’angolo tra la linea O3O2 e l’asse x.
Tornando ora alla condizione di un unico osservatore in movimento, assumiamo che, nel sistema S, sia l’osservatore H che la sorgente luminosa A impieghino un orologio standard calibrato. All’istante dell’evento R, la sorgente di luce A si trova nel punto spaziale O3 e l’osservatore H si trova in O1. L’istante in cui il segnale luminoso raggiunge il punto spaziale O1 corrisponde a una lettura dell’orologio S di T0. Quando l’osservatore H riceve il segnale luminoso, la lettura è T, e H si trova in O2.
Naturalmente, H non può osservare l’evento R nel punto O1. Per risolvere questo problema, un altro osservatore H- viene posto nel sistema S nel punto O1 corrispondente a , dove la posizione di H- viene impiegata per definire il punto spaziale O1. Quindi, la trasformazione dell’evento R tra gli osservatori H- e H può essere ottenuta attraverso l’equazione (3) come segue.
(5)
Quindi, le equazioni (3) e (4) possono essere riscritte come segue.
(6)
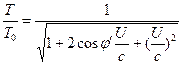(7)
e si osserva anche che, per , le equazioni (6) e (7) si semplificano come segue.
(8)
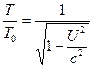(9)
Quindi, sulla base dell’analisi di cui sopra, un metodo semplice per determinare U può essere ottenuto dall’equazione (6), dato che (φ) è noto.
Per semplicità, si sceglie come quadro di riferimento una sorgente luminosa con uno stato di moto equivalente a quello degli osservatori. Un osservatore è posto al centro di una barra rigida rettilinea in moto lineare uniforme, e i segnali luminosi da diverse posizioni sulla barra arrivano all’osservatore in tempi diversi. L’osservatore rileva la deflessione della barra nella posizione dell’osservatore con un angolo di deflessione che può essere ottenuto dall’equazione (8).
Con questo metodo, lo stato di moto di un veicolo spaziale potrebbe essere determinato da una cabina chiusa.

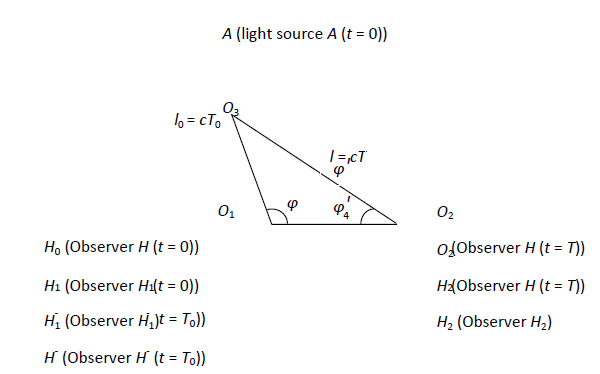
Figura 1: stati di moto dell’osservatore e della sorgente luminosa

La relatività della lunghezza

Nell’analisi precedente, sono state introdotte due lunghezze, cioè e . In questo caso, consideriamo la lunghezza di una barra che si assume essere una barra rigida stazionaria di lunghezza L all’interno del suo sistema di coordinate, per la quale L è misurata con un calibro personale stazionario, e dove l’asse della barra è coincidente con l’asse x di un sistema di coordinate che si muove con moto lineare uniforme lungo la direzione +x ad una velocità assoluta U. Si assume che L sia determinata dalle due operazioni definite di seguito.
(a) L’osservatore risiede nello stesso sistema di coordinate in movimento della barra e dell’asta, e L viene misurata sovrapponendo la barra e l’asta.
(b) Con l’aiuto di diversi orologi posizionati in coordinate stazionarie, che si muovono in sincronia, l’osservatore misura le posizioni delle due estremità della barra in coordinate stazionarie in un determinato momento t, e la distanza tra le due posizioni viene misurata con l’asta fissa. è la lunghezza calcolata dall’operazione (a), che viene qui indicata come la lunghezza della barra in coordinate mobili. è la lunghezza calcolata dall’operazione (b), che qui viene indicata come la lunghezza di una barra in movimento nella coordinata stazionaria. È ovvio che e sono diversi.
Assumiamo che, nel sistema S, l’osservatore H- sia nello stesso stato di moto di H. Allora, come mostrato nella figura 1, H- è nel punto O1 quando riceve il segnale luminoso a , e, contemporaneamente, l’osservatore H è nel punto O4. Quindi, t=0,04
è la distanza tra H- e H a , e
. (10)
è la distanza percorsa dall’osservatore H nell’intervallo da T0 a T, tale che
. (11)
è la distanza tra H- a e H a , tale che
. (12)
Come tale, si può dedurre la seguente espressione.
(13)
Prossimo, considereremo le trasformazioni di coordinate e di tempo tra due sistemi di coordinate in movimento, entrambi con una velocità lineare uniforme, che rappresenta una nuova spiegazione della trasformazione di Lorentz.
Assumendo che l’osservatore H (nel sistema S), l’osservatore H’ (nel sistema S’), e la sorgente di luce A” (nel sistema S”) impieghino tutti individualmente orologi standard calibrati e, al , la sorgente di luce A” emetta un segnale luminoso, indicato come evento R”. All’istante dell’evento R”, A” si trova nel punto O3, e gli osservatori H e H’ sono coincidenti. Quando l’osservatore H riceve il segnale luminoso, la lettura dell’orologio S è T, e H si trova nel punto O1. Quando l’osservatore H’ riceve il segnale luminoso, la lettura dell’orologio S’ è T’, e H’ si trova nel punto O2. Quindi, la trasformazione dell’evento R” tra gli osservatori H’ e H può essere calcolata dall’equazione (3), dove
. (14)
Qui, u è la velocità relativa tra gli osservatori H’ e H, che produce le seguenti trasformazioni.
(15)
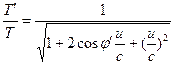(16)
Da , si possono derivare le seguenti relazioni:
. (17)
Quando e , l’equazione (16) si semplifica in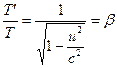
. (18)
Pertanto, le seguenti relazioni di trasformazione possono essere dedotte:
, (19)
, (20)
, (21)
. (22)
Inoltre, quando ,
, (23)
e
, (24)
, (25)
, (26)
. (27)