Intervalli di tolleranza
Questa sezione contiene dettagli statistici per intervalli di tolleranza unilaterali e bilaterali.
Intervalli basati sulla distribuzione normale
Intervallo unilaterale
L’intervallo unilaterale è calcolato come segue:
Limite inferiore = 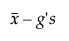
Limite superiore = 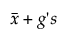
dove
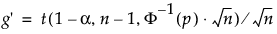
s è la deviazione standard
t è il quantile dalla noncentrale t
Φ-1 è il quantile normale standard
Intervallo a due lati
L’intervallo a due lati è calcolato come segue:
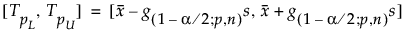
dove s è la deviazione standard e g(1-α/2; p,n) è una costante.
Per determinare g, considerare la frazione della popolazione catturata dall’intervallo di tolleranza. Tamhane e Dunlop (2000) danno questa frazione come segue:
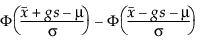
dove Φ indica la cdf (funzione di distribuzione cumulativa) normale standard.
Pertanto, g risolve la seguente equazione:
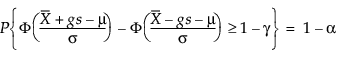
dove 1 – γ è la frazione di tutte le osservazioni future contenute nell’intervallo di tolleranza.a, J.1b, J.6a e J.6b di Meeker et al. (2017).
Intervalli non parametrici
Limite inferiore unilaterale
Il limite di tolleranza inferiore del 100(1 – α)% unilaterale per contenere almeno una proporzione β della distribuzione campionata da un campione di dimensione n è la statistica di ordine x(l). L’indice l è calcolato come segue:
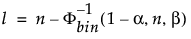
dove Φ-1bin(1-α, n, β) è il (1 – α)° quantile della distribuzione binomiale con n prove e probabilità di successo β.
Il livello di confidenza reale è calcolato come Φbin(n-l, n, β), dove Φbin(x, n, β) è la probabilità che una variabile casuale distribuita binomialmente con n prove e probabilità di successo β sia inferiore o uguale a x.
Nota che per calcolare un intervallo di tolleranza inferiore senza distribuzione unilaterale, la dimensione del campione n deve essere almeno grande come 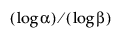 .
.
Limite superiore unilaterale
Il limite superiore di tolleranza unilaterale del 100(1 – α)% per contenere almeno una proporzione β della distribuzione campionata da un campione di dimensione n è la statistica di ordine x(u). L’indice u è calcolato come segue:
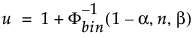
dove Φ-1bin(1-α, n, β) è il (1 – α)° quantile della distribuzione binomiale con n prove e probabilità di successo β.
Il livello di confidenza reale è calcolato come Φbin(u-1, n, β), dove Φbin(x, n, β) è la probabilità che una variabile casuale distribuita binomialmente con n prove e probabilità di successo β sia minore o uguale a x.
Nota che per calcolare un intervallo di tolleranza superiore senza distribuzione, la dimensione del campione n deve essere almeno grande come 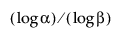 .
.
Intervallo a due lati
L’intervallo di tolleranza a due lati del 100(1 – α)% per contenere almeno una proporzione β della distribuzione campionata da un campione di dimensione n è calcolato come segue:
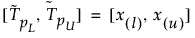
dove x(i) è l’iesimo ordine statistico e l e u sono calcolati come segue:
Lascia che ν = n – Φ-1bin(1-α, n, β), dove Φ-1bin(1-α, n, β) è il (1 – α)th quantile della distribuzione binomiale con n prove e probabilità di successo β. Se ν è inferiore a 2, non è possibile calcolare un intervallo di tolleranza a due lati senza distribuzione. Se ν è maggiore o uguale a 2, l = floor(ν/2) e u = floor(n + 1 – ν/2).
Il livello di confidenza effettivo è calcolato come Φbin(u-l-1, n, β), dove Φbin(x, n, β) è la probabilità di una variabile casuale distribuita binomialmente con n prove e probabilità di successo β inferiore o uguale a x.
Nota che per calcolare un intervallo di tolleranza senza distribuzione su due lati, la dimensione del campione n deve essere grande almeno quanto la n nella seguente equazione:

Per maggiori informazioni sugli intervalli di tolleranza senza distribuzione, vedi Meeker et al. (2017, sec. 5.3).