Ricostruzione 3D

In questa pratica, l’intenzione è quella di programmare la logica necessaria per permettere al robot kobuki di generare una ricostruzione 3D della scena che sta ricevendo attraverso le sue telecamere destra e sinistra.

Installazione

Installazione dell’infrastruttura generale della JdeRobot Robotics Academy.

Come eseguire la tua soluzione?

Naviga nella directory 3d_reconstruction

cd exercises/3d_reconstruction

Lancia Gazebo con il mondo kobuki_3d_reconstruction attraverso il comando

roslaunch ./launch/3d_reconstruction_ros.launch

Poi devi eseguire l’applicazione accademica, che incorporerà il tuo codice:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Come eseguire l’esercizio?

Per svolgere l’esercizio, devi modificare il file MyAlgorithm.py e inserire in esso il tuo codice, che ricostruisce i punti 3d dalle due viste stereo.

Dove inserire il codice?

Nel file MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Application Programming Interface

• self.getImage('left') – per ottenere l’immagine sinistra
• self.getImage('right') – per ottenere l’immagine destra
• self.point.PlotPoint(position, color) – per tracciare il punto nello strumento 3d

Navigazione dell’interfaccia grafica

Basata sul mouse: Tenere premuto e trascinare per muoversi nell’ambiente. Scorri per ingrandire o ridurre

Basato su tastiera: Tasti freccia per muoversi nell’ambiente. Tasti W e S per ingrandire o rimpicciolire

Teoria

Nella computer vision e nella computer grafica, la ricostruzione 3D è il processo di determinazione del profilo 3D di un oggetto, così come la conoscenza delle coordinate 3D di qualsiasi punto del profilo. La ricostruzione può essere realizzata come segue:

• Basato sull’hardware: L’approccio basato sull’hardware ci richiede di utilizzare l’hardware specifico per il compito di ricostruzione. L’uso della luce strutturata, del telemetro laser, del misuratore di profondità e dei metodi radiometrici sono alcuni esempi.

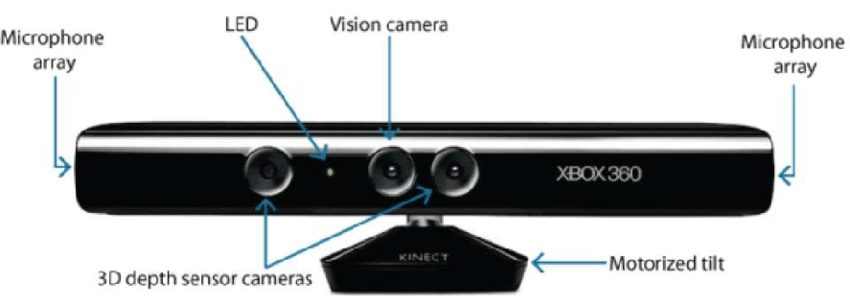
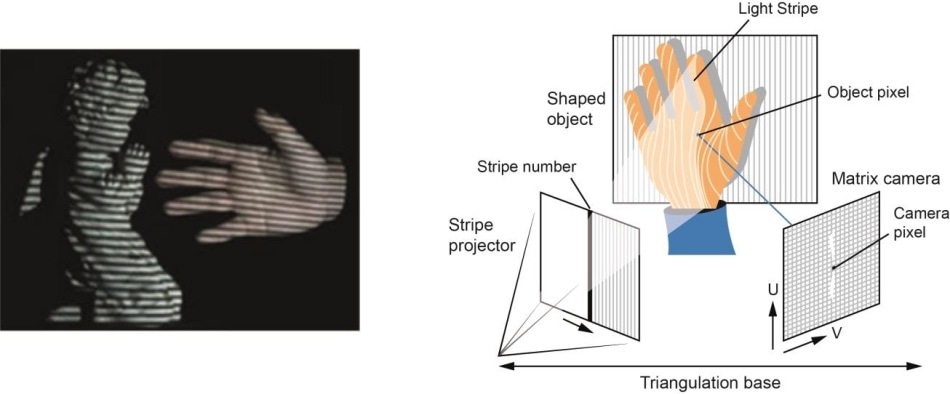
• Software Based: L’approccio basato sul software si basa sulle capacità di calcolo del computer per determinare le proprietà 3D dell’oggetto. La forma dall’ombreggiatura, la texture, la visione stereo e l’omografia sono alcuni buoni metodi.

In questo esercizio il nostro obiettivo principale è quello di effettuare la ricostruzione 3D utilizzando l’approccio basato sul software, in particolare la ricostruzione 3D della visione stereo.

Geometria epipolare

Quando due telecamere vedono una scena 3D da due posizioni diverse, ci sono una serie di relazioni geometriche tra i punti 3D e le loro proiezioni sulle immagini 2D che portano a vincoli tra i punti delle immagini. Lo studio di queste proprietà e vincoli è chiamato Geometrie Epipolari. L’immagine e la spiegazione che seguono possono generalizzare l’idea:

Supponiamo che un punto X nello spazio 3D sia ripreso in due viste, a x nella prima e x' nella seconda. Retroproiettando i raggi ai loro centri di camera attraverso i piani dell’immagine, otteniamo una superficie piana, indicata con π.

Supponendo ora che conosciamo solo x, possiamo chiedere come è costretto il punto corrispondente x'. Il piano π è determinato dalla linea di base (linea che collega i centri delle telecamere) e dalla semiretta definita da x. Da sopra, sappiamo che la semiretta corrispondente al punto sconosciuto x' giace in π, quindi il punto x' giace sulla linea di intersezione l' di π con il secondo piano dell’immagine. Questa linea è chiamata linea epipolare corrispondente a x. Questa relazione ci aiuta a ridurre lo spazio di ricerca del punto nell’immagine destra, da un piano a una linea. Alcune definizioni importanti da notare sono:

• L’epipolo è il punto di intersezione della linea che unisce i centri delle telecamere (la linea di base) con il piano dell’immagine.

• Un piano epipolare è un piano contenente la linea di base.

• Una linea epipolare è l’intersezione del piano epipolare con il piano dell’immagine.

Ricostruzione stereo

La ricostruzione stereo è un caso speciale della precedente ricostruzione 3d dove i due piani dell’immagine sono paralleli tra loro e ugualmente distanti dal punto 3d che vogliamo tracciare.

In questo caso la linea epipolare per entrambi i piani immagine sono uguali, e sono paralleli alla larghezza dei piani, semplificando meglio il nostro vincolo.

Algoritmo di ricostruzione 3D

L’algoritmo di ricostruzione consiste di 3 passi:

1. Rilevare i punti caratteristici in un piano dell’immagine
2. Rilevare il punto caratteristico corrispondente a quello trovato sopra
3. Triangolare il punto nello spazio 3d

Guardiamoli uno per uno

Rilevazione del punto caratteristico

La rilevazione del punto caratteristico è una vasta area di studio dove sono già studiati diversi algoritmi. Gli algoritmi Harris Corner Detection e Shi-Tomasi usano i valori autoctoni per ottenere un buon punto caratteristica. Ma il problema è che abbiamo bisogno di molti punti per la ricostruzione 3D, e questi algoritmi non saranno in grado di fornirci un numero così grande di punti caratteristici.

Perciò, usiamo i punti di bordo come punti caratteristici. Ci può essere un’ambiguità nella loro individuazione nella fase successiva dell’algoritmo. Ma, il nostro problema è risolto prendendo i bordi come punti caratteristici. Un rilevatore di bordi davvero fantastico è Canny Edge Detection Algorithm. L’algoritmo è abbastanza semplice e affidabile in termini di generazione dei bordi.

Estrazione dei punti caratteristici

L’uso del vincolo epipolare semplifica davvero la complessità temporale del nostro algoritmo. Per problemi generali di ricostruzione 3d, dobbiamo generare una linea epipolare per ogni punto in un fotogramma, e poi cercare in quello spazio campione il punto corrispondente nell’altro fotogramma. La generazione della linea epipolare è anche molto facile nel nostro caso, è solo l’iterpolazione della linea parallela dall’immagine sinistra al piano dell’immagine destra.

Controllare la corrispondenza tra le immagini coinvolge molti algoritmi, come la Somma delle differenze al quadrato o la Minimizzazione dell’energia. Senza andare molto in profondità, l’uso di un semplice filtro di correlazione è sufficiente anche per il nostro caso d’uso.

Triangolazione

La triangolazione in termini semplici è solo calcolare dove si troverà il punto 3d usando i due punti determinati nei piani dell’immagine.

In realtà, la posizione dei punti dell’immagine non può essere misurata esattamente. Per le telecamere generiche, ci possono essere distorsioni geometriche o fisiche. Pertanto, molta matematica sta dietro alla minimizzazione di questo errore e al calcolo della proiezione di punti 3d più accurata. Fai riferimento a questo link per un semplice modello.

Suggerimenti

Semplici suggerimenti forniti per aiutarti a risolvere l’esercizio 3d_reconstruction. La libreria OpenCV è usata ampiamente per questo esercizio.

Setup

Utilizzando l’API dell’esercizio, possiamo facilmente recuperare le immagini. Inoltre, dopo aver ottenuto le immagini, è una buona idea eseguire un filtraggio bilaterale sulle immagini, perché ci sono alcuni dettagli extra che non devono essere inclusi durante la ricostruzione 3D. Guarda le illustrazioni per gli effetti dell’esecuzione del filtraggio bilaterale.

Calcolo delle corrispondenze

OpenCV ha già dei filtri di correlazione integrati che possono essere chiamati attraverso matchTemplate(). Fate attenzione ai casi estremi come i bordi e gli angoli.

Una buona osservazione è che i punti a sinistra avranno corrispondenza nella parte sinistra e i punti a destra avranno corrispondenza nella parte destra. Usando questa osservazione, possiamo facilmente accelerare il calcolo delle corrispondenze.

Piastrellatura dei punti

La funzione manuale o basata su OpenCV triangulatePoints funziona bene per la triangolazione. Basta fare attenzione a tutte le forme e dimensioni della matrice mentre si eseguono le implementazioni algebriche.

Tenete a mente la differenza tra semplici coordinate 3D e coordinate 4D omogenee. Guardate questo video per i dettagli. Dividendo semplicemente il vettore 4d completo per la sua quarta coordinata si ottengono le coordinate 3d.

A causa delle diverse implementazioni degli utenti, l’utente potrebbe dover regolare la scala e l’offset dei punti triangolati per renderli visibili e rappresentabili nell’interfaccia GUI. Il ridimensionamento del vettore di coordinate 3D di un valore compreso tra 500 e 1000 funziona bene. Anche un offset da 0 a 8 funziona bene.

Illustrazioni