La procedura di sottrazione per l’eliminazione del PL è stata elaborata circa due decenni fa. Questa procedura non influisce sulle componenti ECG vicine alla frequenza PL. Questo studio teorico viene effettuato per la frequenza PL di base, ma le conclusioni sono valide anche per le sue armoniche e, di conseguenza, per una forma d’onda di interferenza arbitraria. L’efficienza della procedura non dipende dall’ampiezza dell’interferenza, a condizione che l’amplificatore non sia saturo. Inoltre, la procedura affronta con successo i cambiamenti di ampiezza e frequenza dell’interferenza. La procedura è stata continuamente migliorata nel corso degli anni, e implementata in migliaia di strumenti ECG e sistemi assistiti da computer. Approcci simili sono stati pubblicati anche da altri ricercatori.
- Principi
- Criterio lineare
- Compensazione delle variazioni di ampiezza del PL
- Filtraggio lineare
- Compensazione della variazione di frequenza PL
- Valutazione dell’efficienza della procedura
- Influenza del rumore EMG
- Soppressione delle interferenze nell’ECG ad alta risoluzione
- Caso di dispositivi alimentati a batteria e sistemi ECG computerizzati
- Adattamento automatico alla frequenza nominale PL
- Sviluppo della procedura teorica
Principi
La procedura di sottrazione è applicata originariamente con frequenza di campionamento f S, un multiplo di, e hardware sincronizzato con la frequenza PL f PL . La procedura consiste nei seguenti passi :
-
Segmenti ECG con banda di frequenza vicina allo zero sono continuamente rilevati usando un criterio appropriato. Sono chiamati segmenti lineari e si trovano principalmente negli intervalli PQ e TP, ma anche in parti rettilinee sufficientemente lunghe delle onde R e T.
-
I campioni di questi segmenti sono mediati in movimento, cioè sottoposti a un filtro a pettine di fase lineare con primo zero fissato a f PL . Così, i campioni filtrati non contengono interferenze.
-
Le ampiezze di interferenza, chiamate correzioni, sono calcolate per ciascuno dei campioni in fase, n, nel periodo PL, T PL , sottraendo i campioni filtrati da quelli corrispondenti del segnale ECG contaminato (originale).
-
L’insieme delle correzioni ottenute viene continuamente aggiornato nei segmenti lineari e utilizzato nei segmenti non lineari (di solito intorno ai complessi QRS e alle onde T ad alta ampiezza) per sottrarre l’interferenza dal segnale ECG originale.
Uno dei primi risultati ottenuti con il metodo della sottrazione è mostrato in Fig. 1 . L’interferenza è stata aggiunta a un segnale ECG simulato pulito per valutare gli errori e l’efficienza del metodo.
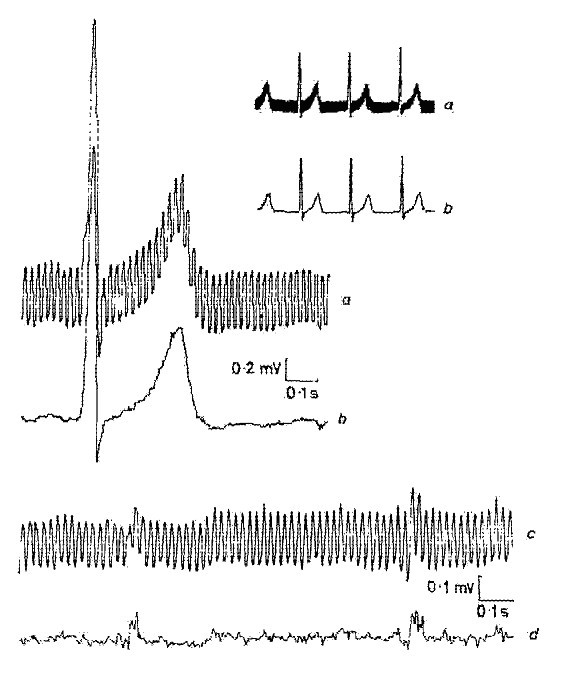
Uno dei primi risultati ottenuti dalla procedura di sottrazione.
Criterio lineare
Un criterio lineare, Cr, corrisponde solitamente alla seconda differenza del segnale (valutazione matematica della linearità). Il primo Cr è definito nel modo seguente. Sei prime differenze consecutive, FD i , sono calcolate usando campioni di segnale, X i , distanziati di un T PL :
FD i = X i+n – X i , per i = 1 … 6 (1)
L’interferenza PL nelle prime differenze è soppressa se n = f S /f PL . In questo caso n = 5, poiché la procedura è stata sviluppata inizialmente per f PL nominale = 50 Hz e f S = 250 Hz. Inoltre, i valori massimi FD max e minimi FD min sono presi per determinare Cr:
Cr = | FD max – FD min | <M, (2)
dove M è il valore di soglia.
I segmenti tipici lineari e non lineari sono mostrati in Fig. 2. Il segnale ECG reale (traccia a) è sovrapposto all’interferenza (traccia b). I segmenti lineari includono il segnale a bassa frequenza e le componenti di frequenza della linea elettrica. Uno spettro di frequenza approssimativo di tali segmenti lineari è mostrato in Fig. 3.

Segmenti tipici lineari e non lineari nel segnale ECG reale.
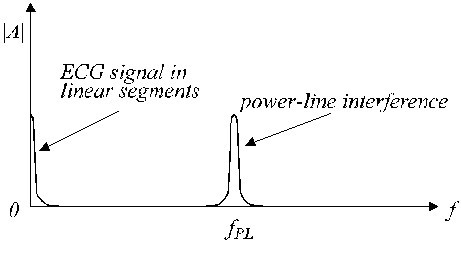
Spettro di frequenza approssimativo di un segmento lineare. Questo inconveniente è superato da Christov e Dotsinsky che usano un criterio modificato di due sole differenze successive.
Cr = | FDi+1- FD i | <M. (3)
Il primo campione, che non soddisfa l’equazione (3), è associato all’inizio di un segmento non lineare. Nella transizione da non lineare a lineare, l’equazione (3) deve essere soddisfatta consecutivamente n volte per evitare il rilevamento prematuro del segmento lineare. Il criterio è implementato in tempo reale per f S = 400 Hz e n = 8.
In seguito, Dotsinsky e Daskalov hanno definito il criterio come due differenze non successive:
Cr = |FDi+k- FD i | <M, per k >1 (4)
Questo approccio rende più precisa la transizione da segmento lineare a non lineare.
Compensazione delle variazioni di ampiezza del PL
Più frequentemente le correzioni sono aggiornate, migliore è la compensazione delle variazioni di ampiezza del PL. Pertanto, la soglia del criterio lineare, M, deve essere ragionevolmente meno restrittiva in modo che gli errori, commessi facendo la media di alcuni segmenti che si discostano dal segnale lineare ideale, siano più piccoli degli errori, che appariranno se M avvia l’aggiornamento sporadico della correzione. Inizialmente, M è stato fissato a 160 μV . Più tardi, valori euristici sono stati trovati essere M = 150 μV e M = 100 μV .
Filtraggio lineare
Per un numero dispari di campioni n = 2m + 1 in un periodo dell’interferenza PL, il valore filtrato:
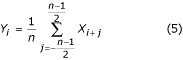
è fase-coincidente con quello non filtrato.
In caso di numero pari n = 2m, i due valori sono sfasati di metà del periodo del campione:
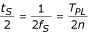
ma diventano coincidenti in fase usando la formula
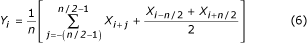
È possibile prendere per la media ogni secondo, terzo o qs campione se n/q è intero. A seconda che n/q sia dispari o pari, si usa rispettivamente l’equazione (7) o (8).

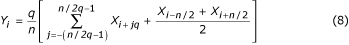
Un caso speciale di massima riduzione del campione si presenta con q = n/2 . La formula corrispondente:
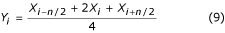
è chiamata filtro a tre punti. Oltre all’equazione (8), la seguente formula
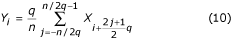
può anche essere applicata se q è pari. Nel caso di q = n/2, il filtro diventa ‘a due punti’ ed è rappresentato da:

La riduzione del numero di campioni in un periodo dell’interferenza porterà ad una maggiore pendenza dei lobi del filtro a pettine e ridurrà il tempo di calcolo. Tuttavia, questi “vantaggi” devono essere valutati attentamente per non violare la regola di Nyquist con una grande quantità di terza armonica presente. Le altre armoniche non sono prese in considerazione poiché le armoniche dispari più alte sono di solito soppresse da filtri passa-basso con cut-off nell’intervallo di 100-150 Hz, mentre quelle pari sono praticamente assenti a causa della precisa fabbricazione dei poli dei generatori delle centrali elettriche.
Compensazione della variazione di frequenza PL
La deviazione consentita dalla frequenza nominale PL è limitata in alcuni paesi fino all’1% dalle norme. In pratica, la deviazione è spesso più alta. Kumaravel et al. hanno riportato una variazione del 3%. McManus et al. hanno trovato notevoli variazioni nella frequenza di interferenza, che si sovrappone alle registrazioni prese dal database Common Standards for Electrocardiography (CSE).
Le variazioni di frequenza portano a un caso speciale di campionamento non multiplo con n reale, invece di uno intero. Questa complicazione può essere aggirata se le deviazioni sono rilevate dalla misurazione hardware continua di f PL e corrette da piccoli aggiustamenti dell’intervallo di campionamento t S intorno al suo valore nominale (R), t RS = T RPL /n (qui, T RPL = 20 ms è il T PL nominale per f RPL = 50 Hz). Per f PL , deviazione tra 49,5 e 50,1 Hz, le variazioni di t S sono nell’intervallo dell’1%, e di conseguenza non introducono errori oltre la precisione di misurazione accettata dei parametri che sono solitamente utilizzati per la classificazione automatica dell’ECG.
Un primo approccio associa l’innesco di ogni primo campione, S 1 , delle sequenze S k (k = 1, 2…n) nei periodi T PL con un’ampiezza arbitraria scelta ma costante della tensione PL. I campioni successivi, S k (k = 2…n), sono distanziati a t S , che si ottiene da t S = T RTL /n. Per 50 Hz e n = 5, t S = 4 ms. Due tipi di errori commessi con questo approccio sono studiati da Dotsinsky e Daskalov . Il primo, dovuto alle irregolarità inter-campione, può raggiungere 1% a f S = 400 Hz e 1,2% a f S = 250 Hz, in caso di deviazione 1% intorno alla f RPL . Il secondo tipo di errore non supera il 3% ed è una conseguenza della posizione ulteriormente spostata del campione filtrato.
Dotsinsky e Daskalov hanno riportato un approccio migliore. Il periodo in corso T PL viene misurato e diviso per n. Il t S ottenuto è usato nel successivo T PL.
Valutazione dell’efficienza della procedura
Esempi di procedura di sottrazione sono mostrati in Fig. 4 e Fig. 5. I segnali ECG sono presi dal database dell’American Heart Association. I segnali sono filtrati con notch per sopprimere l’interferenza di 60 Hz (frequenza PL negli Stati Uniti). Poi, i segnali sono mescolati con un’interferenza di 50 Hz, modulata in ampiezza da 0 a 3,2 mVp-p con uno slew rate di 200 μVs-1. Le tracce sono identificate come segue: i) segnale di ingresso; ii) interferenza sintetizzata; iii) segnale misto; iv) segnale elaborato; v) differenza tra segnali originali e elaborati e vi) differenza ingrandita. In realtà, i componenti scartati includono anche l’elettromiografia (EMG) e altri rumori. Una parte non soppressa del segnale, insieme a piccole interferenze residue e distorsioni dovute al compromesso con il valore M sono anche presenti nelle differenze.
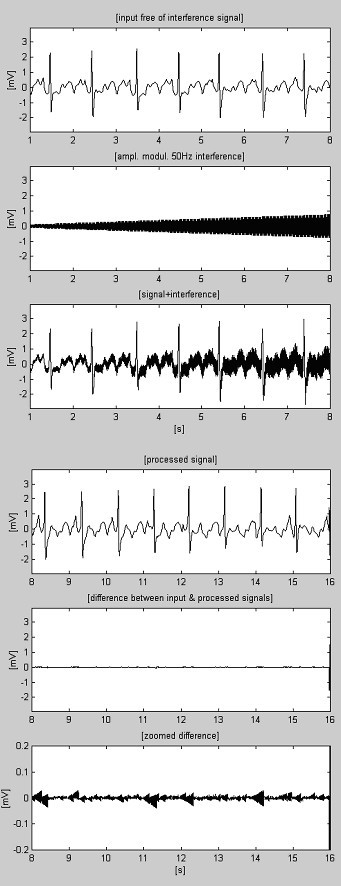
Registrazione elaborata AHA 3004d1.
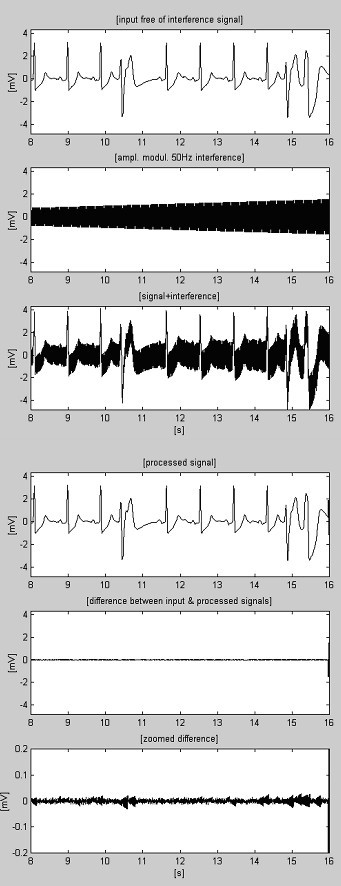
Registrazione AHA 6007d1 elaborata.
Due segnali sono utilizzati per valutare l’efficienza della procedura di sottrazione rispetto alla sola interferenza. Il primo, preso dal nostro stesso database, è chiamato condizionatamente ‘pulito’ (Fig. 6). Il risultato mostra piccole differenze tra i segnali in ingresso e quelli elaborati, visivamente dovute al rumore presente in ingresso. Questo risultato è verificato con il secondo segnale sintetizzato, che non contiene alcun disturbo (Fig. 7). Come si può vedere, non vengono introdotte distorsioni. Lo stesso segnale sintetizzato viene sovrapposto all’interferenza ed elaborato (Fig. 8). Non si trovano interferenze residue.
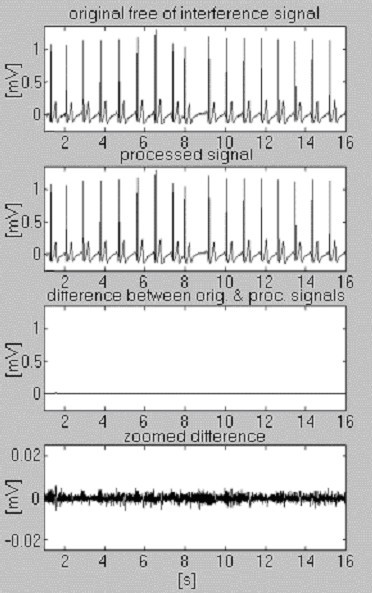
L’elaborazione del segnale condizionatamente ‘pulito’.
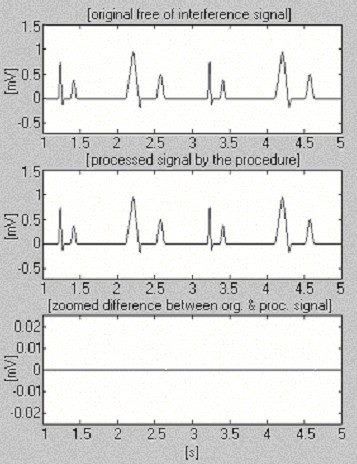
Processo del segnale sintetizzato.
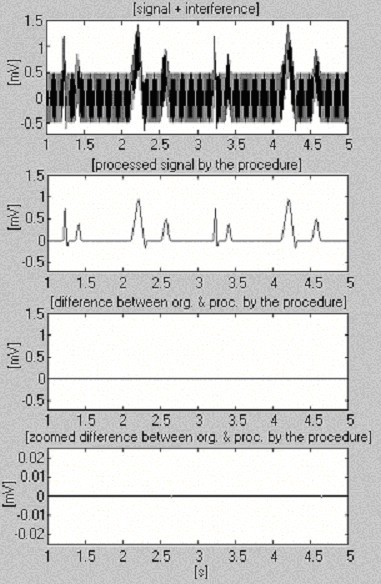
elaborazione segnale sintetizzato+interferenza.
Influenza del rumore EMG
A volte il rumore EMG è così alto che la ricerca del segmento lineare è ostacolata. Di conseguenza, correzioni imprecise, che non corrispondono all’ultimo cambiamento dell’ampiezza dell’interferenza, causeranno errori (vedi il rumore residuo tra l’11° e il 14° s in Fig. 9).
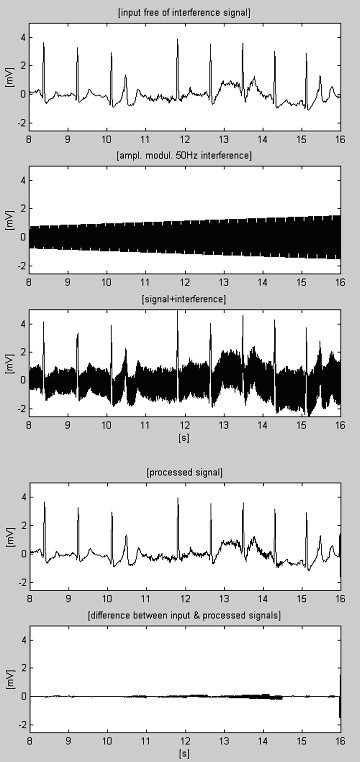
Segnale ECG elaborato+rumore EMG+interferenza.
Un approccio molto semplice per la soppressione dell’influenza del rumore EMG sulla procedura introduce un buffer parallelo addizionale dove le porzioni in corso del segnale sono mediate incondizionatamente. Questo buffer viene utilizzato per un accurato rilevamento della linearità. La Fig. 10 e la Fig. 11 mostrano il confronto dei risultati senza e con il buffer parallelo. Le tracce ‘a’ rappresentano il segnale ECG mescolato con interferenze e rumore EMG. Le tracce ‘b’ in Fig. 10 e ‘c’ in Fig. 11 indicano le transizioni da segmenti lineari a non lineari (funzioni on-off). Come si può vedere, la parte di segnale medio in Fig. 10 è molto limitata. Di conseguenza, l’efficienza della procedura è ridotta (Fig. 10c e 10d. Al contrario, il buffer parallelo permette il rilevamento di lunghi segmenti lineari (Fig. 11c e il rumore residuo nel segnale elaborato (Fig. 11d è basso. Tuttavia, il rumore non è totalmente soppresso perché una parte di esso partecipa al calcolo di correzione.
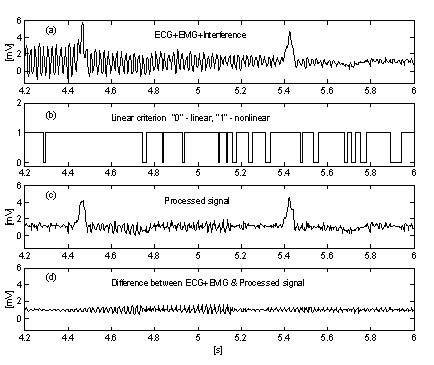
Sottrazione di interferenza+rumore EMG senza buffer parallelo.
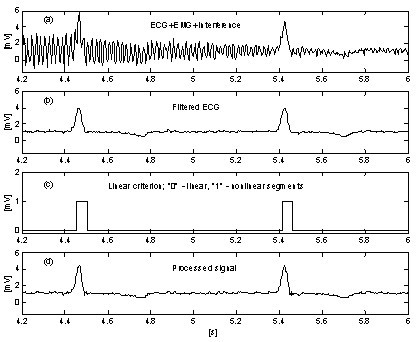
Sottrazione di interferenza+rumore EMG con buffer parallelo.
Un ulteriore miglioramento nella soppressione del rumore EMG è ottenuto da Christov utilizzando il valore di soglia adattativo M, che è calcolato rispetto al rapporto rumore/segnale Rt, definito come Rt = S NL /S F , dove il livello di rumore S NL è uguale alla larghezza sommaria dei segmenti non lineari in un’epoca S F , corrispondente approssimativamente all’intervallo RR in esame. La ricerca di linearità con un criterio di M = 150 μV per ECG ‘pulito’ (Fig. 12a) e per lo stesso segnale, ma contaminato da rumore EMG (Fig. 12b) mostrano diversi S NL , (Fig. 12c e 12d). Il metodo è sviluppato in ambiente MATLAB. La soglia iniziale M è scelta pari a 30 μV. Poi, viene gradualmente aumentata fino a quando Rt raggiunge il 10%, dopo di che viene avviata la procedura di sottrazione. Il valore Rt ≤ 0,1 è suggerito dal rapporto “larghezza QRS contro il suo intervallo RR”, che di solito è intorno al 10%. L’eliminazione di entrambe le interferenze e il rumore EMG può essere osservato in Fig. 13b e 13d, dove M = 420 μV è usato. Per confronto, il segnale ECG ‘pulito’ viene elaborato con M = 35 μV (Fig. 13a e 13c).

Livelli di rumore SNL (tracce c e d) in segnale ECG ‘pulito’ (traccia a) e segnale contaminato EMG (traccia b), rispettivamente.
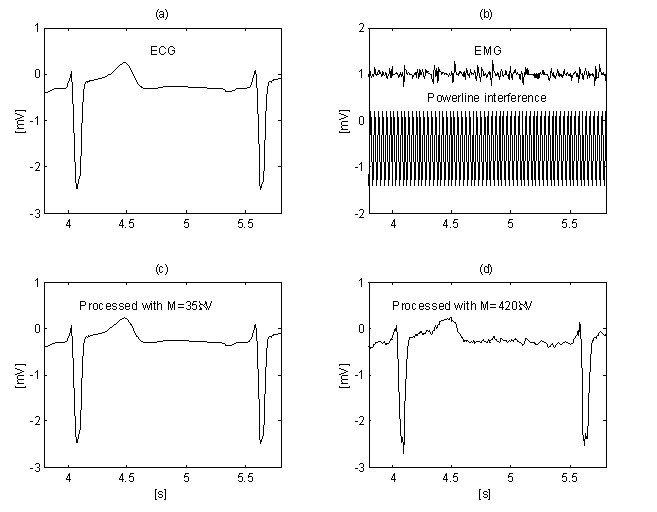
Soppressione del rumore EMG+interferenza usando la soglia adattiva M: ‘segnale pulito’ (a) elaborato con M = 35 μV (c) e segnale contaminato (b) sottoposto alla procedura con M = 420 μV (d).
I segmenti lineari non possono essere trovati regolarmente nei pazienti con fibrillazione atriale e ventricolare. Tuttavia, la conservazione totale della forma d’onda non è necessaria per il rilevamento della fibrillazione e quindi, tutti i tipi di filtri tradizionali possono essere applicati.
Soppressione delle interferenze nell’ECG ad alta risoluzione
La procedura di sottrazione non è direttamente applicabile all’ECG di His sulla superficie del corpo, poiché l’onda di His a bassa ampiezza e relativamente bassa frequenza non può essere distinta in segmenti lineari. Pertanto, l’onda di His sarà, in pratica, soppressa o addirittura rimossa dal segnale. Il rumore EMG è di solito di maggiore ampiezza e con un contenuto di frequenza molto più alto rispetto all’onda di His superficiale. Pertanto, il semplice cambiamento del valore di soglia, M, non risulta in una delineazione accettabile dei segmenti lineari e non lineari.
Bazhina et al. hanno implementato la seguente modifica. L’inizio del segmento non lineare rilevato prima di un complesso QRS è spostato di 100 ms a sinistra, definendo così la regione dell’onda di His come un segmento non lineare per difetto (Fig. 14).
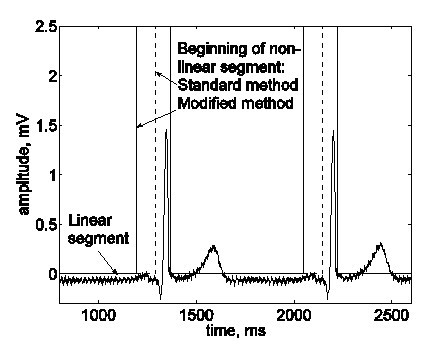
L’inizio di un segmento non lineare che include il complesso QRS è stato spostato di default di 100 ms a sinistra, per includere la zona dove ci si aspetta che appaia l’onda di His.
La procedura di sottrazione e altri tre metodi: filtri notch, interpolazione spettrale e sottrazione di regressione sono stati testati contro la distorsione minima del segnale originale. Le procedure di sottrazione e di regressione-sottrazione si sono rivelate le migliori, poiché Baratta et al. usano un concetto simile per la stima del rumore nei segmenti lineari. La sottrazione di regressione si occupa male dei cambiamenti di ampiezza dell’interferenza all’interno del segmento corrente.
Caso di dispositivi alimentati a batteria e sistemi ECG computerizzati
La misura hardware di f PL , necessaria per la compensazione della modulazione di frequenza dell’interferenza, non è fattibile nei dispositivi alimentati a batteria e in alcuni sistemi ECG computerizzati. Dotsinsky e Stoyanov hanno studiato la gamma di variazioni di frequenza dell’interferenza con ampiezza costante, per la quale la parte residua è limitata a livelli accettabili senza uso di campionamento sincronizzato. Hanno trovato che l’interferenza residua sotto 20 μVp-p potrebbe essere ottenuta con la procedura da: i) ampiezza di interferenza ≤ 0.4 mVp-p e ii) cambiamento di frequenza con un tasso ≤ 0.0125 Hzs-1. Poiché tali requisiti per l’alimentazione possono spesso essere superati, è stato sviluppato un software di misurazione delle interferenze.
Il segnale ECG viene inizialmente elaborato da un filtro passa-banda da 49-51 Hz. Vengono misurate le ampiezze di due campioni adiacenti, Br L e Br R , presi da una pendenza positiva dell’interferenza, situati sotto e sopra la linea dello zero (Fig. 15). La distanza, t CP , tra il punto di incrocio CP e il campione di destra, Br R , è calcolata continuamente da:
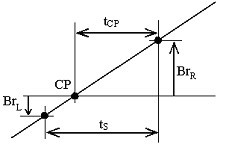
Interferenza zero crossing.

In caso di cambiamento di T PL, t S è ridefinito usando

Questo approccio è stato implementato in ambiente MATLAB. Per la frequenza di campionamento f S = 500 Hz e f RPL = 50 Hz, n è uguale a 10. Il prodotto kn determina il tempo raccomandato per trascorrere prima di calcolare e sostituire il nuovo tCP,i + kn per il precedente tCP,i. La Fig. 16 mostra un segnale ECG elaborato da 1 mV dopo essere stato mescolato da un’interferenza con 2 mVp-p di ampiezza costante ed estremamente veloce che varia di 1 Hz per 8 s di frequenza (prima traccia). Per valutare l’efficienza ottenuta, viene presentata anche la differenza ingrandita senza campionamento sincronizzato (ultima traccia).
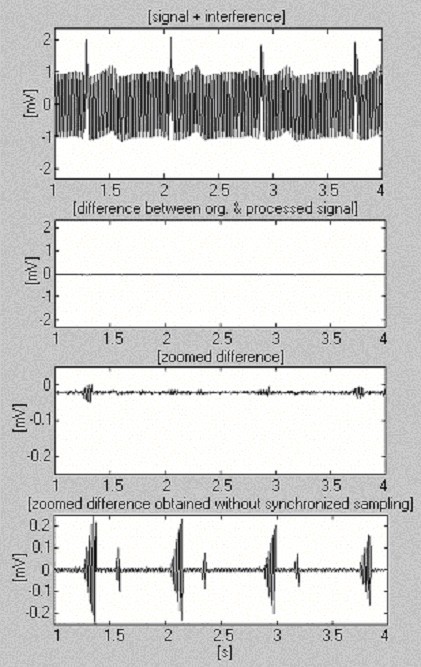
Procedura di sottrazione utilizzando la misura della frequenza della linea elettrica del software.
Il prossimo passo logico da fare consiste nel: i) mantenere la t S nominale dello strumento ECG, ii) ricampionare il segnale secondo la f PL misurata in corso per eliminare l’interferenza e iii) tornare alla t S nominale. I primi risultati di tale approccio sono molto promettenti. Così, la compensazione software della variabile f PL , così come una totale implementazione della procedura di sottrazione in uno strumento, compresa la regolazione automatica per f RPL di 50 o 60 Hz, sarà completata indipendentemente dai circuiti hardware e il software corrispondente.
Adattamento automatico alla frequenza nominale PL
Un programma comune per la sottrazione di interferenze alternative in ambiente di 50 e 60 Hz porta a un campionamento non multiplo, cioè a n reale. Valori ampiamente usati di t S per f RPL = 50 Hz, come 250, 500 e 1000 Hz, corrispondono a n irrazionali di 4.1(6), 8.3(3) e 4.1(6) se si devono eliminare interferenze di 60 Hz. Nel caso inverso, f S = 360 Hz richiede n = 7,2. I valori arrotondati n* sono inaccettabili da usare, poiché introdurrebbero un errore considerevole.
Una soluzione molto semplice che non ha bisogno di cambiare f S è stata trovata da Dotsinsky e Stoyanov . La procedura originale applica un filtro a pettine su un periodo, T PL , dell’interferenza. Così, il programma viene eseguito più velocemente. In generale, n può essere preso da k > 1 periodi interi. La procedura funziona se:
n = kT PL /t S è un intero.
Per t S = 2 ms (f S = 500 Hz) e f RPL = 50 Hz, il più piccolo valore di k che soddisfa l’equazione (14) è proprio k = 1. Tuttavia, nel caso di 60 Hz, k è uguale a 3. Gli zeri associati alle subarmoniche 20 e 40 Hz appariranno anche ma non hanno alcuna influenza sulla procedura. Pertanto, è sufficiente commutare n tra 10 (k = 1) e 25 (k = 3) per operare con entrambe le interferenze. A questo scopo due filtri digitali passa-banda controllano il segnale in entrata. La Fig. 17 mostra che il filtro con banda di frequenza che si sovrappone all’interferenza genera un segnale in uscita di un ordine di grandezza superiore all’altro filtro.
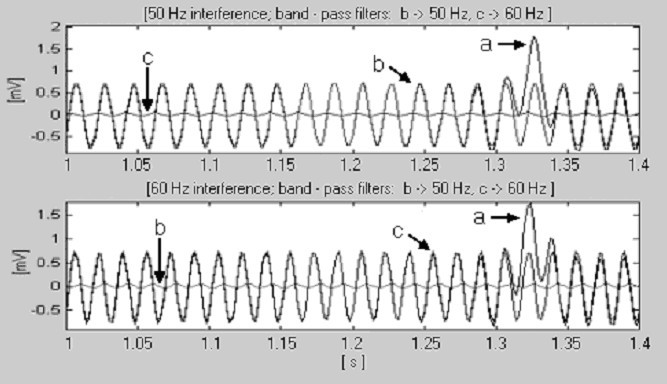
Rilevamento della frequenza nominale della linea elettrica, a) parte del complesso QRS, b) interferenza a 50 Hz e c) interferenza a 60 Hz.
Sviluppo della procedura teorica
La teoria della procedura di sottrazione è stata sviluppata ulteriormente da Mihov , Levkov e Mihov , e Mihov et al. Hanno proposto quattro tipi di filtri, implementati in una struttura generalizzata che può superare i problemi con quasi tutti i casi di campionamento non multiplo, comprese le variazioni di frequenza di interferenza, senza utilizzare la conversione AD sincronizzata.
Il cosiddetto filtro D nel campionamento multiplo è definito come è Cr nell’equazione (2), dove la seconda differenza, D i , si ottiene con FD s che sono distanziati a un T PL :
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
La funzione di trasferimento del filtro D ha degli zeri a f = 0 e f = f PL Hz, che è mostrato uguale a 50 Hz in Fig. 18.

Funzione di trasferimento del filtro D per fPL = 50 Hz.
Il filtro K descrive la media mobile presentata dalle equazioni (5) e (6). La sua funzione di trasferimento è data in Fig. 19 per n = 5 in caso di molteplicità dispari.
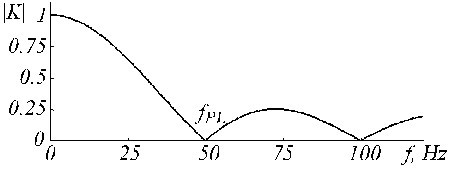
Funzione di trasferimento del K-filtro per fPL = 50 Hz e n = 5.
L’equazione usata per il calcolo continuo delle componenti di interferenza:
B i = X i – Y i (16)
definisce effettivamente un filtro digitale chiamato (1-K)-filtro.
Inoltre, i filtri sono ridefiniti per il campionamento non multiplo, e f S = 250 Hz in combinazione con f RPL = 60 Hz è preso in considerazione per illustrare il miglioramento del software.
Per preservare gli zeri della funzione di trasferimento, il filtro D deve essere sottratto con un filtro di correzione con zero a f = 0 e guadagno di D RPL a f = f RPL , uguale al guadagno del filtro D per la stessa frequenza, f RPL . La sintesi del filtro di correzione si basa su un filtro ausiliario a tre punti dato dall’equazione:

dove (n/2)* è il valore arrotondato di n/2.
Siccome A RPL è il guadagno del filtro ausiliario per f = f RPL , il filtro di correzione viene moltiplicato per il rapporto D RPL /A RPL . Usando le funzioni di trasferimento corrispondenti, D RPL e A RPL sono calcolati in anticipo da:
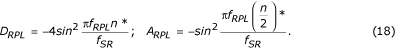
Finalmente, il filtro D* corretto è presentato come

e viene mostrato in Fig. 20 dalla traccia ‘c’, dove le tracce ‘a’ e ‘b’ sono rispettivamente il filtro D e il filtro di correzione.
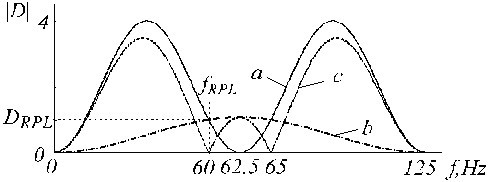
Funzioni di trasferimento di a) filtro D, b) filtro di correzione ausiliario e c) filtro D corretto.
La funzione di trasferimento del filtro K deve conservare zero per f = f RPL, guadagno unitario per f = 0 e risposta di fase lineare. La procedura di correzione del filtro K è simile alla precedente. Un filtro ausiliario è dato dalla formula usata per il calcolo delle correzioni:
A i = X i – Y i , (20)
Il guadagno del filtro è uguale a 1 – K RPL per f = f RPL , dove K RPL è il guadagno del filtro K per la stessa frequenza f RPL . Il filtro ausiliario è moltiplicato per K RPL /(1 – K RPL ) e sottratto dal filtro K. L’equazione per il filtro K* corretto è:
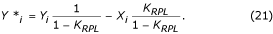
La costante K RPL può essere stimata da:

per molteplicità dispari o pari, rispettivamente.
Un esempio di correzione del filtro K è mostrato in Fig. 21, dove le tracce ‘a’, ‘b’ e ‘c’ rappresentano il filtro K primario, il filtro ausiliario e il filtro K* corretto.
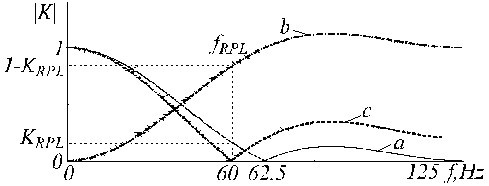
Funzione di trasferimento di a) filtro K, b) filtro ausiliario di correzione e c) filtro K corretto.
In caso di campionamento non multiplo, appare una differenza di fase tra i campioni ECG in corso e le componenti di interferenza B i (equazione 16) solitamente situate in un buffer temporaneo first-in-first-out (FIFO). Pertanto, B i deve essere modificato e sottratto dai campioni ECG durante i segmenti non lineari. La procedura di compensazione è relativamente complicata. La Fig. 22 mostra il contenuto del buffer temporaneo. L’attuale campione di interferenza, B i-n *, non coincide con il campione restaurato, B i . La sua ampiezza deve essere ricalcolata per compensare la differenza di fase tra loro. Questo è realizzato da un nuovo filtro con risposta di fase lineare e guadagno unitario per f = f RPL, indicato come il filtro B. Esso è sintetizzato dal noto filtro K, con una finestra pari al periodo di interferenza. In caso di n* dispari, può essere descritto come:
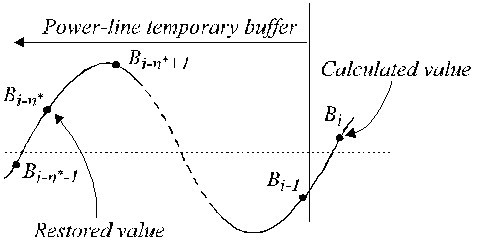
Valori ripristinati nel buffer temporaneo.
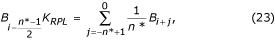
dove K RPL è il guadagno per l’interferenza del filtro di media dato dall’equazione (22).
Il valore di buffer ripristinato B i può essere calcolato da:
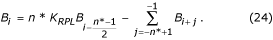
In caso di n* pari:
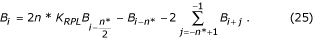
La funzione di trasferimento del filtro B è mostrata in Fig. 23.
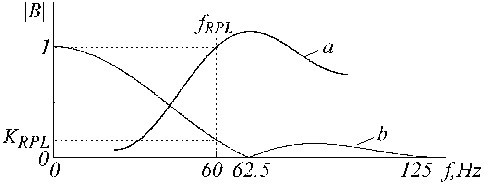
Funzioni di trasferimento di a) filtro B e b) il noto filtro K.
La struttura generalizzata è presentata in Fig. 24, dove i moduli della procedura di sottrazione sono i seguenti:
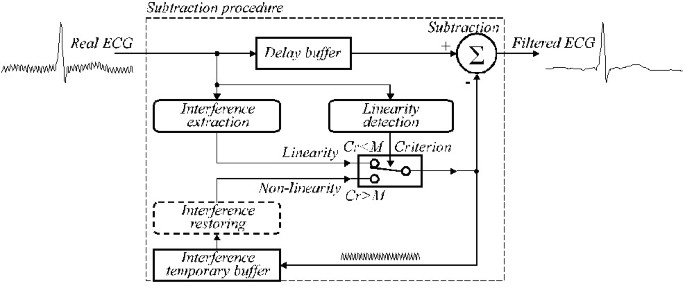
Struttura generalizzata della procedura di sottrazione.
-
Rilevamento della linearità. Il filtro D viene applicato per valutare la linearità di ogni vicinato del campione del segnale.
-
Estrazione delle interferenze. (1-K)-filtro è usato per calcolare la componente di interferenza.
-
Criterio. La condizione Cr <M invia l’interferenza PL estratta o restaurata a Sottrazione.
-
Buffer temporaneo di interferenza. La componente di interferenza estratta o restaurata usata come correzione nel segmento non lineare è salvata nella posizione bloccata con la fase in corso dell’interferenza della linea elettrica.
-
Interferenza di ripristino. Il filtro B viene chiamato in caso di campionamento non multiplo per ripristinare i veri valori di correzione, che devono essere sottratti dai campioni del segnale di ingresso nei segmenti non lineari.
-
Buffer di ritardo. Compensa il ritardo che appare con il filtro D e il filtro (1-K) ed è imperativo se la procedura viene eseguita in tempo quasi reale. Altrimenti, il buffer potrebbe essere ignorato.
-
Sottrazione. Il valore di interferenza estratto o ripristinato viene sottratto dal segnale di ingresso ritardato per produrre un segnale ECG “pulito”. In caso di non linearità, sia l’estrazione delle interferenze che la sottrazione implementano il filtro K.
Un algoritmo migliorato secondo la struttura generalizzata è stato testato off-line. I risultati per f S = 250 Hz e f RPL = 60 Hz sono mostrati in Fig. 25.
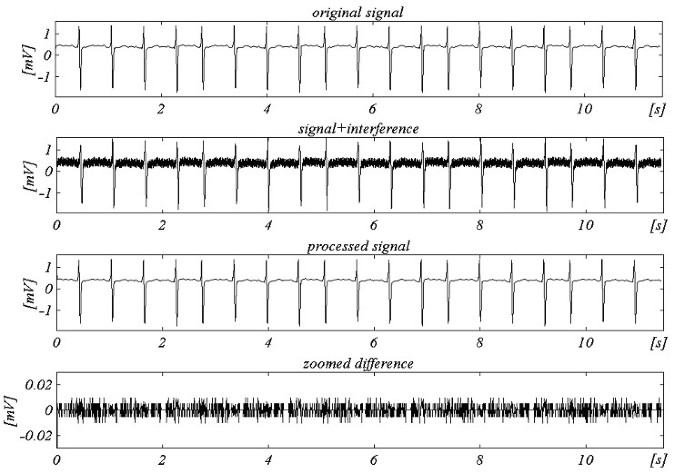
Esempio per campionamento non multiplo con fRPL = 60 Hz e fS = 250 Hz.