絶対速度の解析

Abstract
Key words
時間の相対性
長さの相対性

Abstract

光は光源の動きや観測者の参照枠に関係なく、真空中を速度cで進む。そのため、光源から観測者までの空間的な移動に時間がかかり、発光と観測が同時に行われない。このような考察から、閉じた船室の中から宇宙船の運動状態を把握するために、観測者の絶対速度を測定する方法を提案する。

Key words

座標系、参照系、運動、絶対速度、相対論、ローレンツ変換、時間、空間、観測者、光源
以下の解析は、密閉された船室から宇宙船の運動状態を決定するために使用できる観測者の絶対速度の測定方法を実用化するためのものである。絶対速度とは、一般に、ある物理系を構成する様々な物体が、その中に含まれる物理物体から独立して存在する不動の空間（＝絶対空間）に対して、標準的な一様速度を持つことを指す概念である。ここでは、剛体運動論に基づくアプローチにより、光源や観測者の参照枠の運動に関係なく、光が真空中を速度cで進むことから、観測者の絶対速度が決定されることを示す。したがって、光源から観測者までの空間的な移動には時間がかかり、発光と観測が同時に行われることはない。点(0,0,0)を原点とする3本の直交軸からなる直交座標系を仮定し、空間上の任意の点Pは実数の順序付き組(x,y,z)で表されるx、y、z軸上の座標によって定義できるものとする。慣性基準系Sは、原点をOとする空間直交座標系（x,y,z）で表されるとする。S内の静止点には、一連の標準時計（S時計とする）が配置され、S時計は光信号の送受信により相互に校正（同じ瞬間に同等の測定値を提供）されている。具体的には、時刻tAに時計Aから時計Bに向けて光線を投射し、時刻tBに時計Bで時計Aに向けて反射し、時刻tA’に時計Aに到達する。の場合、2つの時計は較正されている。座標x,y,zに位置する任意のイベントに対して、その時間座標tはイベントに関連するSクロックの読みによって与えられる。同様に、原点をO’とする第2の空間直交座標系（x’，y’，z’）に基づいて別の慣性基準系S’が確立され、別の一連の相互に校正された標準時計（S’時計）は基準系S’の静止点に配置されている。座標x’,y’,z’に位置する任意のイベントに対して、その時間座標t’はイベントに関連するS’クロックの読みによって与えられる。
空間座標と時間座標のそれぞれの起源、および座標軸の方向はかなりの程度任意に選択できるので、ここで採用するSとS’の関係は以下の規則に基づいており、簡単のため適用したものである。
(1) ある瞬間に、2つの系の原点と座標軸を重ね合わせ、OとO’にそれぞれ位置する時計をゼロにする、すなわち。
(2) SとS’の相対運動方向においてx軸とx’軸は一致している。したがって、xとx’は常に一致し、yとy’、およびzとz’は平行になる。
(3) Sの+x方向にS’が移動する。
この提案する解析は、真空中の光が観察者と光源のどちらの運動によっても一定速度cで移動するという基本原理に基づいている。したがって、ここでは、直線的で一様と仮定した観測者の絶対速度Uをと定義し、f（φ）は光信号の方向とUの方向との幾何学的関係の関数を表し、ここではφと表す。
時間および長の相対性については、アインシュタインの説明（「移動体の電気力学について」を参照）とは異なる、二つの新しい説明を提案する分析が提供される。

時間の相対性

光の速度が有限である以上、光が光源から空間の観測者に到達するまでにある程度の時間が必要であり、その時間は光源から観測者までの距離と同じである。したがって、光の発射と観測が同時に行われることはない。光の速度が一定であることと、図1に示した条件をもとに、次のような要素を定義する。光源が発光した時（事象Rとする）、における光源と観測者の位置をそれぞれA、H0とする。 4255＞から＜3294＞までの光の伝播の間に、観測者は位置H0からHまで距離U・Tを移動し、そこで観測者は発光した光を受ける。したがって、を、で光信号を受信したときの観察者の位置と、で発光したときの光源の位置との間の距離lと定義する。光の速度が一定であるため、となる。距離はU・Tに相当する。最後に、の観測者の位置との光源の位置との間の距離l0をと定義する。ここで、従来は物理的な意味を持たないと考えられていた点の観測者の位置についての考察を紹介する。観測者と光源の運動状態が等価であれば、l0が与えられ、図1に示す三角関係でUが計算できる。観測者と時計は共に原点に置かれる。事象の発生を表す光信号が観測者に到達したとき、光の到達時刻は時計の示す時刻と一致する。この対応関係の利点は、時計を使う観測者の位置と常に関連していることである。図1に見られるように、空間点O3は、＜6382＞で発光するときの光源の位置に基づいて定義することができ、空間点O2は、＜8678＞で光を受けるときの観測者の位置に基づいて定義することができる。しかし、光源が＜1733＞で発光したときに観察者が位置する空間点O1を定義する手段は自明ではない。この問題を解決するために、絶対静止（＝）と絶対運動（＝）の概念を導入する。それぞれ、H0とHにいる1人の動く観測者を、空間点O1とO2に静止している2人の観測者H1とH2に置き換え、光源Aは空間点O3に静止しているとする。観測者と光源はそれぞれ較正された標準時計を使用しており、Aはで光信号を発し、イベントR0と表記する。観測者H1がcで進む光信号を受信したときの時計の読みはT0であり、H2が受信したときの読みはTである。このように、距離とは光信号のそれぞれの移動時間に基づいて次のように定義できる：
, (1)
and
. (2)
図1に示す三角関係により、観測者H1、H2間の事象R0の変換は次のように与えられる。
(3)
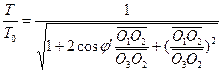(4)
ここで、は直線O3O1とx軸との間の角度であり、は直線O3O2とx軸との間の角度である。
ここで、移動する観測者が1人の場合に話を戻すと、システムSにおいて、観測者Hと光源Aはともに較正された標準時計を使用しているとする。事象Rの瞬間、光源Aは空間点O3にあり、観測者HはO1にいる。光信号が空間点O1に到達する瞬間は、Sクロックの読みがT0に相当する。観測者Hが光信号を受け取った時の読みはTで、HはO2にいる。
もちろん、Hは点O1での事象Rを観測できない。この問題を解決するために、別の観測者H-をシステムS内のに対応する点O1に配置し、H-の位置を空間点O1の定義に採用する。そして、観測者H-とHの間の事象Rの変換は、式（3）により、以下のように求めることができる。
(5)
したがって、式（3）及び式（4）は以下のように書き換えることができる。
(6)
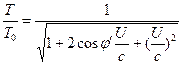(7)
e また、について、式（6）及び（7）が以下に単純化することを観察することができる。
(8)
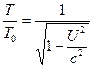(9)
したがって、以上の解析から、（φ）が分かっていれば、式（6）からUを求める簡単な方法を得ることができる。
簡単のために、参照枠として観測者と等価な運動状態を持つ光源を選ぶ。一様に直線運動する剛体の棒の中心に観測者を置き、棒上の異なる位置からの光信号が異なる時刻に観測者に到達する。オブザーバはオブザーバの位置で式（8）から得られる偏向角を持ったバーの偏向を検出する。
この方法によって、宇宙船の運動状態を閉じた機内から求めることができた

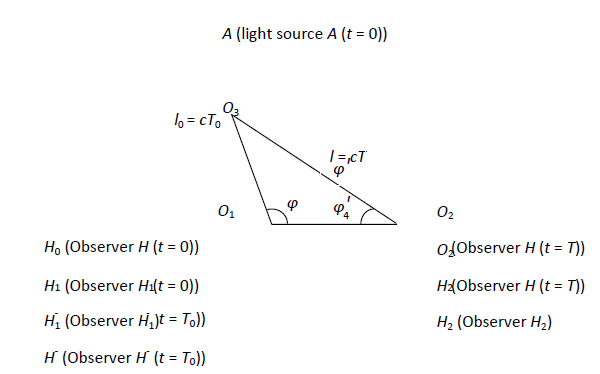
図1：観測者と光源の運動状態

長さの相対性

上記の解析では、とという二つの長さが導入されている。この場合、その座標系内では長さLの静止剛体棒と仮定し、そのLを静止スタッフゲージで測定し、棒軸を＋x方向に絶対速度Uで一様直線運動する座標系のx軸に一致させ、Lは以下に定義する二つの操作で決まると仮定する。
(a) 観察者は棒およびスタッフ・ゲージと同じ移動座標系に存在し、棒とスタッフ・ゲージを重ね合わせてLを測定する。
(b) 静止座標に置かれた複数の時計が同期して動くことにより、観察者は特定の瞬間tに棒の両端の位置を静止座標で測定し、その間の距離を静止スタッフ・ゲージで測定する。は操作（a）から算出された長さで、本明細書では移動座標におけるバー長さと表記する。は操作(b)から計算された長さであり、本明細書では静止座標における移動バーの長さとして表記している。 4898＞と＜6637＞が異なることは明らかである。＜3963＞ここで、システムSにおいて、観察者H-がHと同じ運動状態にあると仮定すると、図1に示すように、＜9869＞で光信号を受信したとき、H-は点O1におり、同時に、観察者Hは点O4にいるとする。したがって、t=0.04
はにおけるH-とHとの距離であり、
となる。 (10)
はT0からTまでの区間で観測者Hが移動した距離で、
のようになる。 (11)
は地点のH-と地点のHの距離で、
のような値である。 (12)
このように、次の式が導かれる。
(13)
次に、ローレンツ変換の新しい説明として、線速度が均一な2つの移動座標系間の座標変換と時間変換について考えてみることにする。
観察者H（システムS内）、観察者H’（システムS’内）、光源A”（システムS”内）が、それぞれ校正された標準時計を用い、で、光源A”から光信号（イベントR”と表記）が放射されたと仮定します。イベントR”の瞬間、A”は点O3にあり、観測者HとH’は一致する。観測者Hが光信号を受信したとき、Sクロックの読みはTであり、Hは点O1にいる。観測者H’が光信号を受け取ったとき、S’のクロックの読みはT’で、H’は点O2にいる。すると、観測者H’とHの間の事象R”の変換は式（3）より計算でき、ここで
となる。 (14)
ここで、uは観測者H’とHの間の相対速度であり、以下の変換が得られる。
(15)
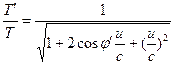(16)
より、次の関係が得られる。
. (17)
とのとき、(16)式は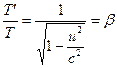
と簡略化される。 (18)
したがって、以下の変換関係が推論される：
、(19)
、(20)
、(21)
。 (22)
、(23)
、(24)
、(25)
、(26)
のとき、さらに。 (27)