許容範囲
このセクションでは、片側および両側の許容範囲に関する統計的な詳細について説明します。
正規分布に基づく区間
片側区間
片側区間は次のように計算されます。
Lower Limit =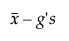 
Upper Limit =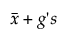 
ここで
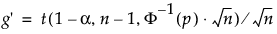
sは標準偏差
tは非標準曲線からの分位値であり、この分位値を用いて、
と
を計算する。中心t分布
Φ-1 は標準正規分位
Two-Sided Interval
両側間隔は次のように計算される。
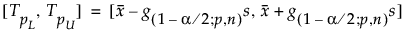
ここでsは標準偏差、g(1-α/2; p,n) は定数とする。
gを決定するためには、許容区間によって捕捉される母集団の割合を考える。 Tamhane and Dunlop (2000)はこの割合を次のように与えている：
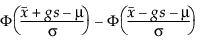
ここでΦは標準正規cdf（累積分布関数）である。
したがって、gは次の方程式を解く：
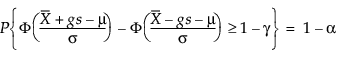
ここで1 – γは許容区間に含まれるすべての将来のオブザベーションの割合である.
正規分布ベースの許容区間の詳細については、表 J.1a, J.1b, J.6a, and J.6b of Meeker et al. (2017).
ノンパラメトリック区間
片側下限
サイズnのサンプルからのサンプリング分布の少なくとも割合βを含む下100（1-α）％片側許容限界は、順序統計量x（l）である。 指数lは次のように計算されます：
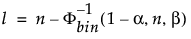
ここでΦ-1bin(1-α, n, β)はn回の試行と成功確率βを持つ二項分布の(1-α)番目の分位値であり、(1-α)番目の分位値は、(1-α)番目の分位値です。
実際の信頼度はΦbin(n-l, n, β)として計算され、Φbin(x, n, β)は試行回数n回、成功確率βがx以下の二項分布型確率である。
なお、下側の片側分布のない許容区間を計算するには、標本サイズnは少なくとも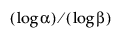
と同じ大きさでなければならない。
片側上限値
サイズnのサンプルからサンプリングした分布の割合βを少なくとも含む上限100（1-α）％片側許容限界は順序統計値x（u）である。 指数uは次のように計算されます：
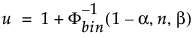
ここでΦ-1bin(1-α，n，β)はn回の試行を行い成功確率βの二項分布の（1-α）番目の分位数である。
実際の信頼度はΦbin(u-1, n, β)として計算され、ここでΦbin(x, n, β)はn回の試行と成功確率βがx以下の二項分布の確率である。
上片分布なしの許容範囲を計算するにはサンプルサイズnは少なくとも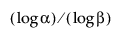
と同じくらい大きくなければならないことに注意すること。
両側許容区間
サイズnの標本からサンプリングした分布の少なくとも割合βを含むための100（1-α）％両側許容区間は次のように計算されます。
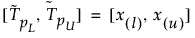
ここで x(i) はi次統計量、lとuは次のように計算される：
Let ν = n – Φ-1bin(1-α, n, β), ここで Φ-1bin(1-α, n, β) はn回の試行を行い成功確率βの二項分布の（1-α）番目の分位値である。 νが2より小さい場合, 両側分布のない許容区間は計算されない. νが2以上の場合、l = floor(ν/2) および u = floor(n + 1 – ν/2).
実際の信頼度は、Φbin(u-l-1, n, β) として計算され、Φbin (x, n, β) はn試行で成功βがx以下の確率を持つ2元分布のランダム変数であるとします。
両側分布のない許容区間を計算するためには、サンプルサイズnは少なくとも以下の式のnと同じ大きさでなければならないことに注意：
分布のない許容区間の詳細についてはMeekerら（2017、5.3項）参照
。