2次元およびその他のNMR実験に当社のNMRサービスをご利用ください。
2次元NMRの種類
2次元NMR分光法には以下があります:-
Homonuclear
- 結合を通して行う。 COSY, TOCSY, 2D-INADEQUATE, 2D-ADEQUATE
- Through space: NOESY, ROESY
Heteronuclear correlation
- One-bond correlation HSQC, HMQC
- Long-range correlation HMBC
2次元スペクトル割り当て例
12,14-ditbutylbenzochrysen

酢酸コレステリル

2次元NMRの基礎
1次元NMR実験では、パルスシーケンスの直後にデータ取得ステージが行われる。 この順序は、データ取得の前に準備段階が加わるものの、複雑な実験でも維持される。 しかし、2次元NMR実験では、データ取得の段階と励起の段階は、進化と混合という中間段階によって分離される。 進化は t1 と呼ばれる時間だけ継続する。 データ取得では、次のように多数のスペクトルが取得される。1回目はt1の値をゼロに近づけて最初のスペクトルを取得する。 2回目は、t1をΔtだけ増加させ、別のスペクトルを取得する。 このプロセス (t1 の増加とスペクトルの取得) を、2 次元フーリエ変換を使用して解析するのに十分なデータが得られるまで繰り返す。 スペクトルは通常、t1次元のスペクトルをf1軸、進化と混合の後に取得したスペクトルを2軸とする地形図として表現される(1次元取得と同様)。 信号の強度は、それが強いほど強い色で示されます。
結果として得られる地形図では、信号は2つの周波数(f1およびf2)の関数となります。 ある信号がある周波数(例えば20Hz)f1で現れ、別の周波数(例えば80Hz)f2で現れる可能性があり、それは信号の周波数が進化の時間の間に変化したことを意味する。 2D-NMR実験では、磁化の移動が測定される。 COSY、TOCSY、INADEQUATEのように同じ種類の原子核への結合で起こることもあれば、HSQC、HMBCのように別の種類の原子核への結合で起こることもあり、NOESY、ROESYのように空間を介して起こることもある。
さまざまな2次元NMR技術は、共鳴周波数が非常に似ているので信号が重なる場合など1次元NMRでは足りない場合に有効である。
基本的な2次元NMR実験(図1)は、2つのパルスまたはパルス群によって原子核を励起し、自由誘導減衰(fid)を受け取るパルスシーケンスで構成されています。 パルス群は純粋な高周波(rf)であっても、磁気勾配パルスを含んでいてもよい。 2つのパルス群の間の遅延(発展時間-t1)を増加させながら、取得は何度も実行される。 進化時間にはt1、獲得時間にはt2と表示される。 2Dパルスシーケンス
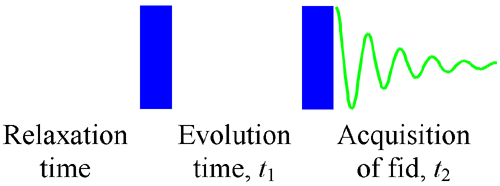
2Dフーリエ変換
次にFIDを両方向にフーリエ変換し(図2)、スペクトルを得ることができます。 このスペクトルは、従来はコンター図として表示されていた。 図2.2次元フーリエ変換
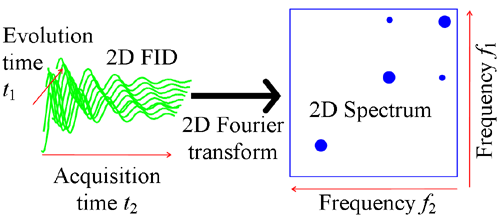
2次元スペクトルは、わかりやすいように1次元に投影してプロットされるのが普通です。 これらは本物の投影であってもよいし、同等の1次元スペクトルであってもよい。 2D-INADEQUATEを除く)これはピークとそれ自身の相関を表すもので、それ自体はあまり有益なものではありません。 対角線から離れた信号は2つの信号の相関を表し、割り当てに使用される。 例えば図3の同核COSYスペクトルでは、1.4ppmの1Hシグナルは2.8ppmの1Hシグナルとクロスピークがあるため相関があるが、7.8ppmのシグナルとは相関がない。図3 エチルベンゼンの2次元COSYスペクトル
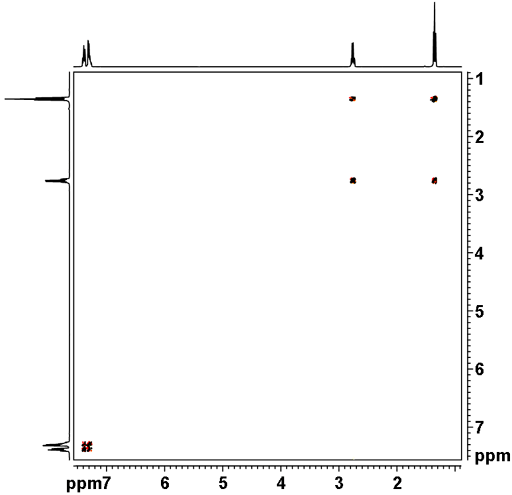
異核スペクトルでは対角のシグナルはなく、すべてのシグナルは相関を表しています。 例えば、図4の異核HSQC短距離相関スペクトルでは、1.4ppmの1Hシグナルは15.7ppmの13Cシグナルと相関し、2.4ppmの1Hシグナルは2.7ppmの13Cシグナルと相関している。図4 エチルベンゼンの2次元HSQCスペクトル
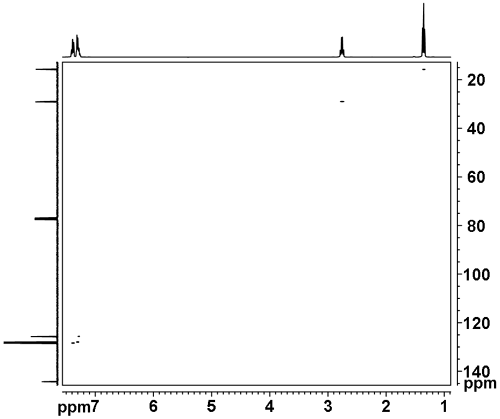
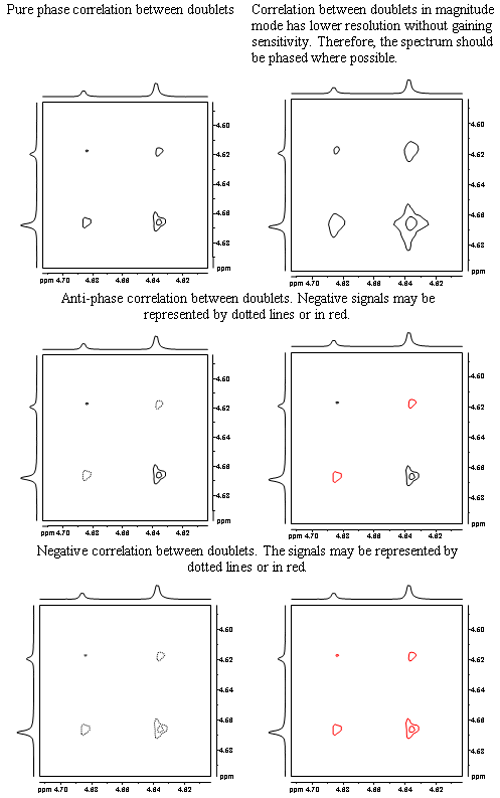
2次元スペクトルの信号は、必ずしも純粋な位相とは限りません。 HMBCや2D-INADEQUATEのように位相が単純に表現できない場合もあり、その場合はマグニチュードスペクトルがプロットされる。 しかし、マグニチュードスペクトルは純位相スペクトルに比べて分解能が犠牲になる(線を広げる窓関数と異なり、感度が上がらない)。 したがって、可能な限り、2次元スペクトルは位相付きであることが望ましい。 その結果、図5のように、純位相、逆位相、負位相の信号が得られる。 負の信号は、従来、点線または赤の輪郭で表されていた。 2つのダブレット間の相関に可能な位相
 。
。