3D Reconstruction

cd exercises/3d_reconstruction

コマンドによりkobuki_3d_reconstructionワールドでGazeboを立ち上げます

roslaunch ./launch/3d_reconstruction_ros.launch

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

どのように演習を実行するのですか。

演習を実行するには、ファイル MyAlgorithm.py を編集して、2 つのステレオ画像から 3 次元点を再構成するコードを挿入する必要があります。

ファイル MyAlgorithm.py の中です。

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Application Programming Interface

• self.getImage('left') – 左画像を得るため
• self.getImage('right') – 右画像を得るため
• self.point.PlotPoint(position, color) – 3d toolにポイントをプロットするため

Navigating GUI Interface

Mouse basedです。 ホールド&ドラッグで環境内を移動。 スクロールでズームインまたはズームアウト

キーボードベース。 環境内を移動するには、矢印キーを使用します。 W および S キーで拡大または縮小

Theory

コンピュータ ビジョンおよびコンピュータ グラフィックスでは、3D 再構成とは、オブジェクトの 3D プロファイルを決定し、プロファイル上の任意の点の 3D 座標を把握するプロセスです。 再構成は次のように実現できます：

• ハードウェアベース。 ハードウェアベースのアプローチでは、再構成タスクに特化したハードウェアを利用することが必要です。 構造化光、レーザー距離計、深度計、ラジオメトリック法などがその例です。

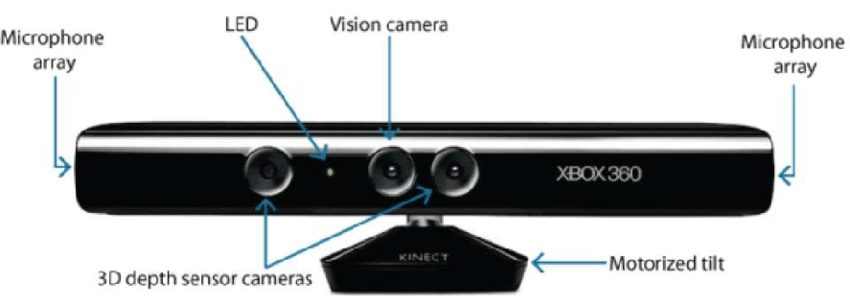
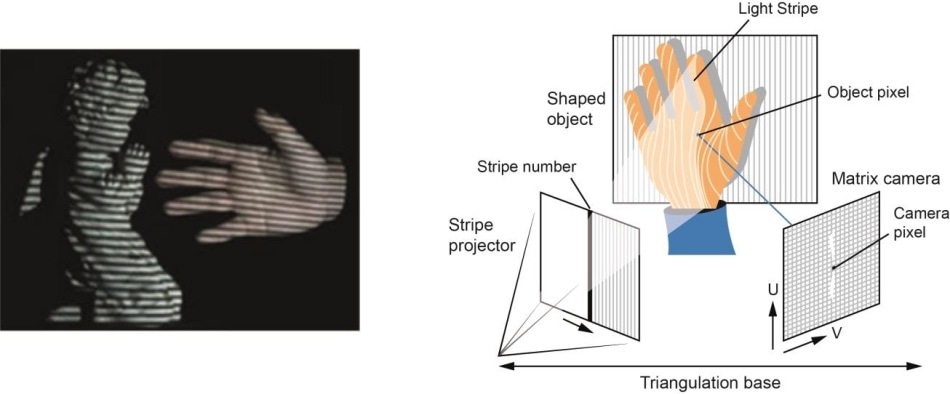
• Software Based（ソフトウェアベース）。 ソフトウェアベースのアプローチは、オブジェクトの3Dプロパティを決定するために、コンピュータの計算能力に依存しています。

この演習では、ソフトウェアベースのアプローチ、特にステレオビジョンの3D再構成を使用して3D再構成を行うことを主な目的としています。

Epipolar Geometry

二つのカメラが二つの異なる位置から3D場面を見るとき、画像点間の拘束につながる3D点とその2D画像への投影との間には多数の幾何的関係が存在する。 これらの性質と制約を研究する学問をエピポーラ幾何学と呼ぶ。 以下の画像と説明は、この考えを一般化したものと思われる：

3d 空間における点Xが、1つ目ではxで、2つ目ではx'で、2通りの画像になっているとする。

ここでxしか分からないとすると、対応する点x'はどのように拘束されるのかが気になるところである。 平面πはベースライン(カメラの中心を結ぶ線)とxで定義される光線によって決まる。 以上より、未知点x'に対応するレイはπ内にあることがわかるので、点x'はπと第二画像平面との交線l'上にあることになる。 この線をxに対応するエピポーラ線と呼ぶ。 この関係により、右画像中の点の探索空間が平面から直線に縮小される。

• エピポーラとは、カメラ中心を結ぶ線（基線）と画像平面が交わる点である。

• エピポーラ線は、エピポーラ平面と画像平面の交点です。

ステレオ再構成

ステレオ再構成とは、上記の3D再構成の特殊なケースで、2つの画像平面が互いに平行で、プロットしたい3D点から等距離である場合です。

この場合、両方の画像平面のエピポーラ線は同じで、平面の幅と平行になり、制約がより単純化されます。

3D再構成アルゴリズム

再構成アルゴリズムは3つのステップで構成されています。

1. 1つの画像平面から特徴点を検出する
2. 上で見つかった特徴点に対応する点を検出する
3. その点を3次元空間で三角測量する

一つ一つ見ていこう

特徴点検出

特徴点検出は広大な研究分野で、いくつかのアルゴリズムはすでに研究されています。 Harris Corner DetectionやShi-Tomasiアルゴリズムでは、固有値を使って良い特徴点を得ることができる。 しかし、問題は3D再構成のために多くの点が必要なことで、これらのアルゴリズムではそのような多くの特徴点を得ることができない。 次のアルゴリズムではエッジの検出に曖昧さが生じるかもしれない。 しかし、エッジを特徴点とすることで、問題は解決する。 エッジ検出アルゴリズムとして、Canny Edge Detection Algorithmがある。 このアルゴリズムは、エッジの生成という点では非常にシンプルで信頼性があります。

特徴点の抽出

エピポーラ制約の使用は、このアルゴリズムの時間複雑性を本当に単純化します。 一般的な3次元再構成問題では、1つの画像フレーム内のすべての点に対してエピポーラ線を生成し、そのサンプル空間内で他の画像フレーム内の対応点を探索する必要がある。 エピポーラ線の生成も非常に簡単で、左画像から右画像平面への平行線反復補間を行うだけです。

画像間の対応を調べるには、二乗差の和やエネルギー最小化など、多くのアルゴリズムがあります。 あまり深く考えずに、単純な相関フィルターを使用しても、このユースケースは十分です。

三角測量

簡単に言うと、画像平面上の 2 つの決定したポイントを使用して、3 次元ポイントがどこに位置するかを計算するだけです。 一般的なカメラでは、幾何学的・物理的な歪みがある場合があります。 そのため、その誤差を最小限に抑え、最も正確な3次元点投影を計算するためには、多くの数学が必要になります。

Hints

3d_reconstruction のエクササイズを解くのに役立つ簡単なヒントを提供します。 この演習では、OpenCV ライブラリが多用されています。

設定

演習の API を使用すると、簡単に画像を取得することができます。 また、画像を取得した後、3d再構成の際に含める必要のない余分な詳細があるため、画像に対してバイラテラルフィルタリングを行うのがよい方法です。 バイラテラルフィルタリングの効果については、図を参照してください。

相関の計算

OpenCVにはすでに相関フィルタが組み込まれており、matchTemplate()を通して呼び出すことができます。 エッジやコーナーのような極端なケースに注意してください。

1つの良い観察は、左のポイントは左の部分で対応し、右のポイントは右の部分で対応することです。

点のプロット

手動またはOpenCVベースの関数triangulatePointsは三角測量によく効きます。 ただ、代数的な実装を行う際に、すべての行列の形とサイズに注意してください。

単純な3D座標と均質な4D座標の違いに注意してください。 詳細については、このビデオを確認してください。

ユーザーによって実装が異なるため、GUI インターフェースで表示および表現できるようにするために、ユーザーは三角形の点のスケールとオフセットを調整する必要があるかもしれません。 3D座標ベクトルを500から1000の間の値でダウンスケールするのが効果的です。

Illustrations