Abelian groupとは、要素が交換する（すなわち、すべての要素
と
について
）グループのことである。 したがって、アーベル群は対称的な乗算表を持つ群に相当する。
すべての環状群はアーベル群であるが、アーベル群は必ずしも環状である必要はない。 Abelian groupのすべてのsubgroupはnormalである。 4349>
Wolfram Languageでは、関数AbelianGroupは次数
, 
, …の環状群の直積を表す。 しかし、任意の群位
の非同型Abelian有限群
の数は
 |
(1)
|
ここで、
は明瞭な素因数である。 then
 |
(2)
|
ここで 
は分割関数で、これは Wolfram Language で FiniteAbelianGroupCount として実装されているものです。 
, 2, …のときの
の値は1, 1, 1, 2, 1, 1, 3, 2, …である。 (OEIS A000688).
, 2, 3, … 非同型のAbelian群が存在する最小の次数は1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, …である.
。 (OEIS A046056)、ここで0は非同型Abelian, 群の不可能数（すなわち分割数の積でない）を表す。 欠番」は、13、17、19、23、26、29、31、34、37、38、39、41、43、46、…である。 (OEIS A046064)である。 次数の関数として増分的に最大となるアーベル群は、1、2、3、5、7、11、15、22、30、42、56、77、101、…である。 (OEIS A046054)であり、これは次数1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, …に対して発生する。 (OEIS A046055).
クロネッカー分解定理は、すべての有限アーベル群は素数乗群順の環状群の群直積として書くことができることを述べています。 有限群の群位が素数
の場合、群位
の単一のAbelian群（
と表記）が存在し、非Abelian群は存在しない。 群位が素数の2乗
の場合、2つのAbelian group (
と 
と表記)が存在する。 群順が素数の3乗
の場合、3つのAbelian group (
, 
, 
) となり合計5群存在することになる。 もし、2つの素数
と
の積であれば、群位
のアーベル群（
と表記）が正確に1つ存在することになる。
もう一つの興味深い結果は、
が群位
の非同型Abelian群の数を示すと、
 |
(3)
|
ここで
はRiemann zeta関数である。
位数
のAbelian群の数は、1、2、3、5、6、7、8、11、13、14、15、17、18、19、20、25、・・・で与えられる。 (OEIS A063966)で、
, 2, …となる。 Srinivasan (1973) はまた、
 |
(4)
|
ここで
 |
 |
 |
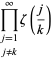(5)
|
 |
 |
 |
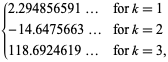(6)
|
(OEIS A021002, A084892, A084893), 
は再びリーマンのゼータ関数とする。 なお、Richert(1952)は
と間違っている。 和
は明示的に
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
 |
 |
 |
(9)
|
DeKoninck and Ivic (1980) は
 |
(10)
|
ここで
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A084911) は素数
上の積で、
は再び分割関数とする。
非同型の非アベリアン群の数の境界は、Neumann (1969) と Pyber (1993) によって与えられる。
アベリアン群を含む多くの数学ジョークがある (Renteln and Dundes 2005):
Q: 紫でコミュートするのは何でしょうか？ A: Abelian grape.
Q: What is lavender and commutes? A: Abelian semigrape.
Q: 紫色で通学路があり、限られた人にしか崇拝されていないものは何ですか？ A: 無限に崇拝されるアベルのブドウ
Q: 栄養価が高く、通約するものは何ですか？ A：アベルのスープ。