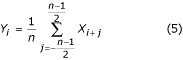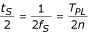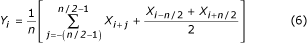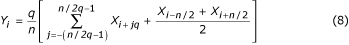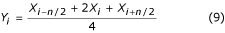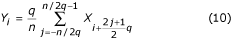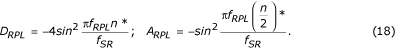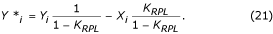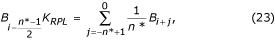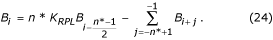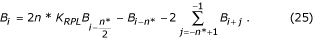Removal of power-line interference from ECG: a review of the subtraction procedure

PL 除去のサブトラクション法は、約20年前に初めて精緻化されたものである。 この方法は、PL周波数に隣接するECG成分には影響を与えない。 この理論的研究は基本的なPL周波数に対して行われたが、結論はその高調波に対しても有効であり、その結果、任意の干渉波形に対しても有効である。 この方法の効率は、増幅器が飽和しない限り、干渉の振幅に依存しない。 さらに、この方法は干渉の振幅や周波数が変化してもうまく対処できます。 この方法は、長年にわたって継続的に改良され、何千ものECG機器やコンピュータ支援システムに実装されています。 3682>

原理

減算法はもともとサンプリング周波数f Sの倍数で、PL周波数f PLと同期したハードウェアで適用される。 3682>

• ゼロに近い周波数帯域を持つECGセグメントは、適切な基準で連続的に検出される。 これらのセグメントは線形セグメントと呼ばれ、主にPQおよびTP間隔に見られるが、RおよびT波の十分に長い直線部分にも見られる。

• これらのセグメントのサンプルは移動平均され、すなわち、最初のゼロをf PLに設定した線形位相コムフィルタにかけられる。 したがって、フィルタリングされたサンプルは干渉を含まない。

• 補正と呼ばれる干渉振幅は、PL期間T PLにおける位相ロックされたサンプルnのそれぞれについて、汚染された（元の）ECG信号の対応するものからフィルタリングされたサンプルを減算することによって算出される。

• 得られた補正のセットは、線形セグメントにおいて継続的に更新され、非線形セグメント（通常はQRS複合体および高振幅T波の周辺）において、元のECG信号から干渉を減算するために使用される。 干渉は、誤差と方法の効率を評価するために、きれいなシミュレーションECG信号に加えられた。

  

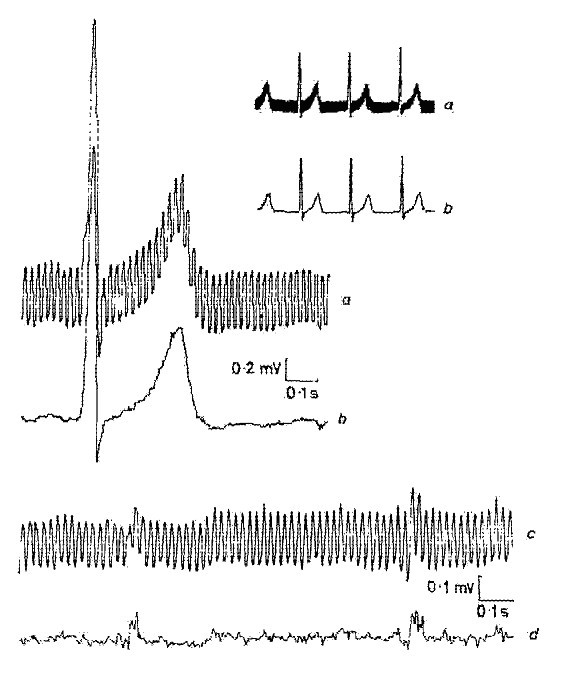
  サブトラクション手順によって得られた最初の結果の1つである。

  線形基準

  線形基準Crは、通常、信号の2次差分に相当する（線形性の数学的評価）。 最初のCrは次のように定義される。 6つの連続した第1差分FD i は、1T PL間隔で置かれた信号サンプルX i を使って計算される：

  FD i = X i+n – X i , for i = 1 … 6 (1)

  n = f S /f PL なら、第1差分のPL干渉は抑制されます。 この場合、当初は定格f PL = 50 Hz、f S = 250 Hzで開発された手順なので、n = 5となる。 さらに、FD maxの最大値とFD minの最小値をとってCrを決定する：

  Cr = | FD max – FD min | <M, (2)

  ここでMは閾値である。

  典型的な線形および非線形セグメントを図2に示す。 実際のECG信号（トレースa）には干渉が重畳している（トレースb）。 線形セグメントには、低周波信号と電力線周波数成分が含まれる。 図2

  

  実ECG信号における典型的な線形セグメントと非線形セグメント。

  

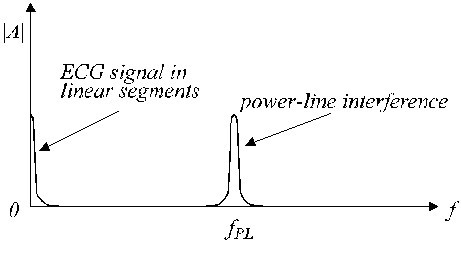
  線形セグメントの近似周波数スペクトル

  この基準は正確に作用するが、比較的遅い実装なのでリアルタイムではほとんど適用されない。 この欠点はChristovとDotsinskyによって克服され、わずか2つの後続の差の修正された基準を使用します。

  Cr = | FDi+1- FD i | <M. (3)

  式(3)を満たさない最初のサンプルは、非線形のセグメントの始まりに関連している。 非線型から線型への移行では、線型セグメントの早期検出を避けるために、式(3)をn回連続して満たす必要がある。 この基準は、f S = 400 Hz、n = 8の実時間で実施される。

  その後、DotsinskyとDaskalovは、基準を2つの非連続の差として定義した：

  Cr = |FDi+k- FD i | <M, for k >1 (4)

  このアプローチにより線形から非線形への移行はより正確に行われるようになった。

  PL振幅変動の補償

  補正の更新頻度が高いほど、PLの振幅変動の補償は良好になる。 したがって、線形基準閾値Mは、理想的な線形信号から逸脱するいくつかのセグメントを平均化することによって生じる誤差が、Mによって補正の散発的な更新が開始された場合に生じる誤差よりも小さくなるように、適度に制限の少ないものでなければならない。 当初、M は 160 μV に固定されていた。 その後、M=150μVとM=100μVが発見された。

  Linear Filtering

  PL干渉の1周期で奇数サンプル数n=2m+1に対して、フィルタリングした値：

  

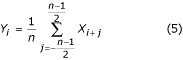
  はフィルタリングしない値と位相共起であった。

  偶数n=2mの場合、2つの値はサンプル周期の半分だけ位相がずれている。

  

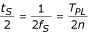
  ただし、

  

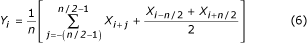
  式により同相の一致になる。 n/qが奇数か偶数かによって、それぞれ(7)式、(8)式を用います。

  

  

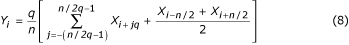
  q=n/2で最大サンプル数減少の特別なケースが発生します。 対応する式：

  

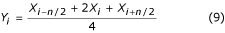
  は「3点」フィルタと呼ばれる。 式(8)に加えて、qが偶数の場合は、以下の式

  

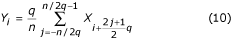
  を適用することも可能である。 q=n/2の場合、フィルタは「2点」となり、次式で表される：

  

  干渉の1周期中のサンプル数が減ると、櫛形フィルタのローブの急勾配が強調され、計算時間が短縮される。 しかし、これらの「利点」は、第3次高調波が大量に存在する場合にナイキスト規則に違反しないように、慎重に評価する必要があります。 その他の高調波は考慮されていません。なぜなら、最も高い奇数調波は通常100～150 Hzの範囲でカットオフしたローパスフィルタで抑制され、偶数調波は発電所の発電機の精密な極製造のため実質的に存在しないためです。 実際には、それ以上の偏差が発生することが多い。 Kumaravelらは3%のばらつきがあると報告している。 McManusらは、Common Standards for Electrocardiography (CSE)のデータベースから取得した記録と重ね合わせた干渉周波数にかなりの変化があることを発見した。 この複雑さは、f PLの連続的なハードウェア測定によって偏差を検出し、定格(R)値、t RS = T RPL /nの周辺でサンプル間隔t Sをわずかに調整することによって補正すれば回避できる(ここでは、T RPL = 20 msはf RPL = 50 Hzの定格T PLである)。 f PL 、偏差49.5～50.1Hzの場合、t Sの変動は1％の範囲であり、その結果、自動ECG分類に通常使用されるパラメータの許容測定精度を超える誤差は発生しない。

  第1のアプローチは、期間T PLにおけるシーケンスS k (k = 1, 2・・・n)のそれぞれの第1サンプルS 1のトリガーを、任意に選択したが一定のPL電圧の振幅を伴って行うことを連想させる。 次のサンプルS k (k = 2…n) は，t S = T RTL /n で得られるt S の間隔で配置されます。 50Hz、n = 5の場合、t S = 4msとなります。 Dotsinsky と Daskalov は、この方法で発生する 2 種類の誤差を研究しています。 1 つは，サンプル間の不規則性によるもので，f RPL の周囲で 1%の偏差がある場合，f S = 400 Hz で 1%，f S = 250 Hz で 1.2% に達する可能性がある． 2つ目の誤差は3%を超えず，これはフィルタリングされたサンプルの位置が追加でずれた結果です． 現在進行中の期間T PLを測定し、nで割る。 得られたt Sは、その後のT PLで使用される。

  手順の効率評価

  減算手順の例を図4と図5に示す。 ECG信号はAmerican Heart Associationのデータベースから取得したものである。 信号は60Hz（米国でのPL周波数）の干渉を抑制するためにノッチフィルタがかけられている。 次に、信号は50Hzの干渉と混合され、200μVs-1のスルーレートで0から3.2mVp-pまで振幅変調される。 トレースは次のように識別されます：i) 入力信号、ii) 合成された干渉、iii) 混合信号、iv) 処理された信号、v) 原信号と処理信号の差、vi) ズームされた差。 実際には、捨てられた成分には筋電図（EMG）やその他のノイズも含まれる。 3682>

  

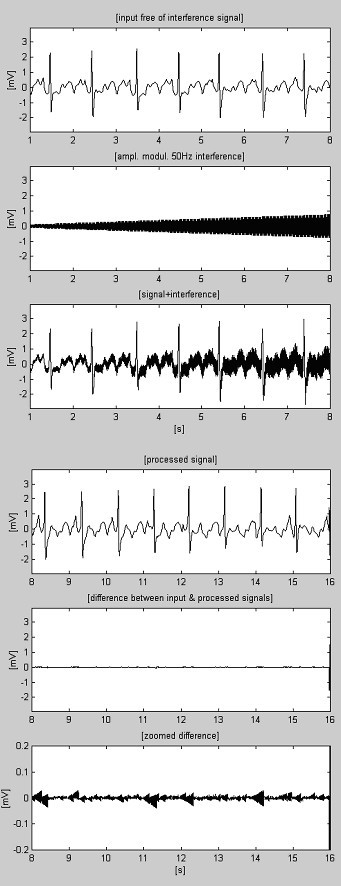
  AHA 3004d1 recordingを処理した信号。

  

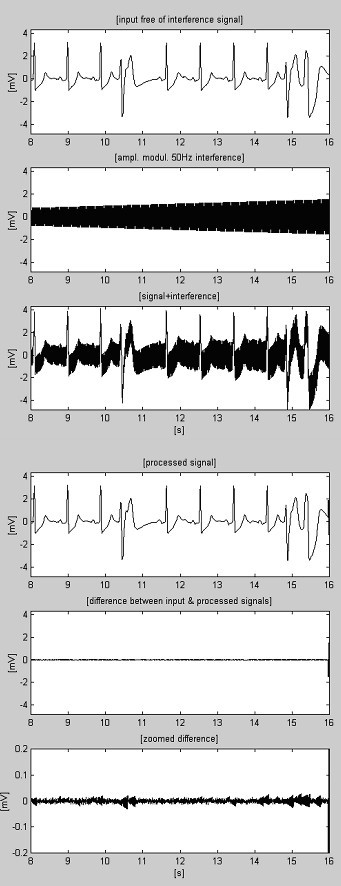
  AHA 6007d1収録のものを加工しました。

  2つの信号は、干渉のみに関するサブトラクション手順の効率を評価するために使用されます。 最初のものは、我々自身のデータベースから取られたもので、条件付きで「クリーン」と呼ばれるものである（図6）。 その結果、入力信号と処理された信号の間に、入力に含まれるノイズに起因する小さな差異が視覚的に確認されました。 この結果は、外乱を含まない2番目の合成信号で検証されます（図7）。 見てわかるように、歪みは発生していない。 同じ合成信号に干渉を重畳して処理したもの（図8）。 3682>

  

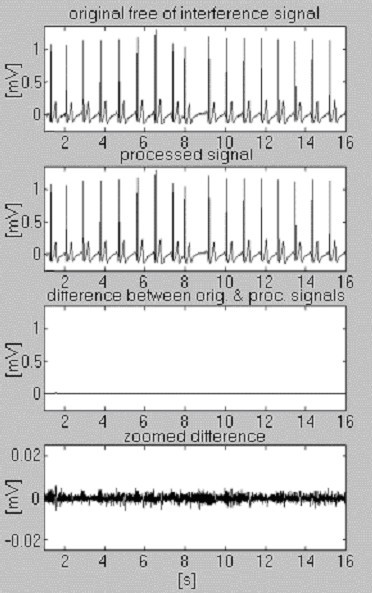
  条件付き「クリーン」信号の処理。

  

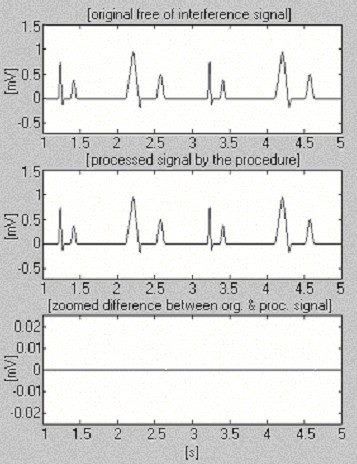
  合成された信号を処理する。

  

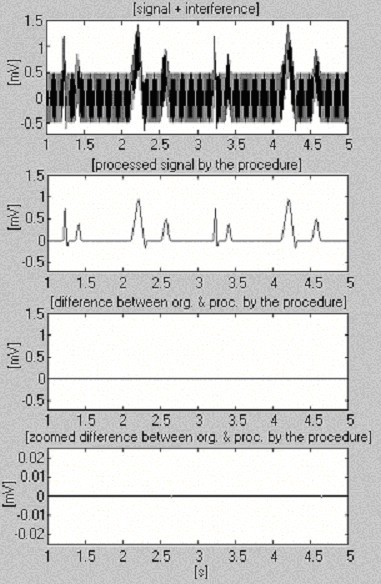
  処理した合成信号+干渉を表示します。

  EMGノイズの影響

  EMGノイズが大きく、線形セグメント検出が阻害されることがある。 結果として、干渉振幅の最後の変化に対応しない不正確な補正は、エラーを引き起こす（図9の11秒と14秒の間の残留ノイズを参照）

  

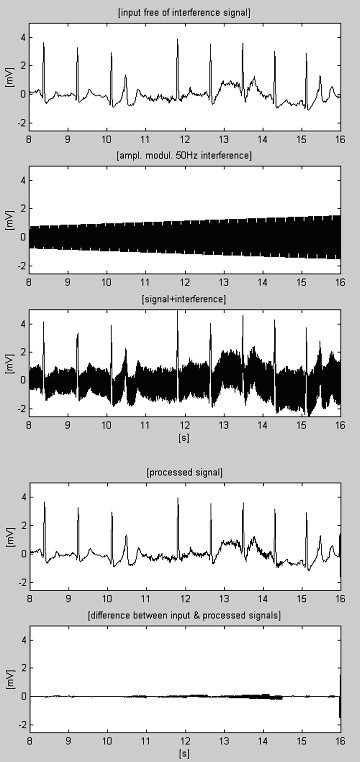
  処理済みのECG信号+EMGノイズ+干渉。

  手順に対するEMGノイズの影響を抑制するための非常に簡単なアプローチは、信号の進行中の部分が無条件に平均化される追加の並列バッファを導入することである。 このバッファは、正確な直線性の検出に使用される。 図10と図11は、パラレルバッファを使用しない場合と使用した場合の結果の比較である。 a’のトレースは、干渉とEMGノイズが混ざったECG信号である。 図 10 の b と図 11 の c は、線形セグメントから非 線形セグメントへの遷移（オンオフ関数）を示している。 見てわかるように、図10の平均化された信号部分は非常に限定的である。 その結果、処理効率が低下している（図10c、10d。 これに対し、パラレルバッファでは、長い線形セグメントを検出することができ（図11c）、処理された信号の残留ノイズは低い（図11d. しかし、ノイズの一部は補正計算に参加するため、完全に抑制されているわけではない。

  

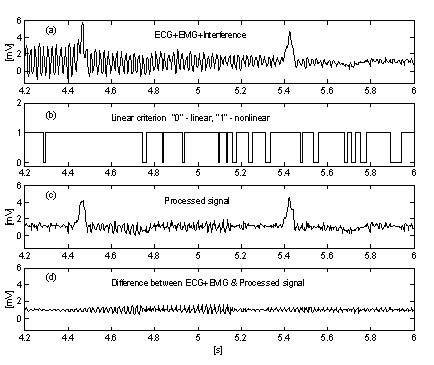
  パラレルバッファを使わない干渉+EMGノイズの減算処理。

  

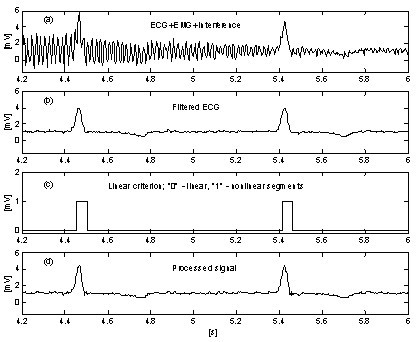
  パラレルバッファを使用した干渉+EMGノイズの差し引き。

  EMGノイズ抑制のさらなる改善は、適応的閾値Mを用いることによってChristovによって得られ、これは、Rt＝S NL／SFとして定義されるノイズ／信号比Rtに関して計算され、ノイズレベルS NLは、検討中のRR間隔にほぼ相当するエピークS Fにおける非線形セグメントの要約幅に等しくなる。 きれいなECG（図12a）およびEMGノイズで汚染された同じ信号（図12b）に対するM＝150μVの基準での直線性検索は、異なるS NL 、（図12cと12d）を示している。 この手法は MATLAB 環境で開発された。 初期閾値Mは30μVに等しく選ばれる。 その後、Rtが10%になるまで徐々に増加させ、その後、減算処理を開始する。 Rt≦0.1の値は、「QRS幅とそのRR間隔」の比によって示唆され、通常10％前後である。 干渉とEMGノイズの両方の除去は、M＝420μVを使用した図13b及び13dで観察することができる。 比較のために、「クリーン」ECG信号は、M＝35μVで処理される（図13a及び13c）＜3682＞＜642＞＜4916＞＜2186＞図12＜3829＞＜642＞＜3054＞図12＜3049＞＜5155＞＜642＞＜5179＞ノイズレベルSNL（痕跡c及びd）それぞれ「クリーン」ECG信号（痕跡a）及び電磁石汚染信号（痕跡b）において、ノイズがある。

  

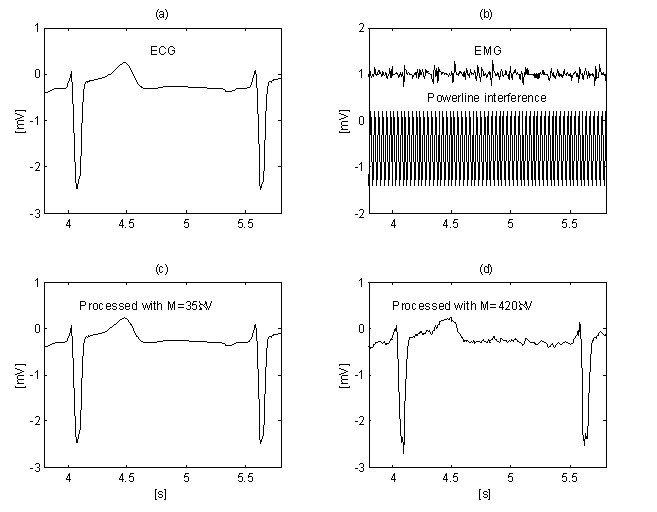
  適応閾値Mによる干渉＋EMGノイズ抑制：M＝35μVで処理した「クリーンシグナル」（a）（c）とM＝420μVの手順を適用した汚染シグナル」（b）（d）。

  心房細動と心室細動の患者では、線形セグメントを規則的に見つけることはできない。 しかし、細動の検出には波形の完全な保存は必要ないため、あらゆる種類の従来のフィルタが適用できます。

  高分解能ECGにおける干渉抑制

  低振幅で比較的低い周波数のHis波は線形セグメントで識別できないため、減算手順は体表面His-ECGに直接適用できません。 従って、実際にはHis波は抑制されるか、信号から除去されることになる。 EMGノイズは通常、表面His波に比べ、振幅が大きく、周波数も非常に高い。 そのため、単純に閾値Mを変更するだけでは、線形セグメントと非線形セグメントの区別がつかない。

  Bazhina et al.では、以下のような修正を施した。 QRS複合体の前に検出された非線形のセグメントの開始点を100ms左にシフトすることで、His波領域をデフォルトで非線形のセグメントとして定義している（図14）。

  

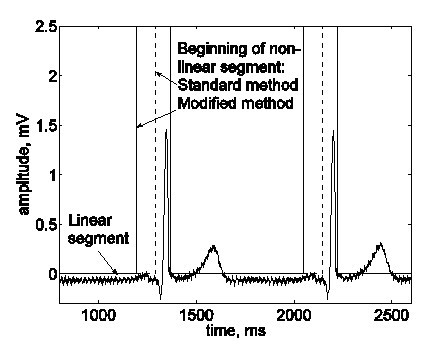
  QRSコンプレックスを含む非線形のセグメントの開始は、デフォルトで左に100 msシフトし、His束波の出現が期待されるゾーンが含まれるようになった。

  減算法と他の3つの方法：ノッチフィルター、スペクトル補間、回帰減算は、元の信号の最小限の歪みに対してテストされました。 Barattaらが線形セグメントのノイズ推定に同様の概念を用いていることから、減算法と回帰減算法が最適であることが判明した。 3682>

  Case of battery supplied devices and computer aided ECG systems

  The hardware measurement of f PL, necessary for compensation of the interference frequency modulation is not feasible in battery supplied devices and some computer aided ECG systems.In the battery supplied devices and in a segment.This system is not possible. DotsinskyとStoyanovは、振幅が一定の干渉の周波数変化の範囲について、同期サンプリングを使用せずに残留部分が許容レベルまで制限されることを研究しました。 彼らは，20μVp-p以下の残留干渉が，i）干渉振幅≦0.4mVp-p，ii）速度≦0.0125Hzs-1の周波数変化による手順で得られることを見いだした。 電源に対するこのような要件はしばしば超過し得るので、ソフトウェアによる干渉測定が開発された。

  ECG信号はまず49-51Hzのバンドパスフィルタによって処理される。 干渉の正方向の傾きから、ゼロ線の下と上に位置する2つの隣接するサンプルBr LとBr Rの振幅が測定される(図15)。 図15

  

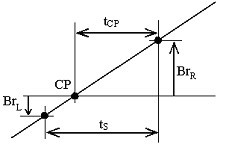
  Interference zero crossing.The distance, t CP , between the crossing point CP and the right sample, Br R , is compute continuously by:

  The interference zero crossing.The 距離は連続的に計算される。

  

  TPLが変化した場合、t Sは

  

  を用いて再定義されます。この方法はMATLAB環境で実施されました。 サンプリング周波数f S = 500 Hz、f RPL = 50 Hzの場合、nは10に等しい。 図16は、2mVp-pの一定振幅で、8秒間に1Hzずつ極めて高速に変化する干渉によって混合された後の1mVのECG信号（最初のトレース）を示している。 得られた効率を評価するために、同期サンプリングなしのズームされた差分（最後のトレース）も示されている。

  

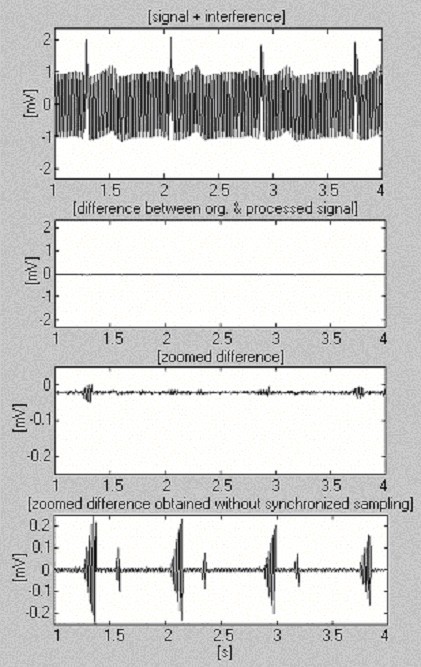
  ソフトウェア電力線周波数測定による減算手順。

  次に取るべき論理的なステップは、i) ECG 装置の定格 t S を維持し、ii) 妨害を除去するために、現在測定中の f PL に従って信号を再度サンプリングし、iii) 定格 t S に戻すことです。 このようなアプローチの最初の結果は非常に有望である。 このように，変動するf PLのソフトウェア補償と，50または60 Hzのf RPLの自動調整を含む減算手順の計器への完全な実装は，ハードウェア回路と対応するソフトウェアに関係なく完了することになります。

  定格PL周波数への自動適応

  50および60Hz環境での代替干渉減算のための共通のプログラムは、非多重サンプリング、すなわち実数nにつながります。 逆の場合，f S = 360 Hz では，n = 7.2 が必要である。 3682>

  fSの変更を必要としない非常にシンプルな解決策が、DotsinskyとStoyanovによって発見されました。 この方法は、干渉の1周期T PLに櫛形フィルタを適用するものである。 そのため、プログラムの実行速度が速くなります。 一般に、nはk > 1周期全体から取ることができる。 t S = 2 ms (f S = 500 Hz) とf RPL = 50 Hzの場合、式（14）を満たすkの最小値はk = 1であるが、60 Hzの場合、kは3である。 20Hzと40Hzのサブハーモニクスに関連するゼロも現れますが、手順には影響しません。 したがって、両方の干渉に対応するためには、nを10（k=1）と25（k=3）の間で切り替えれば十分です。 この目的のために、2つのデジタル・バンドパス・フィルターが入力信号をチェックします。 図17は、干渉と重なる周波数帯域のフィルタが、他のフィルタよりも一桁高い出力信号を生成することを示している。

  

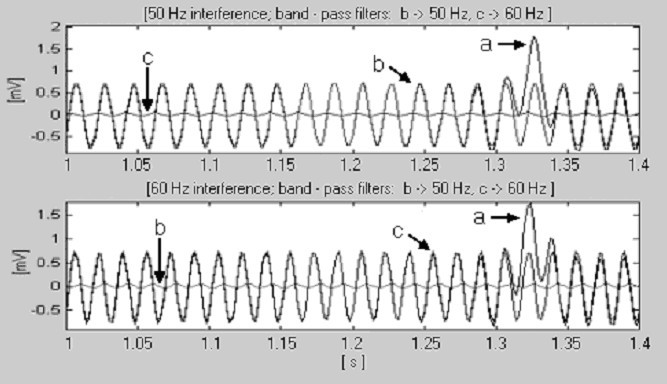
  定格電力線周波数の検出、a）QRS複合体の一部、b）50Hz干渉と、c）60Hzの干渉。

  理論的手順の開発

  減算手順の理論は、Mihov 、Levkov and Mihov 、およびMihovらによってさらに開発されました。 彼らは、同期AD変換を用いずに、干渉周波数変動を含む非多重サンプリングのほぼすべての場合の問題を克服しうる一般化された構造で実装された4種類のフィルタを提案した。

  マルチプルサンプリングにおけるいわゆるD-フィルタは、式（2）のCrのように定義され、1T PL間隔で配置されたFDで2番目の差D i が求められる。

  D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)

  Dフィルタの伝達関数はf = 0およびf = f PL Hzでゼロとなり、図では50 Hzと等しく示されている。 3682>

  

  fPL = 50 HzのD-フィルタの伝達関数

  K-フィルタは式（5）と（6）で示される移動平均を表現している。 その伝達関数は、奇数多重度の場合、n＝5について図19に示す。

  

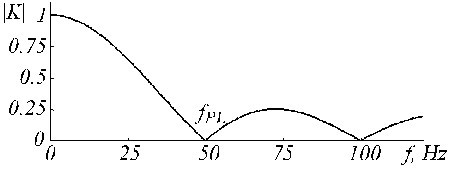
  fPL＝50Hz、n＝5についてのKフィルタの伝達関数を示す。

  干渉成分の継続計算に使用する式：

  B i = X i – Y i (16)

  実際には、（1K）-フィルタというデジタルフィルタが定義されています。

  さらに、フィルターは非多重サンプリング用に再定義され、f S = 250 Hzとf RPL = 60 Hzを組み合わせて、ソフトウェアの改良を説明するために考慮されます。

  伝達関数ゼロを維持するために、Dフィルターは、f = 0でゼロ、f = f RPLでD RPLのゲインが同じ周波数のDフィルターのゲインと同じ、f RPLの補正フィルターで減算されなければならないのです。 補正フィルタの合成は，式:

  

  ここで，(n/2)*はn/2の丸められた値である。

  ARLはf = f RPLに対する補助フィルタの利得なので，補正フィルタは比D RPL /A RPLで掛け合わされる。 D RPLとA RPLは、対応する伝達関数を使って、あらかじめ

  

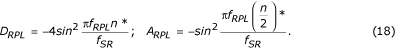
  最後に、補正D*フィルタは

  

  として示され、図20では、トレース ‘c’ として示されており、トレース ‘a’ と ‘b’ はそれぞれDフィルタおよび補正フィルタである。

  

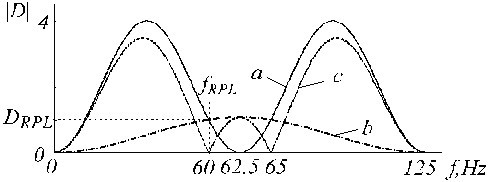
  a）D-フィルタ、b）補助補正フィルタおよびc）補正D-フィルタの転送関数。

  K-filterの伝達関数は、f = f RPLでゼロ、f = 0でユニティゲイン、線形位相応答を保持する必要があります。 K-filterの補正の手順は前述と同様である。 補助フィルタは補正計算に使用する式で与えられる：

  A i = X i – Y i , (20)

  フィルタゲインはf = f RPLに対して1 – K RPLに等しく，K RPLは同じ周波数f RPLに対するKフィルタのゲインである。 補助フィルタは，K RPL /(1 – K RPL )を掛けて，Kフィルタから減算します。 補正後のK*-フィルタの式は次のようになる：

  

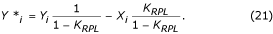
  定数K RPLは、奇数または偶数の多重度の場合、それぞれ:

  

  により推定することができる。

  Kフィルタ補正の一例を図21に示す。トレース’a’、’b’、’c’は、主Kフィルタ、補助フィルタ、および補正後のK*フィルタを表す。

  

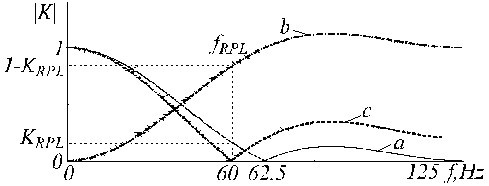
  a）Kフィルター、b）補助補正フィルター、c）補正Kフィルターの伝達関数を示している。

  非多重サンプリングの場合、進行中のECGサンプルと、通常は一時的な先入れ先出し（FIFO）バッファにある干渉成分B i（式16）の間に位相差が発生する。 したがって、B iは、非線形セグメント中にECGサンプルから減算されるように修正されなければならない。 この補正手順は比較的複雑である。 図22は、一時的なバッファの内容を示している。 現在の干渉サンプルB i-n *は復元されたサンプルB iと一致しない。 両者の位相差を補正するために、その振幅を再計算しなければならない。 これは，f = f RPL に対して線形位相応答と単一ゲインを持つ新しいフィルタ（B-フィルタと呼ぶ）によって達成される． これは既知のK-フィルターから合成され、干渉周期に等しいウィンドウを持つ。 奇数n*の場合、次のように記述できる：

  

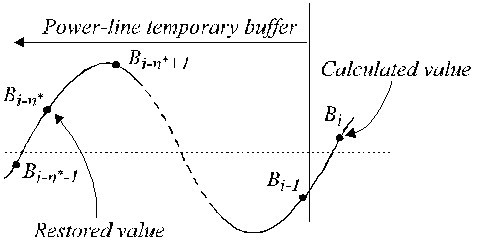
  一時バッファに復元された値。

  

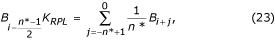
  ここで、K RPLは式（22）で与えられる平均化フィルタの干渉に対するゲインである。

  復元されたバッファ値B iは、

  

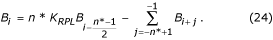
  偶数n*の場合：

  

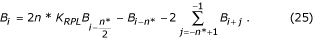
  Bフィルタの伝達関数は、図1に示すようになる。 23.

  

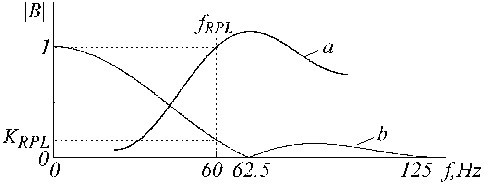
  a）B-フィルターとb）既知のK-フィルターの伝達関数

  一般化した構造を図に示している。 24では、減算手順のモジュールは以下の通りである：

  

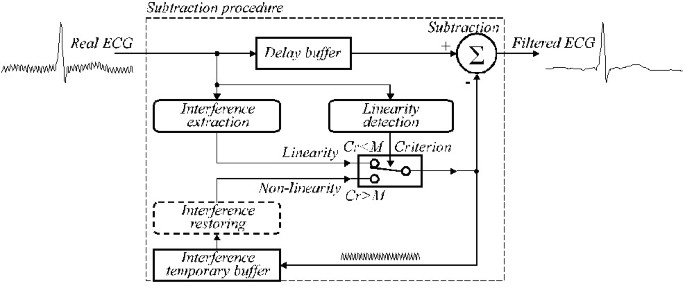
  減算手順の一般的構造

  • 直線性検出を実施する。 各信号サンプル近傍の直線性を評価するためにD-filterを適用する。

  • 干渉抽出。 (1-K)-フィルターを用いて干渉成分を計算する。

  • 判定基準。 条件Cr <MがSubtractionに抽出または復元したPL干渉を送る。

  • 干渉の一時バッファ。 非線形セグメントで補正として使用される抽出または復元された干渉成分は、電力線干渉の進行中の位相とロックされた位置に保存されます。

  • Interference restoring. 非多重サンプリングの場合、非線形セグメントの入力信号サンプルから減算される真の補正値を復元するために、Bフィルタが呼び出されます。 D-フィルターや(1-K)フィルターで発生する遅延を補うもので、準リアルタイムで実行される場合には必須。

  • Subtraction (減算)。 抽出または復元された干渉値は、「クリーン」なECG信号を出力するために、遅延入力信号から減算されます。 非直線性の場合、干渉抽出と減算の両方がK-フィルタを実装しています。

  一般化された構造に従って改良されたアルゴリズムは、オフラインでテストされています。 fS＝250Hz、fRPL＝60Hzの結果を図25に示す。

  

  fRPL＝60Hz、fS＝250Hzでの非多重サンプリングの例

  。