Katso Uusimmat artikkelit

Abstract

Valo kulkee tyhjiössä nopeudella c riippumatta valonlähteen liikkeestä tai tarkkailijan viitekehyksestä. Näin ollen valon kulkeminen valonlähteestä avaruudessa olevaan havaitsijaan vaatii jonkin verran aikaa, jolloin valon lähettäminen ja lähetetyn valon havaitseminen eivät ole samanaikaisia. Näiden näkökohtien perusteella ehdotetaan menetelmää havaitsijan absoluuttisen nopeuden mittaamiseksi, jota voitaisiin käyttää avaruusaluksen liiketilan määrittämiseen suljetusta hytistä käsin. Tässä tutkimuksessa esitellään myös uusi selitys Lorentzin muunnokselle.

Avainsanat

koordinaatisto, referenssijärjestelmä, liike, absoluuttinen nopeus, suhteellisuusteoria, Lorentzin muunnos, aika, avaruus, havainnoitsija, valonlähde
Seuraavassa analyysissä esitellään käytännöllinen lähestymistapa havainnoitsijan absoluuttisen nopeuden mittaamiseen, jota voitaisiin käyttää avaruusaluksen liiketilan määrittämiseen suljetusta hytin sisältä. Absoluuttisen nopeuden käsitteellä viitataan yleensä fysikaalisen systeemin eri objektien vakiomuotoiseen yhtenäiseen nopeuteen suhteessa oletettuun liikkumattomaan tilaan, joka on olemassa sen sisältämistä fysikaalisista objekteista riippumatta (ts. absoluuttinen tila). Tässä esitellään jäykkään kinematiikkaan perustuva lähestymistapa, jolla osoitetaan, että havaitsijan absoluuttinen nopeus voidaan määrittää siitä, että valo kulkee tyhjiössä nopeudella c riippumatta valonlähteen tai havaitsijan viitekehyksen liikkeestä. Näin ollen valon kulkeminen valonlähteestä havaitsijalle avaruudessa vaatii jonkin verran aikaa, jolloin valon lähettäminen ja lähetetyn valon havaitseminen eivät ole samanaikaisia.
Ehdotetussa analyysissä esitämme ensin seuraavat konventiot tarkasteltaville koordinaattijärjestelmille. Oletamme, että kartesiolainen koordinaatisto koostuu kolmesta pareittain kohtisuorasta akselista, jotka lähtevät pisteestä (0,0,0), jossa mikä tahansa piste P avaruudessa voidaan määritellä sen koordinaateilla x-, y- ja z-akselilla, joita edustaa järjestetty reaalilukupari (x,y,z). Inertiavertailujärjestelmän S oletetaan edustavan avaruuden suorakulmaista koordinaatistoa (x,y,z), jonka alkupiste on O. Sarja vakiokelloja (joita nimitetään S-kelloiksi) sijaitsee S:n paikoillaan olevissa pisteissä. S-kellot on kalibroitu vastavuoroisesti (eli ne antavat samanarvoisia lukemia samalla hetkellä) valosignaalin lähettämisen ja vastaanottamisen perusteella. Tarkemmin sanottuna kellosta A heijastetaan kellosta B valonsäde kelloon B, joka heijastuu kellosta B takaisin kelloon A ja saapuu kelloon A kellonaikana tA’. Jos , molemmat kellot on kalibroitu. Mille tahansa tapahtumalle, joka sijaitsee koordinaateissa x,y,z, sen aikakoordinaatti t annetaan tapahtumaan liittyvän S-kellon lukeman perusteella. Vastaavasti luodaan toinen inertiaviitejärjestelmä S’, joka perustuu toiseen avaruuden suorakulmaiseen koordinaatistoon (x’,y’,z’), jonka alkupiste on O’, ja toinen sarja toisiaan kalibroituja standardikelloja (S’-kellot) sijaitsee viitejärjestelmän S’ paikoillaan olevissa pisteissä. Mille tahansa tapahtumalle, joka sijaitsee koordinaateissa x’,y’,z’, sen aikakoordinaatti t’ annetaan tapahtumaan liittyvän S’ -kellon lukeman perusteella.
Koska avaruus- ja aikakoordinaattien origot sekä koordinaattiakseleiden suunnat voidaan valita pitkälti mielivaltaisesti, tässä käytetyt S:n ja S’:n väliset suhteet perustuvat seuraaviin konventioihin, joita on sovellettu yksinkertaisuuden vuoksi.
(1) Tietyllä ajanhetkellä molempien järjestelmien origot ja koordinaattiakselit ovat päällekkäin, ja kellot, jotka sijaitsevat O:ssa ja O’:ssa, asetetaan nollaan, ts, .
.
(2) x- ja x’ -akselit ovat yhteneväiset S:n ja S’:n suhteellisen liikkeen suunnassa; näin ollen x ja x’ ovat koko ajan yhteneväiset, kun taas y ja y’ sekä z ja z’ ovat samansuuntaiset.
(3) S’ liikkuu S:n +x-suunnan suuntaisesti.
Ehdotettu analyysi perustuu perusperiaatteeseen, jonka mukaan valo tyhjiössä kulkee vakionopeudella c riippumatta siitä, liikkuukö havaitsija vai valonlähde. Näin ollen tässä määritellään havaitsijan absoluuttinen nopeus U, jonka oletetaan olevan lineaarinen ja tasainen, seuraavasti: , missä f(φ) edustaa valosignaalin suunnan ja U:n suunnan välisen geometrisen suhteen funktiota, jota tässä merkitään φ:llä.
Ehdotetussa analyysissä esitetään kaksi uutta selitystä ajan ja pituuden suhteellisuudelle, jotka eroavat Einsteinin selityksistä (ks. ”Liikkuvien kappaleiden elektrodynamiikasta”). Nämä selitykset esitellään seuraavissa kappaleissa.

Ajan suhteellisuus

Valon äärellisestä nopeudesta johtuen valon kulkemiseen valonlähteestä avaruudessa olevaan havaitsijaan tarvitaan jonkin verran aikaa. Tästä voidaan päätellä, että valon lähettäminen ja valon havaitseminen eivät voi olla samanaikaisia. Valon nopeuden pysyvyyden ja kuvassa 1 esitettyjen olosuhteiden perusteella määritellään seuraavat tekijät. Valonlähteen ja havaitsijan sijainnit hetkellä , jolloin valonlähde lähettää valoa (merkitään tapahtumaksi R), ovat A ja H0. Valon etenemisen aikana ajasta paikkaan havaitsija kulkee matkan U∙T paikasta H0 paikkaan H, jolloin havaitsija vastaanottaa lähetetyn valon. Vastaavasti määrittelemme etäisyydeksi l havainnoitsijan valosignaalin vastaanotossa olevan sijainnin ja valonlähteen sijainnin välillä, kun valoa lähetetään . Valon nopeuden pysyvyyden vuoksi . Etäisyys vastaa U∙T. Lopuksi määritellään etäisyydeksi l0 havaitsijan sijainnin ja valonlähteen sijainnin välillä. Tässä esitämme tarkastelun havaitsijan sijainnista , jolla ei aiemmin ajateltu olevan fysikaalista merkitystä. Jos havaitsijan ja valonlähteen liiketilat ovat ekvivalentteja, saadaan l0, jolloin U voidaan laskea ,kuvassa 1 esitettyjen kolmiosuhteiden avulla.
Tässä työssä tapahtuman aika mitataan seuraavalla menetelmällä. Sekä havaitsija että kello sijoitetaan alkupisteeseen. Kun tapahtumaa kuvaava valosignaali saapuu havaitsijalle, valon saapumisaika vastaa kellon näyttämää aikaa. Vastaavuuden etuna on, että se liittyy aina kelloa käyttävän havaitsijan sijaintiin. Kuten kuvasta 1 nähdään, avaruuspiste O3 voidaan määritellä valonlähteen sijainnin perusteella, kun se lähettää valoa kohdassa , ja avaruuspiste O2 voidaan määritellä havaitsijan sijainnin perusteella, kun se vastaanottaa valoa kohdassa . Ei ole kuitenkaan ilmeistä, millä tavoin määritellään avaruuspiste O1, jossa havaitsija sijaitsee, kun valonlähde lähettää valoa kohdassa . Tämän ongelman ratkaisemiseksi otetaan käyttöön absoluuttisen levon (ts. ) ja absoluuttisen liikkeen (ts. ) käsitteet. Korvaamme yhden liikkuvan havaitsijan pisteissä H0 ja H kahdella havaitsijalla H1 ja H2, jotka ovat levossa avaruuspisteissä O1 ja O2, kun taas valonlähde A on levossa avaruuspisteessä O3. Kumpikin havaitsija ja valonlähde käyttävät kalibroituja standardikelloja, ja A lähettää valosignaalin klo , jota kutsutaan tapahtumaksi R0. Kun havaitsija H1 vastaanottaa valosignaalin, joka kulkee nopeudella c, kellon lukema on T0, ja kun H2 vastaanottaa sen, lukema on T. Näin ollen etäisyydet ja voidaan määritellä valosignaalin kulkuaikojen perusteella seuraavasti:
, (1)
ja
. (2)
Kuvassa 1 esitettyjen kolmiosuhteiden mukaisesti tapahtuman R0 muunnos havaitsijoiden H1 ja H2 välillä saadaan seuraavasti:
(3)
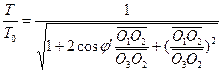(4)
Tässä on suoran O3O1 ja x-akselin välinen kulma ja on suoran O3O2 ja x-akselin välinen kulma.
Palataan nyt yhden liikkuvan havaitsijan tilanteeseen ja oletetaan, että järjestelmässä S sekä havaitsija H että valonlähde A käyttävät kalibroitua standardikelloa. Tapahtumahetkellä R valonlähde A on avaruuspisteessä O3 ja havaitsija H on pisteessä O1. Hetki, jolloin valosignaali saavuttaa avaruuspisteen O1, vastaa S-kellon lukemaa T0. Kun havaitsija H vastaanottaa valosignaalin, lukema on T, ja H on pisteessä O2.
H ei tietenkään voi havaita tapahtumaa R pisteessä O1. Tämän ongelman ratkaisemiseksi toinen havaitsija H-is sijoitetaan järjestelmään S pisteeseen O1, joka vastaa , jossa H-:n sijaintia käytetään määrittämään avaruuspiste O1. Tällöin tapahtuman R muunnos havaitsijoiden H- ja H välillä saadaan yhtälön (3) avulla seuraavasti.
(5)
Siten yhtälöt (3) ja (4) voidaan kirjoittaa uudelleen seuraavasti:
(6)
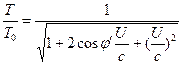(7)
e huomaa myös, että :n tapauksessa yhtälöt (6) ja (7) yksinkertaistuvat seuraavasti.
(8)
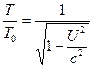(9)
Yhtälöstä (6) voidaan siis edellä esitetyn analyysin perusteella saada yksinkertainen menetelmä U:n määrittämiseksi, kunhan (φ) tunnetaan.
Viitekehykseksi valitaan yksinkertaisuuden vuoksi valonlähde, jonka liiketila vastaa havaitsijoiden liiketilaa. Havaitsija asetetaan yhdenmukaisessa lineaarisessa liikkeessä olevan suoran jäykän palkin keskelle, ja valosignaalit palkin eri kohdista saapuvat havaitsijalle eri aikoina. Havaitsija havaitsee tangon taipumisen havaitsijan paikassa taipumiskulmalla , joka saadaan yhtälöstä (8).
Tämän menetelmän avulla avaruusaluksen liiketila voitaisiin määrittää suljetusta hytistä.

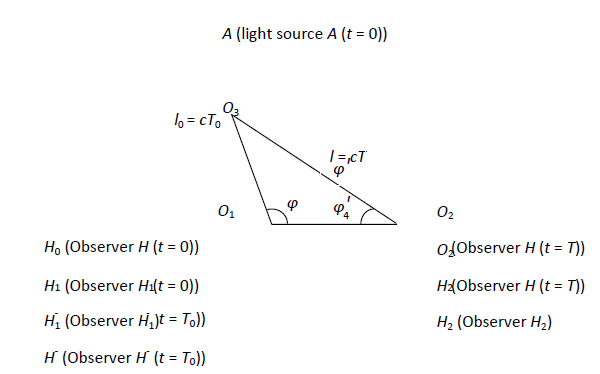
Kuva 1: havainnoitsijan ja valonlähteen liiketilat

Pituuden suhteellisuusteoria

Ylläolevassa analyysissä on otettu käyttöön kaksi pituutta, ja . Tässä tapauksessa tarkastellaan sellaisen tangon pituutta, jonka oletetaan olevan paikallaan oleva jäykkä tanko, jonka pituus L on sen koordinaatistossa, jonka L mitataan paikallaan olevalla sauvamittarilla ja jossa tangon akseli on yhteneväinen sellaisen koordinaatiston x-akselin kanssa, joka liikkuu tasaisella lineaarisella liikkeellä +x-suunnassa absoluuttisella nopeudella U. L:n oletetaan määräytyvän kahdella seuraavassa määritellyllä operaatiolla.
(a) Tarkkailija on samassa liikkuvassa koordinaatistossa kuin tanko ja sauvamittari, ja L mitataan asettamalla tanko ja sauvamittari päällekkäin.
(b) Tarkkailija mittaa useiden paikallaan oleviin koordinaatistoihin sijoitettujen kellojen avulla, jotka liikkuvat synkronoidusti, tangon molempien päiden sijainnit paikallaan olevissa koordinaatistoissa tiettynä hetkenä t, ja näiden kahden sijainnin välinen etäisyys mitataan paikallaan olevalla sauvamittarilla. on operaatiosta (a) laskettu pituus, jota kutsutaan tässä yhteydessä tangon pituudeksi liikkuvassa koordinaatistossa. on operaatiosta (b) laskettu pituus, jota tässä merkitään liikkuvan tangon pituudeksi paikallaan olevassa koordinaatistossa. On ilmeistä, että ja ovat erilaisia.
Oletetaan, että systeemissä S havaitsija H- on samassa liiketilassa kuin H. Tällöin, kuten kuvassa 1 on esitetty, H- on pisteessä O1, kun hän vastaanottaa valosignaalin kohdassa , ja samanaikaisesti havaitsija H on pisteessä O4. Näin ollen t=0,04
on H-:n ja H:n välinen etäisyys pisteessä , ja
. (10)
on etäisyys, jonka havaitsija H on kulkenut aikavälillä T0-T, niin että
. (11)
on H-:n etäisyys pisteessä ja H:n etäisyys pisteessä , siten että
. (12)
Siten voidaan johtaa seuraava lauseke:
(13)
Seuraavaksi tarkastellaan koordinaatti- ja aikamuunnoksia kahden liikkuvan koordinaatiston välillä, jotka molemmat liikkuvat tasaisella lineaarisella nopeudella, mikä edustaa uutta selitystä Lorentzin muunnokselle.
Oletetaan, että havaitsija H (systeemissä S), havaitsija H’ (systeemissä S’) ja valonlähde A” (systeemissä S”) käyttävät kaikki erikseen kalibroituja standardikelloja, ja klo valonlähde A” lähettää valosignaalin, jota nimitetään tapahtumaksi R”. Tapahtuman R” hetkellä A” on pisteessä O3, ja havaitsijat H ja H’ ovat yhtäaikaisia. Kun havaitsija H vastaanottaa valosignaalin, S-kellon lukema on T, ja H on pisteessä O1. Kun havaitsija H’ vastaanottaa valosignaalin, kellon S’ lukema on T’, ja H’ on pisteessä O2. Tällöin tapahtuman R” muunnos havaitsijoiden H’ ja H välillä voidaan laskea yhtälöstä (3), jossa
. (14)
Tässä u on havaitsijoiden H’ ja H välinen suhteellinen nopeus, jolloin saadaan seuraavat muunnokset.
(15)
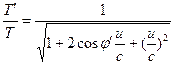(16)
:sta voidaan johtaa seuraavat suhteet:
. (17)
Kun ja , yhtälö (16) yksinkertaistuu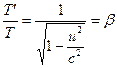
. (18)
Siten voidaan johtaa seuraavat muunnossuhteet:
, (19)
, (20)
, (21)
. (22)
Lisäksi, kun ,
, (23)
ja
, (24)
, (25)
, (26)
. (27)