De derde wet stelt dat de entropie van een stof altijd eindig is en dat deze een constante benadert naarmate de temperatuur het nulpunt nadert. De waarde van deze constante is onafhankelijk van de waarden van alle andere toestandsfuncties die de stof karakteriseren. Het staat ons vrij om voor een bepaalde stof een willekeurige waarde toe te kennen aan de nul-temperatuur grenswaarde. Wij kunnen echter niet aan alle stoffen willekeurige nultemperatuur-entropieën toekennen. De reeks van toewijzingen die we maken moet consistent zijn met de experimenteel waargenomen nul-temperatuur grenswaarden van de entropieveranderingen van reacties tussen verschillende stoffen. Voor perfect kristallijne stoffen zijn deze reactie-entropieën allemaal nul. Aan deze voorwaarde kan worden voldaan door een willekeurige waarde toe te kennen aan de molaire entropie bij nul temperatuur van elk element en te stellen dat de entropie bij nul temperatuur van een verbinding de som is van de entropieën bij nul temperatuur van de samenstellende elementen. Deze berekening wordt sterk vereenvoudigd als men de entropie bij nultemperatuur van elk element gelijk stelt aan nul. Dit is de essentiële inhoud van de derde wet.
De Lewis en Randall verklaring neemt deze keuze van de nul-temperatuur referentie toestand voor entropieën op, door deze te specificeren als “een kristallijne toestand” van elk element bij nul graden. Dientengevolge is de entropie van elke stof bij nul graden groter dan of gelijk aan nul. Dat wil zeggen, de Lewis en Randall verklaring bevat een conventie die de nul-temperatuur grenswaarde van de entropie van elke stof vastlegt. In dit opzicht maakt de Lewis en Randall verklaring een in wezen arbitraire keuze die geen intrinsieke eigenschap van de natuur is. We zien echter dat het een overweldigend handige keuze is.
We hebben alternatieve uitspraken van de eerste en tweede wet besproken. Een aantal alternatieve verklaringen van de derde wet zijn ook mogelijk. We beschouwen de volgende:
Het is onmogelijk een temperatuur van het absolute nulpunt te bereiken.
Deze uitspraak is algemener dan de Lewis en Randall uitspraak. Als we kijken naar de toepassing van deze uitspraak op de temperaturen die bereikt kunnen worden in processen met een enkele stof, dan kunnen we laten zien dat deze uitspraak de Lewis en Randall uitspraak impliceert, en erdoor geïmpliceerd wordt.
De eigenschappen van de warmtecapaciteit, ²(C_P²), spelen een centrale rol in deze argumenten. We hebben gezien dat C_P een functie is van de temperatuur. Hoewel het niet nuttig is om dit te doen, kunnen we de definiërende relatie voor \(C_P) toepassen op een stof die een faseovergang ondergaat en vinden we \(C_P=infty). Als we denken aan een stof waarvan de warmtecapaciteit kleiner is dan nul, stuiten we op een tegenstrijdigheid van onze basisideeën over warmte en temperatuur: Als q>0% en {q}/{delta T}<0%), dan moeten we \Delta T<0%) hebben; dat wil zeggen, verwarming van de stof doet de temperatuur dalen. Kortom, de theorie die we hebben ontwikkeld bevat premissen die vereisen dat voor elk systeem waaraan we metingen kunnen doen geldt:
Laat ons een zuiver systeem karakteriseren door zijn druk en temperatuur en laat ons omkeerbare constante-druk processen beschouwen waarin alleen druk-volume arbeid mogelijk is. Dan geldt: \(links(S}/rechts)}_P={C_P}/{T}}) en \(dS={C_PdT}/{T}}). We willen nu laten zien dat de Lewis en Randall bepaling dat de entropie altijd eindig is, vereist dat de warmtecapaciteit naar nul gaat als de temperatuur naar nul gaat. (Aangezien we gaan aantonen dat de derde wet metingen bij het absolute nulpunt verbiedt, is deze conclusie in overeenstemming met onze conclusie in de vorige paragraaf). Dat de warmtecapaciteit naar nul gaat als de temperatuur naar nul gaat, blijkt uit S={C_PdT}/{T}. Als S=(C_PdT) niet naar nul gaat als de temperatuur naar nul gaat, wordt S willekeurig groot als de temperatuur naar nul gaat, hetgeen in tegenspraak is met de stelling van Lewis en Randall.
Om dit resultaat explicieter uit te werken, laten we de warmtevermogens bij temperaturen \(T) en nul respectievelijk \(C_P\left(T\rechts)\) en \(C_P\left(0\rechts)\) zijn. Omdat ²(C_P\left(T\rechts)>0 voor elke ²(T>T^*>0), hebben we ²(S_P\left(T\rechts)-S\left(T^*rechts)>0 voor elke ²(T>T^*>0). Omdat de entropie altijd eindig is, is
en
Voor temperaturen in de buurt van nul, kunnen we de warmtecapaciteit, met willekeurige nauwkeurigheid, uitbreiden als een Taylorreekspolynoom in (T):
De ongelijkheden worden
De voorwaarde links stelt dat C_Pleft(0)=0.
We kunnen de derde wet zien als een uitspraak over de warmtevermogens van zuivere stoffen. We leiden niet alleen af dat C_P>0 voor alle T>0, maar ook dat
Meer algemeen kunnen we overeenkomstige beweringen afleiden voor gesloten omkeerbare systemen die geen zuivere stoffen zijn: \({links({partieel H}/{partieel T}}rechts)}_P>0}) voor alle \(T>0}), en \({\mathop{\mathrm{lim}}_{T}0} T^{-1}{links({partieel H}/{partieel T}}rechts)}_P=0}). (De entropieën bij nultemperatuur van dergelijke systemen zijn echter niet nul.) In de onderstaande discussie beschrijven we het systeem als een zuivere stof. We kunnen in essentie dezelfde argumenten gebruiken voor elk systeem; we hoeven alleen \(C_P\) te vervangen door \({links({H}/{T}}_rechts)}_P\). De Lewis en Randall stelling stelt dat de entropie naar een constante gaat bij het absolute nulpunt, ongeacht de waarden van alle andere thermodynamische functies. Hieruit volgt dat de entropie bij nul graden onafhankelijk is van de waarde van de druk. Voor twee willekeurige drukken, P_1 en P_2, geldt dat S(S)links(P_2,0rechts)-S(P_1,0rechts)=0. Stel dat ({P=P}_1) en (P_2=P+Delta P) en, dan hebben we
voor elke (\Delta P). In hoofdstuk 10 vinden we dat de entropie en het volume hun nul-temperatuur waarden asymptotisch benaderen.
Wanneer we zeggen dat het absolute nulpunt onbereikbaar is, bedoelen we dat geen enkel systeem een verandering kan ondergaan waarbij zijn eindtemperatuur nul is. Om te zien waarom het absolute nulpunt onbereikbaar moet zijn, beschouwen we processen die de temperatuur van een systeem kunnen verlagen. In het algemeen beschikken we over warmtereservoirs met verschillende temperaturen. Wij kunnen het beschikbare reservoir kiezen waarvan de temperatuur het laagst is, en het systeem op deze temperatuur brengen door eenvoudig thermisch contact. Zoveel is triviaal; de uitdaging is duidelijk om de temperatuur verder te verlagen. Om dit te doen, moeten wij een andere verandering teweegbrengen. Wat deze verandering ook moge zijn, zij kan niet worden bewerkstelligd door een uitwisseling van warmte met de omgeving. Wanneer wij het systeem eenmaal op de temperatuur van het koudste beschikbare deel van de omgeving hebben gebracht, kan elke verdere uitwisseling van warmte met de omgeving alleen maar contra-productief zijn. We concluderen dat elk proces dat geschikt is voor ons doel adiabatisch moet zijn. Omdat bij een adiabatisch proces geen warmte wordt uitgewisseld met de omgeving, moet het proces ook een mogelijk proces zijn, zodat \(\Delta S+\Delta S=0), en omdat het adiabatisch is, moet \Delta S=0). Beschouwen we een omkeerbaar proces en een onomkeerbaar proces waarin hetzelfde systeem van de toestand bepaald door P_1 en T_1 overgaat in een tweede toestand waarin de druk P_2 is. De eindtemperaturen en de entropieveranderingen van deze processen zijn verschillend. Voor het omkeerbare proces is delta S=0; de eindtemperatuur noemen we T_2. Voor het onomkeerbare proces geldt: delta S>0; de eindtemperatuur geven we aan als T^*_2. Het blijkt dat de temperatuurverandering minder is voor het onomkeerbare proces dan voor het omkeerbare proces; dat wil zeggen, \(T_2-T_1<t^*_2-t_1\)>. Equivalent, het omkeerbare proces bereikt een lagere temperatuur: \({T_2<t}^*_2\)>. Uit
kunnen we de entropie veranderingen voor deze processen berekenen. Voor het omkeerbare proces berekenen we eerst
voor de isotherme omkeerbare transformatie van toestand \(P_1), \(T_1) naar de toestand die wordt aangegeven door \(P_2) en \(T_1). Voor deze stap is \(dT\) nul, en dus
We berekenen dan
voor de isobare omkeerbare transformatie van toestand \(P_2\), \(T_1\) naar toestand \(P_2\), \(T_2\). Voor deze transformatie is dP gelijk aan nul, en is de eindtemperatuur van het systeem bepaald. We vinden \(T_2) uit
Om de entropieverandering voor het onomkeerbare proces te begrijpen, merken we eerst op dat er een oneindig aantal van zulke processen zijn. Er is niets unieks aan de eindtemperatuur. Gegeven ^(P_1), ^(T_1), en ^(P_2), kan de eindtemperatuur, ^(T^*_2), elke waarde hebben die overeenkomt met de eigenschappen van de stof. Om een bepaald onomkeerbaar proces te specificeren, moeten we alle vier de grootheden P_1, T_1, P_2 en T^*_2 specificeren. Maar nu we dat gedaan hebben, kunnen we de entropieverandering voor het onomkeerbare proces berekenen door de entropieveranderingen te berekenen als we het systeem omkeerbaar langs het isotherme tweestappenpad voeren van \naar \(P_2), \(T_1) en dan langs het isobare pad van \(P_2), \(T_1) naar \(P_2), \(T^*_2). De berekening van (\Delta S^{irrev}) voor dit omkeerbare pad van \(P_1), \(T_1) naar \(P_2), \(T^*_2) maakt gebruik van dezelfde logica als de berekening, in de vorige paragraaf, van \(\Delta S) voor het omkeerbare pad van \(P_1), \(T_1) naar \(P_2), \(T_2). Het verschil is dat T^*_2 de temperatuurintegraal vervangt door T_2 als bovengrens. De drukintegraal is hetzelfde. We hebben
Vanuit delta S^{irrev}>Delta S^{rev}), hebben we
Omdat de integranden hetzelfde zijn en positief, volgt dat ^(T^*_2>T_2), zoals hierboven beweerd.
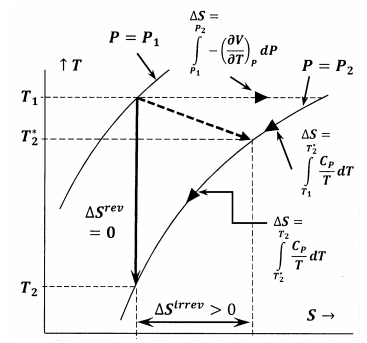
Figuur 6 toont de relaties tussen de verschillende grootheden die in dit betoog worden besproken. In het eerste geval toont figuur 6 een plot van twee van de isobaren van het systeem in de temperatuur-entropieruimte. Dat wil zeggen, de lijn met het label \(P=P_1) geeft de verzameling temperatuur-entropiepunten weer waarop het geëquilibreerde systeem de druk \(P_1) heeft; de lijn met het label \(P=P_2) geeft de evenwichtsposities weer bij druk \(P_2). Andere lijnen in deze schets stellen paden voor waarlangs het systeem omkeerbare veranderingen kan ondergaan bij constante entropie of constante temperatuur. De stippellijn stelt het onomkeerbare proces voor waarbij het systeem van de toestand bepaald door P_1, T_1 naar de toestand bepaald door P_2, T^*_2 gaat. Deze lijn is gestippeld om aan te geven dat de temperatuur van het systeem tijdens het onomkeerbare proces mogelijk niet goed gedefinieerd is.
Effectieve afkoeling kan worden bereikt met behulp van drukveranderingen als het systeem een gas is. Voor vloeistoffen en vaste stoffen geldt echter dat de temperatuurverandering bij een omkeerbare drukverandering gering is. Bij temperaturen in de buurt van het absolute nulpunt zijn bijna alle stoffen vast; om een effectieve afkoeling te bereiken moeten we een thermodynamische variabele veranderen waarvoor de temperatuurcoëfficiënt van een vast lichaam zo groot mogelijk is. Om het algemene probleem van het verlagen van de temperatuur van een systeem door het variëren van iets anders dan de druk te beschouwen, moeten we een systeem beschouwen waarin een of andere vorm van niet-druk-volumewerking mogelijk is. Een dergelijk systeem is onderhevig aan een extra kracht, en zijn energie verandert als deze kracht verandert.
Adiabatische demagnetisatie
De praktische methode waarmee extreem lage temperaturen worden bereikt, wordt adiabatische demagnetisatie genoemd. Deze methode maakt gebruik van de eigenschappen van paramagnetische vaste stoffen. In dergelijke vaste stoffen geven ongepaarde elektronen, gelokaliseerd op individuele atomen, aanleiding tot een magnetisch moment. De kwantummechanica leidt tot belangrijke conclusies over de interactie tussen dergelijke magnetische momenten en een toegepast magnetisch veld: In een toegepast magnetisch veld is het magnetisch moment van een individueel atoom gekwantiseerd. In het eenvoudigste geval kan het slechts in twee richtingen worden gericht; het moet ofwel evenwijdig aan, ofwel evenwijdig aan het toegepaste magnetische veld zijn. Wanneer het magnetisch moment van een atoom evenwijdig is aan het magnetisch veld, is de energie van het systeem lager dan wanneer de uitlijning antiparallel is. Het magneetveld oefent een kracht uit op de magnetische momenten van de afzonderlijke atomen. De energie van het systeem hangt af van de grootte van het toegepaste magnetische veld.
In plaats van ons te concentreren op het specifieke geval van adiabatische demagnetisatie, laten we de energie- en entropieveranderingen beschouwen die gepaard gaan met veranderingen in een veralgemeende potentiaal, \({\mathit{\Phi}}_{\theta } }), en zijn veralgemeende verplaatsing, \(\theta }). (Voor adiabatisch demagnetiseren zou \(\theta}) het toegepaste magnetische veld zijn). Er zijn drie variabelen nodig om omkeerbare veranderingen in dit systeem te beschrijven. We kunnen de energie en entropie uitdrukken als functies van temperatuur, druk en \theta:
(E=E-links(T,P,\theta-rechts)\) en \(S=S-links(T,P,\theta-rechts)\). Het totale differentiaal van de entropie bevat een term die de afhankelijkheid van de entropie van de \theta bepaalt. We hebben
waar we schrijven (C) links(T,P,\theta) rechts(\) om te benadrukken dat we nu voor onze huidige doeleinden de warmtecapaciteit moeten meten bij constante druk en constante \theta).
Voor constante druk, P, en constante verplaatsing, \theta), hangt de entropie af van de temperatuur als
Het postulaat dat de entropie eindig is bij elke temperatuur impliceert dat de druk- en \theta-afhankelijke warmtecapaciteit nul wordt bij het absolute nulpunt. Dat wil zeggen, bij het absolute nulpunt verdwijnt de warmtecapaciteit ongeacht de waarden van P en \theta. De redenering is precies dezelfde als voorheen. Eerder schreven we C_P links(0,P) rechts(=0); voor het huidige gegeneraliseerde geval schrijven we C links(0,P,Theta) rechts(=0).
Zo ook volgt uit het postulaat dat de entropie naar een constante bij het absolute nulpunt gaat voor alle waarden van de andere thermodynamische variabelen, dat voor elke twee drukken \(P_1) en \(P_2), en voor elke twee waarden van de gegeneraliseerde verplaatsing,
en
en dus dat
en
We willen een proces beschouwen waarin een systeem van de laagste temperatuur die in de omgeving beschikbaar is naar een nog lagere temperatuur gaat. Om de eindtemperatuur zo laag mogelijk te houden, moet dit proces adiabatisch verlopen. Het moet ook een mogelijk proces zijn, zodat de temperatuur van het systeem zo laag mogelijk is. Voor het gemak nemen we nu aan dat we dit proces uitvoeren bij een constante druk, \(P), en dat het systeem van de toestand bepaald door \(P), \(T_1), \({theta }_1) naar de toestand bepaald door \(P), \(T_2), \({theta }_2) waarbij \(T_1>T_2) gaat. De entropie van deze twee toestanden is
en 4532>
De entropieverandering voor dit proces is
Nu veronderstellen we dat de eindtemperatuur nul is; dat wil zeggen, (T_2=0), zodat
Hieruit volgt dat 4532>
waarbij de ongelijkheid aan de rechterkant volgt uit het feit dat dat 4532>(T,P,{theta }_1}rechts)>0>). Dan volgt dat
wat in tegenspraak is met de Lewis en Randall verklaring van de derde wet. De aanname dat het systeem het absolute nulpunt kan bereiken leidt tot een tegenspraak van de Lewis en Randall stelling van de derde wet. Daarom, als de Lewis en Randall stelling waar is, is het absolute nulpunt onbereikbaar.
Het omgekeerde geldt ook; dat wil zeggen, vanuit de stelling dat het absolute nulpunt onbereikbaar is, kunnen we aantonen dat de Lewis en Randall stelling waar is. Daartoe herschikken we de bovenstaande vergelijking voor \Delta S\),
Als we nu aannemen dat de Lewis en Randall stelling onwaar is, kan de uitdrukking rechts kleiner of gelijk aan nul zijn. De integraal links kan dan nul zijn, in welk geval het systeem het absolute nulpunt kan bereiken. Als de Lewis en Randall stelling vals is, is het waar dat het systeem het absolute nulpunt kan bereiken. Daarom: Als het systeem het absolute nulpunt niet kan bereiken, is de Lewis en Randall stelling waar.
Figuren 7 en 8 geven deze ideeën weer met behulp van contourplots in de temperatuur-entropie ruimte. Elke figuur toont twee contourlijnen. Een van deze contourlijnen is een stel temperatuur- en entropiewaarden waarlangs de druk constant is op P en de entropie constant is op P. De andere contourlijn is een verzameling van temperatuur- en entropiewaarden waarlangs de druk constant is op P en de entropie constant is op P2. De helling van een contourlijn is
Omdat de warmtecapaciteit altijd positief is, is deze helling ook altijd positief.
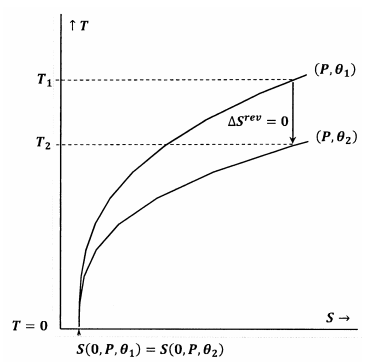
In figuur 7 wordt voldaan aan de Lewis en Randall stelling. Als de temperatuur naar nul gaat, ontmoeten de contourlijnen elkaar bij dezelfde waarde van de entropie; deze contouren voldoen aan de relatie
Een adiabatisch (verticaal) pad vanaf de contour voor \(P) en \({theta }_1) ontmoet de contour voor \(P) en \({theta }_2) bij een positieve temperatuur, \(T_2>0). Omdat dit duidelijk waar is voor elke parameter en elke parameter, zal de eindtoestand voor elk adiabatisch proces een temperatuur hebben van ⅓0. Omdat aan de Lewis en Randall stelling wordt voldaan, kan het systeem het absolute nulpunt niet bereiken, en omgekeerd.
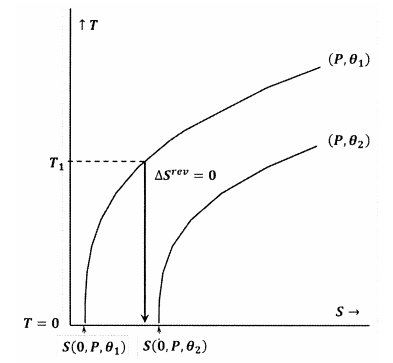
In figuur 8 wordt de Lewis en Randall stelling geschonden, omdat we \(S\left(0,P,{theta }_1)\rechts hebben.) In dit geval zal een adiabatisch proces vanuit een voldoende lage begintemperatuur, (T_1), het absolute nulpunt bereiken zonder de contour voor constante (P) en ({theta }_2) te snijden. Omdat de Lewis en Randal stelling wordt geschonden, kan het systeem het absolute nulpunt bereiken, en vice versa.