1D & 3D Convoluties uitgelegd met… MS Excel!

We begonnen met 2D Convoluties in de eerste post omdat convoluties aan populariteit wonnen na successen op het gebied van Computer Vision. Aangezien taken in dit domein gebruik maken van beelden als input, en natuurlijke beelden meestal patronen langs twee ruimtelijke dimensies (van hoogte en breedte) hebben, is het meer gebruikelijk om voorbeelden van 2D Convoluties te zien dan 1D en 3D Convoluties.

Meer recent echter, zijn er een groot aantal successen geweest in het toepassen van convoluties op natuurlijke taalverwerkingstaken ook. Aangezien de taken in dit domein tekst als input gebruiken, en de tekst patronen langs één enkele ruimtelijke dimensie (d.w.z. tijd) heeft, zijn 1D Konvoluties een uitstekende pasvorm! We kunnen ze gebruiken als efficiëntere alternatieven voor traditionele recurrente neurale netwerken (RNNs), zoals LSTMs en GRUs. In tegenstelling tot RNN’s kunnen ze parallel worden uitgevoerd voor echt snelle berekeningen.

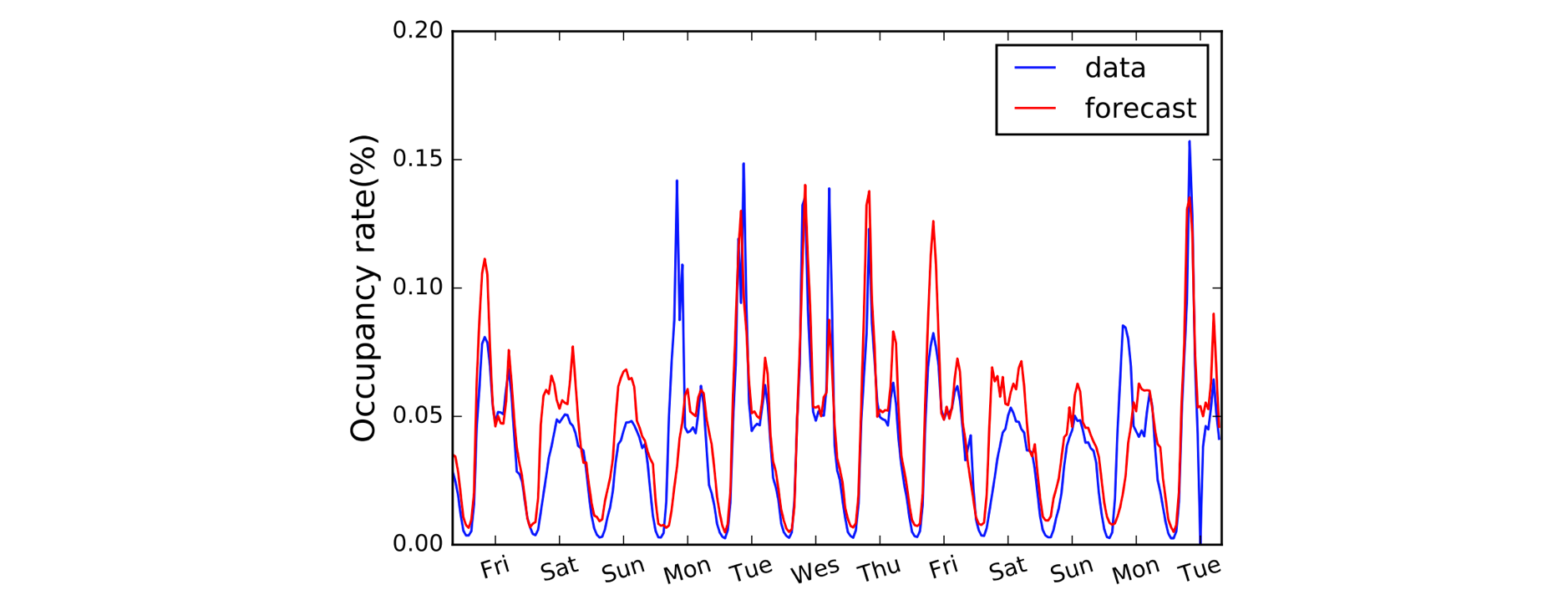
Een ander domein dat baat heeft bij 1D Convoluties is het modelleren van tijdreeksen. Zoals voorheen hebben we een enkele ruimtelijke dimensie in onze invoergegevens (d.w.z. tijd), en we willen patronen over perioden van tijd ontdekken. Wij noemen dit soort gegevens vaak “sequentieel” omdat zij kunnen worden gezien als een opeenvolging van waarden. En de ruimtelijke dimensie noemen we vaak de “temporele” dimensie. Het gebruik van 1D Convoluties voor RNN’s is ook vrij gebruikelijk: het LSTNet model is hiervan een voorbeeld en de voorspellingen ervan voor verkeersvoorspellingen zijn hieronder afgebeeld.

A, B, C. Het is eenvoudig als (1,3,3) dot (2,0,1) = 5.

Nu de naamgevingsconventies zijn opgehelderd, laten we de rekenkundige bewerkingen eens nader bekijken. We hebben geluk, want 1D Convoluties zijn eigenlijk gewoon een vereenvoudigde versie van de 2D Convolutie!

Werkend door de berekening van een enkele uitvoerwaarde, kunnen we onze kernel van grootte 3 toepassen op het gebied van gelijke grootte aan de linkerkant van onze invoerreeks. We berekenen het “dot-product” van het ingangsgebied en de kernel, wat kort samengevat gewoon het element-wise product is (d.w.z. de kleurenparen vermenigvuldigen) gevolgd door een globale som om één enkele waarde te verkrijgen. Dus in dit geval:

(1*2) + (3*0) + (3*1) = 5

We passen dezelfde bewerking (met dezelfde kernel) toe op de andere regio’s van de invoer-array om de volledige uitvoer-array van (5,6,7,2) te verkrijgen; d.w.z. we schuiven de kernel over de hele invoer-array. In tegenstelling tot 2D Convoluties, waar we de kernel in twee richtingen schuiven, schuiven we voor 1D Convoluties de kernel slechts in één enkele richting; links/rechts in dit diagram.

Geavanceerd: een 1D Convolutie is niet hetzelfde als een 1×1 2D Convolutie.

Dingen coderen

Verrassend genoeg hebben we een Conv1D Blok in Gluon nodig voor onze 1D Convolutie. We definiëren de kernelvorm als 3, en aangezien we in dit voorbeeld slechts met een enkele kernel werken, specificeren we channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

We kunnen nu onze invoer in het conv blok invoeren met behulp van een voorgedefinieerde kernel.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

Wat verandert er met padding, stride en dilation?

We zagen het effect van padding, stride en dilation in de laatste post over 2D Convoluties, en het is zeer vergelijkbaar voor 1D Convoluties. Met padding, padden we deze keer slechts langs een enkele dimensie (de temporele dimensie). Ons diagram stelt de tijd voor langs de horizontale as, dus we padden naar links en rechts van de invoergegevens (en niet boven en onder zoals in het 2D Convolutie voorbeeld). Met stride en dilation, passen we ze ook alleen toe langs de temporele dimensie. Een voorbeeld met padding en stride zou er dus als volgt uitzien:

We voegen in de code twee extra argumenten toe: padding=1 en strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Geavanceerd: de afmetingen van de invoergegevens moeten voldoen aan een bepaalde volgorde, de zogenaamde lay-out. Standaard verwacht de 1D-convolutie te worden toegepast op invoergegevens van het formaat “NCW”, d.w.z. partijgrootte (N) * kanalen (C) * breedte/tijd (W). En voor 2D Convoluties is de standaardwaarde NCHW, d.w.z. partijgrootte (N) * kanalen (C) * hoogte (H) * breedte (W). Kijk eens naar het layout argument van Conv1D en Conv2D.