3D Reconstructie

In dit practicum is het de bedoeling de nodige logica te programmeren om de kobuki-robot in staat te stellen een 3D-reconstructie te genereren van de scène die hij door zijn linker- en rechtercamera ontvangt.

Installatie

Installeer de algemene infrastructuur van de JdeRobotics Robotics Academy.

Hoe werkt uw oplossing?

Navigeer naar de 3d_reconstruction directory

cd exercises/3d_reconstruction

Lanceer Gazebo met de kobuki_3d_reconstruction wereld via het commando

roslaunch ./launch/3d_reconstruction_ros.launch

Daarna moet je de academische applicatie uitvoeren, waarin je code zal worden opgenomen:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Hoe voer je de oefening uit?

Om de oefening uit te voeren, moet u het bestand MyAlgorithm.py bewerken en daarin uw code invoegen, die 3D punten reconstrueert uit de twee stereobeelden.

Waar moet de code worden ingevoegd?

In het MyAlgorithm.py bestand,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Application Programming Interface

• self.getImage('left') – om het linker beeld
• self.getImage('right') – om het rechter beeld
• self.point.PlotPoint(position, color) – om het punt te plotten in het 3d gereedschap

Navigatie van de GUI Interface

Muis gebaseerd: Vasthouden en slepen om door de omgeving te bewegen. Scroll om in of uit te zoomen

Toetsenbord gebaseerd: Pijltjestoetsen om door de omgeving te bewegen. W en S toetsen om in of uit te zoomen

Theorie

In computer vision en computer graphics, is 3D reconstructie het proces van het bepalen van het 3D profiel van een object, alsmede het kennen van de 3D coördinaten van elk punt op het profiel. Reconstructie kan als volgt worden bereikt:

• Hardwarematig: Hardware gebaseerde benadering vereist dat we gebruik maken van de hardware die specifiek is voor de reconstructietaak. Gebruik van gestructureerd licht, laserafstandsmeter, dieptemeter en radiometrische methoden zijn enkele voorbeelden.

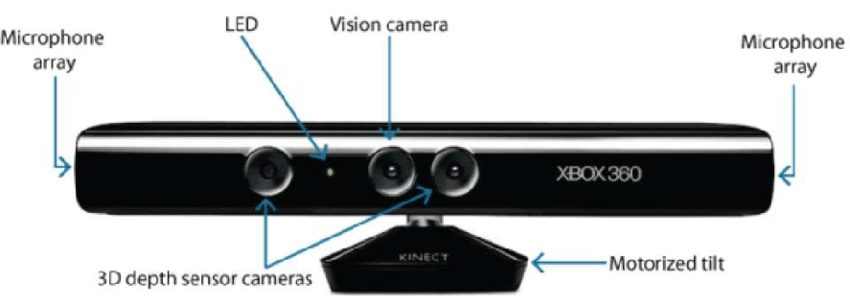
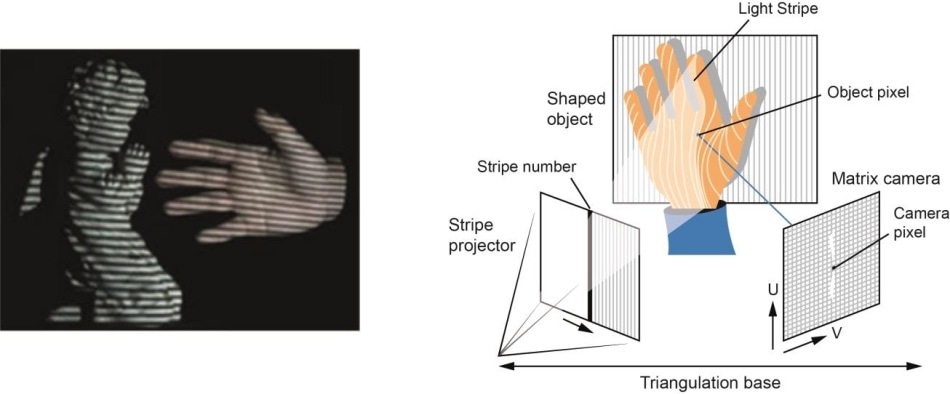
• Software Based: Software gebaseerde benadering vertrouwt op de rekencapaciteiten van de computer om de 3D eigenschappen van het object te bepalen. Vorm uit schaduw, textuur, stereo visie en homografie zijn enkele goede methoden.

In dit practicum is ons hoofddoel het uitvoeren van 3d reconstructie met behulp van Software gebaseerde benadering, in het bijzonder stereo visie 3d reconstructie.

Epipolaire Geometrie

Wanneer twee camera’s een 3D scène bekijken vanuit twee verschillende posities, zijn er een aantal geometrische relaties tussen de 3D punten en hun projecties op de 2D beelden die leiden tot constraints tussen de beeldpunten. De studie van deze eigenschappen en beperkingen wordt Epipolaire Geometrie genoemd. De onderstaande afbeelding en uitleg kunnen het idee veralgemenen:

Voorstel dat een punt X in de 3D-ruimte wordt afgebeeld in twee aanzichten, op x in het eerste en x' in het tweede. Door de stralen terug te projecteren naar hun cameracentra door de beeldvlakken, krijgen we een vlak oppervlak, aangeduid met π.

Aannemende nu dat we alleen x kennen, kunnen we ons afvragen hoe het corresponderende punt x' wordt ingeperkt. Het vlak π wordt bepaald door de basislijn (lijn die de cameracentra verbindt) en de straal gedefinieerd door x. Uit het voorgaande weten we dat de straal die correspondeert met het onbekende punt x' in π ligt, dus het punt x' ligt op de snijlijn l' van π met het tweede beeldvlak. Deze lijn wordt de epipolaire lijn genoemd die correspondeert met x. Deze relatie helpt ons om de zoekruimte van het punt in het rechter beeld, te reduceren van een vlak tot een lijn. Enkele belangrijke definities zijn:

• De epipool is het snijpunt van de lijn die de cameracentra (de basislijn) verbindt met het beeldvlak.

• Een epipolair vlak is een vlak dat de basislijn bevat.

• Een epipolaire lijn is het snijpunt van het epipolaire vlak met het beeldvlak.

Stereoreconstructie

Stereoreconstructie is een speciaal geval van de bovenstaande 3d-reconstructie waarbij de twee beeldvlakken evenwijdig aan elkaar zijn en even ver verwijderd van het 3d-punt dat we willen plotten.

In dit geval is de epipolaire lijn voor beide beeldvlakken gelijk, en zijn ze evenwijdig aan de breedte van de vlakken, wat onze constraint beter vereenvoudigt.

3D Reconstructie Algoritme

Het reconstructie algoritme bestaat uit 3 stappen:

1. Detecteer de kenmerkpunten in één beeldvlak
2. Detecteer het kenmerkpunt dat overeenkomt met het hierboven gevonden punt
3. Trianguleer het punt in 3d ruimte

Laten we ze één voor één bekijken

Detectie van kenmerkpunten

Detectie van kenmerkpunten is een uitgebreid studiegebied waar reeds verschillende algoritmen zijn bestudeerd. Harris Corner Detection en Shi-Tomasi algoritmen gebruiken eigen waarden om een goed kenmerkpunt te krijgen. Maar het probleem is dat we veel punten nodig hebben voor 3D Reconstructie, en deze algoritmen zullen niet in staat zijn om ons te voorzien van zo’n groot aantal kenmerkpunten.

Daarom gebruiken we randpunten als onze kenmerkpunten. In de volgende fase van het algoritme kan er onduidelijkheid bestaan over hun detectie. Maar ons probleem is opgelost door randen als kenmerkpunten te nemen. Een echt coole randdetector is het Canny Edge Detection Algorithm. Het algoritme is vrij eenvoudig en betrouwbaar in termen van het genereren van de randen.

Feature Point Extraction

Het gebruik van de epipolaire beperking vereenvoudigt echt de tijdscomplexiteit van ons algoritme. Voor algemene 3D reconstructie problemen, moeten we een epipolaire lijn genereren voor elk punt in een beeldframe, en dan in die sample ruimte het corresponderende punt in het andere beeldframe zoeken. Het genereren van de epipolaire lijn is in ons geval ook heel eenvoudig, het is gewoon de parallelle lijn iterpolatie van het linker beeldvlak naar het rechter beeldvlak.

Het controleren van de overeenkomst tussen beelden omvat vele algoritmen, zoals Som van Kwadraat Verschillen of Energie Minimalisatie. Zonder veel diepgang, volstaat het gebruik van een eenvoudige Correlatie filter ook voor onze use case.

Triangulatie

Triangulatie in eenvoudige termen is gewoon berekenen waar het 3d punt komt te liggen met behulp van de twee bepaalde punten in de beeldvlakken.

In werkelijkheid kan de positie van de beeldpunten niet exact gemeten worden. Voor algemene camera’s kunnen er geometrische of fysische vervormingen zijn. Er komt dus heel wat wiskunde kijken bij het minimaliseren van die fout en het berekenen van de meest nauwkeurige 3D-puntprojectie. Zie deze link voor een eenvoudig model.

Hints

Eenvoudige hints om je te helpen de 3d_reconstructie oefening op te lossen. De OpenCV bibliotheek wordt uitgebreid gebruikt voor deze oefening.

Setup

Met behulp van de oefening API, kunnen we eenvoudig de afbeeldingen ophalen. Ook is het een goed idee om, na het ophalen van de beelden, bilaterale filtering op de beelden uit te voeren, omdat er een aantal extra details zijn die niet meegenomen hoeven te worden bij de 3D reconstructie. Bekijk de illustraties voor de effecten van het uitvoeren van de bilaterale filtering.

Calculating Correspondences

OpenCV heeft al ingebouwde correlatie filters die kunnen worden aangeroepen via matchTemplate(). Let op extreme gevallen zoals randen en hoeken.

Een goede observatie is dat de punten aan de linkerkant correspondentie zullen hebben in het linker gedeelte en de punten aan de rechterkant correspondentie zullen hebben in het rechter gedeelte. Met behulp van deze observatie kunnen we gemakkelijk de berekening van de correspondentie versnellen.

Plotten van de punten

Handmatig of OpenCV-gebaseerde functie triangulatePoints werkt goed voor driehoeksmeting. Let gewoon op alle matrixvormen en -groottes bij het uitvoeren van de algebraïsche implementaties.

Houd het verschil in gedachten tussen eenvoudige 3D coördinaten en homogene 4D coördinaten. Bekijk deze video voor details. Simpelweg de volledige 4d vector delen door zijn 4e coördinaat geeft ons de 3d coördinaten.

Door verschillende implementaties van gebruikers, kan het zijn dat de gebruiker de schaal en offset van de driehoekspunten moet aanpassen om ze zichtbaar en representeerbaar te maken in de GUI interface. Downscaling van de 3D coördinatenvector met een waarde tussen 500 en 1000 werkt goed. Ook een offset van 0 tot 8 werkt goed.

Illustraties