Abeliaanse groep | CDhistory

Een Abeliaanse groep is een groep waarvan de elementen commuteren (d.w.z. voor alle elementen en ). Abelische groepen komen dus overeen met groepen met symmetrische tafels van vermenigvuldiging.

Alle cyclische groepen zijn Abelisch, maar een Abelische groep is niet noodzakelijk cyclisch. Alle ondergroepen van een Abeliaanse groep zijn normaal. In een Abeliaanse groep bevindt elk element zich in een eigen conjugatieklasse, en de karaktertabel omvat machten van een enkel element, bekend als een groepsgenerator.

In de Wolfram-taal vertegenwoordigt de functie AbelianGroup het directe product van de cyclische groepen van graden , , ….

Er is geen algemene formule bekend voor het geven van het aantal niet-isomorfe eindige groepen van een gegeven groepsorde. Het aantal niet-isomorfe Abelische eindige groepen van een gegeven groepsorde wordt echter gegeven door te schrijven als

(1)

waar de verschillende priemfactoren zijn, dan

(2)

waar de verdelingsfunctie is, die in de Wolfram Language is geïmplementeerd als FiniteAbelianGroupCount. De waarden van voor , 2, … zijn 1, 1, 1, 2, 1, 1, 1, 3, 2, … (OEIS A000688).

De kleinste ordes waarvoor , 2, 3, … niet-isomorfe Abeliaanse groepen bestaan zijn 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), waarbij 0 staat voor een onmogelijk aantal (d.w.z. geen product van partitiegetallen) van niet-isomorfe Abeliaanse groepen. De “ontbrekende” waarden zijn 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). De incrementeel grootste getallen van Abeliaanse groepen als functie van de orde zijn 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), die voorkomen voor de orden 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

De Kronecker decompositietheorema stelt dat elke eindige Abeliaanse groep kan worden geschreven als een groepsdirect product van cyclische groepen van priemmachtige groepsorde. Als de groepsorde van een eindige groep een priem is, dan bestaat er een enkele Abeliaanse groep van orde (aangeduid met ) en geen niet-Abeliaanse groepen. Als de groepsorde een kwadratisch priemgetal is, dan zijn er twee Abeliaanse groepen (aangeduid met en . Is de groepsorde een priemgetal , dan zijn er drie Abeliaanse groepen (aangeduid met , , en ), en vijf groepen in totaal. Als de orde een product is van twee priemgetallen en , dan bestaat er precies één Abeliaanse groep van groepsorde (aangeduid met ).

Een ander interessant resultaat is dat als het aantal niet-isomorfe Abeliaanse groepen van groepsorde aanduidt, dan

(3)

waar de Riemann zeta-functie is.

De getallen van Abeliaanse groepen van de orden zijn gegeven door 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) voor , 2, …. Srinivasan (1973) heeft ook aangetoond dat

(4)

waar

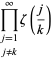			(5)
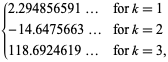			(6)

(OEIS A021002, A084892, en A084893) en is weer de Riemann zeta functie. Merk op dat Richert (1952) ten onrechte gaf. De sommen kunnen ook geschreven worden in de expliciete vormen