Abstract
Licht verplaatst zich door een vacuüm met snelheid c ongeacht de beweging van de lichtbron of die van het referentiekader van een waarnemer. Bijgevolg is er enige tijd nodig voor licht om van een lichtbron naar een waarnemer in de ruimte te reizen, zodat de emissie van licht en de waarneming van het uitgezonden licht niet gelijktijdig zijn. Op basis van deze overwegingen wordt een methode voorgesteld om de absolute snelheid van een waarnemer te meten, die zou kunnen worden gebruikt om de bewegingstoestand van een ruimteschip vanuit een gesloten cabine te bepalen. In deze studie wordt ook een nieuwe verklaring van de Lorentz-transformatie geïntroduceerd.
Key words
coördinatenstelsel, referentiestelsel, beweging, absolute snelheid, relativiteit, Lorentz-transformatie, tijd, ruimte, waarnemer, lichtbron
De volgende analyse presenteert een praktische benadering voor het meten van de absolute snelheid van een waarnemer, die gebruikt zou kunnen worden voor het bepalen van de bewegingstoestand van een ruimteschip vanuit een gesloten cabine. Het begrip absolute snelheid verwijst in het algemeen naar een standaard uniforme snelheid van de verschillende objecten van een fysisch systeem ten opzichte van een gepostuleerde onbeweeglijke ruimte die onafhankelijk bestaat van de fysische objecten die er deel van uitmaken (d.w.z. een absolute ruimte). In dit artikel presenteren wij een benadering op basis van starre kinematica om aan te tonen dat de absolute snelheid van een waarnemer kan worden bepaald uit het feit dat licht met snelheid c door een vacuüm reist, ongeacht de beweging van de lichtbron of die van het referentiekader van een waarnemer. Bijgevolg is er enige tijd nodig voor licht om van een lichtbron naar een waarnemer in de ruimte te reizen, zodat de emissie van licht en de waarneming van het uitgezonden licht niet gelijktijdig zijn.
In de voorgestelde analyse geven wij eerst de volgende conventies voor de beschouwde coördinatenstelsels. Wij gaan uit van een Cartesisch coördinatenstelsel bestaande uit drie paarsgewijs loodrecht op elkaar staande assen, uitgaande van het punt (0,0,0), waarbij elk punt P in de ruimte kan worden gedefinieerd door zijn coördinaten langs de x-, y- en z-as, voorgesteld door een geordend paar reële getallen (x,y,z). Een traagheidsreferentiestelsel S wordt verondersteld te worden weergegeven door een rechthoekig ruimtecoördinatenstelsel (x,y,z) waarvan de oorsprong O is. Een reeks standaardklokken (aangeduid als S-klokken) bevindt zich op stationaire punten in S. De S-klokken zijn onderling gekalibreerd (d.w.z. zij geven gelijkwaardige waarden op hetzelfde tijdstip) op basis van de transmissie en ontvangst van een lichtsignaal. Meer bepaald wordt op tijdstip tA een lichtstraal van klok A op klok B geprojecteerd, die vervolgens op tijdstip tB door klok B wordt teruggekaatst in de richting van klok A, en op tijdstip tA’ bij klok A aankomt. Als 
, zijn de twee klokken gekalibreerd. Voor elke gebeurtenis die zich op coördinaten x,y,z bevindt, wordt zijn tijdcoördinaat t gegeven door de aflezing van de gebeurtenisgerelateerde S-klok. Op soortgelijke wijze wordt een ander traagheidsreferentiestelsel S’ vastgesteld op basis van een tweede rechthoekig ruimtecoördinatenstelsel (x’,y’,z’) waarvan de oorsprong O’ is, en wordt een andere reeks wederzijds geijkte standaardklokken (S’-klokken) geplaatst op stationaire punten in referentiestelsel S’.
Omdat de respectieve oorsprong van de ruimtelijke en temporele coördinaten, alsmede de richtingen van de coördinatenassen in hoge mate willekeurig kunnen worden gekozen, zijn de hier gebruikte relaties tussen S en S’ gebaseerd op de volgende conventies, die ter vereenvoudiging zijn toegepast.
(1) Op een bepaald tijdstip worden de oorsprong en de coördinatenassen van de twee stelsels boven elkaar geplaatst, en worden de klokken respectievelijk in O en O’ op nul gezet, d.w.z, 
(2) De x- en x’-assen vallen samen in de richting van de relatieve beweging van S en S’; dus x en x’ vallen op elk moment samen, terwijl y en y’, evenals z en z’ evenwijdig zijn.
(3) S’ beweegt langs de +x-richting van S.
De voorgestelde analyse is gebaseerd op het fundamentele principe dat licht in vacuüm met een constante snelheid c beweegt, ongeacht de beweging van de waarnemer of de lichtbron. Daarom definiëren wij hierin de absolute snelheid U van de waarnemer, die wordt verondersteld lineair en uniform te zijn, als 
, waarbij f(φ) een functie is van de geometrische relatie tussen de richting van een lichtsignaal en de richting van U, hierin aangeduid als φ.
Twee nieuwe verklaringen van de relativiteit van tijd en lengte worden gegeven in de voorgestelde analyse, die verschillen van Einsteins verklaringen (zie “Over de elektrodynamica van bewegende lichamen”). Deze verklaringen worden in de volgende secties geïntroduceerd.
De relativiteit van de tijd
Op grond van de eindige snelheid van het licht is er enige tijd nodig voor het licht om van een lichtbron naar een waarnemer in de ruimte te reizen. Hieruit kan worden afgeleid dat de emissie van licht en de waarneming van licht niet gelijktijdig kunnen plaatsvinden. Uitgaande van de constantheid van de lichtsnelheid en de in figuur 1 geïllustreerde voorwaarden, definiëren wij de volgende factoren. De posities van een lichtbron en een waarnemer op 
, op welk moment de lichtbron licht uitstraalt (aangeduid als gebeurtenis R), worden respectievelijk gegeven als A en H0. Tijdens de voortplantingsperiode van het licht van 
tot 
legt de waarnemer een afstand U∙T af van positie H0 tot H, waarna de waarnemer het uitgezonden licht ontvangt. Dienovereenkomstig definiëren wij 
als de afstand l tussen de positie van de waarnemer bij ontvangst van het lichtsignaal op 
en de positie van de lichtbron bij het uitzenden van licht op 
. Door de constantheid van de lichtsnelheid is 
. De afstand 
is gelijk aan U∙T. Tenslotte definiëren we 
als de afstand l0 tussen de positie van de waarnemer op 
en de positie van de lichtbron op 
. Hier introduceren wij een beschouwing van de positie van de waarnemer op 
, waarvan eerder werd gedacht dat zij geen fysische betekenis had. Als de bewegingstoestanden van de waarnemer en de lichtbron gelijkwaardig zijn, is l0 gegeven, zodat U kan worden berekend via de driehoeksrelaties die zijn afgebeeld in figuur 1.
In het huidige werk wordt de tijd van een gebeurtenis gemeten volgens de volgende methode. Zowel de waarnemer als een klok worden op de oorsprong geplaatst. Wanneer het lichtsignaal dat de gebeurtenis vertegenwoordigt de waarnemer bereikt, zal de aankomsttijd van het licht overeenkomen met de door de klok aangegeven tijd. Het voordeel van deze overeenkomst is dat zij altijd gerelateerd is aan de positie van de waarnemer die de klok hanteert. Zoals te zien is in figuur 1, kan ruimtelijk punt O3 worden gedefinieerd op basis van de positie van de lichtbron wanneer deze licht uitstraalt op 
, en kan ruimtelijk punt O2 worden gedefinieerd op basis van de positie van de waarnemer wanneer deze licht ontvangt op 
. De manier om het ruimtelijke punt O1 te definiëren waar de waarnemer zich bevindt wanneer de lichtbron licht uitstraalt op 
ligt echter niet voor de hand. Om dit probleem op te lossen, worden de begrippen absolute rust (d.w.z. 
) en absolute beweging (d.w.z. 
) geïntroduceerd. We vervangen respectievelijk de enkele bewegende waarnemer op H0 en H door twee waarnemers H1 en H2 in rust op ruimtelijke punten O1 en O2, terwijl lichtbron A in rust is op ruimtelijk punt O3. Elk van de waarnemers en de lichtbron gebruiken geijkte standaardklokken, en A zendt een lichtsignaal uit op 
, aangeduid als gebeurtenis R0. Wanneer waarnemer H1 het lichtsignaal met een snelheid van c ontvangt, is de meting van de klok T0, en wanneer H2 het lichtsignaal ontvangt, is de meting T. De afstanden 
en 
kunnen dus als volgt worden gedefinieerd op basis van de respectieve reistijden van het lichtsignaal:
, (1)
en
. (2)
Volgens de driehoeksrelaties in figuur 1 is de transformatie van gebeurtenis R0 tussen de waarnemers H1 en H2 als volgt.
(3) 
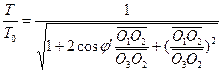(4)
Hierbij is 
de hoek tussen de lijn O3O1 en de x-as, en 
de hoek tussen de lijn O3O2 en de x-as.
Terugkomend op de toestand van een enkele bewegende waarnemer, nemen we aan dat in systeem S zowel de waarnemer H als lichtbron A een geijkte standaardklok gebruiken. Op het moment van de gebeurtenis R bevindt lichtbron A zich in ruimtelijk punt O3, en waarnemer H in ruimtelijk punt O1. Het tijdstip waarop het lichtsignaal ruimtelijk punt O1 bereikt, komt overeen met een S-klokaflezing van T0. Wanneer waarnemer H het lichtsignaal ontvangt, is de aflezing T, en bevindt H zich op O2.
Hij kan gebeurtenis R in punt O1 natuurlijk niet waarnemen. Om dit probleem op te lossen, wordt een andere waarnemer H- in systeem S geplaatst in het punt O1 dat overeenkomt met 
, waarbij de positie van H- wordt gebruikt om ruimtelijk punt O1 te definiëren. De transformatie van gebeurtenis R tussen waarnemers H- en H kan dan als volgt worden verkregen met behulp van vergelijking (3). 
(5)
Hieruit volgt dat vergelijkingen (3) en (4) als volgt kunnen worden herschreven.
(6) 
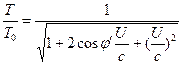(7)
e zien ook dat, voor 
, vergelijkingen (6) en (7) tot het volgende worden vereenvoudigd.
(8) 
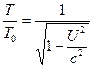(9)
Op basis van bovenstaande analyse kan dus uit vergelijking (6) een eenvoudige methode worden verkregen om U te bepalen, gegeven dat 
(φ) bekend is.
Voor de eenvoud wordt een lichtbron met een gelijkwaardige bewegingstoestand als die van de waarnemers als referentiekader gekozen. Een waarnemer wordt geplaatst in het midden van een rechte stijve staaf in uniforme lineaire beweging, en lichtsignalen van verschillende posities op de staaf komen op verschillende tijdstippen bij de waarnemer aan. De waarnemer detecteert de afbuiging van de staaf op de positie van de waarnemer met een afbuighoek 
die kan worden verkregen uit vergelijking (8).
Met deze methode zou de bewegingstoestand van een ruimtevaartuig vanuit een gesloten cabine kunnen worden bepaald.
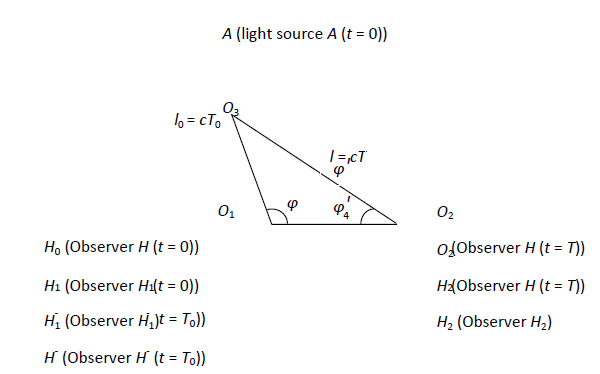
Figuur 1: bewegingstoestanden van de waarnemer en de lichtbron
De relativiteit van lengte
In de bovenstaande analyse zijn twee lengtes geïntroduceerd, te weten 
en 
. In dit geval beschouwen we de lengte van een staaf die wordt verondersteld een stationaire stijve staaf te zijn met lengte L binnen zijn coördinatensysteem, waarvoor L wordt gemeten met een stationaire stafmaat, en waarbij de as van de staaf samenvalt met de x-as van een coördinatensysteem dat met eenparige lineaire beweging langs de +x-richting beweegt met een absolute snelheid U. Er wordt verondersteld dat L wordt bepaald door de twee hieronder gedefinieerde operaties.
(a) De waarnemer bevindt zich in hetzelfde bewegende coördinatenstelsel als de staaf en de baakmeter, en L wordt gemeten door de staaf en de baakmeter op elkaar te leggen.
(b) Met behulp van verschillende klokken die in stationaire coördinaten zijn geplaatst en die synchroon bewegen, meet de waarnemer de posities van de twee uiteinden van de staaf in stationaire coördinaten op een bepaald moment t, en de afstand tussen de twee posities wordt gemeten met de stationaire baakmeter. 
is de lengte berekend uit bewerking (a), die hier wordt aangeduid als de staaflengte in de bewegende coördinaat. 
is de lengte berekend uit bewerking (b), die hierin wordt aangeduid als de lengte van een bewegende staaf in de stationaire coördinaat. Het is duidelijk dat 
en 
verschillend zijn.
We nemen aan dat, in systeem S, waarnemer H- zich in dezelfde bewegingstoestand bevindt als H. Dan, zoals weergegeven in figuur 1, bevindt H- zich in punt O1 wanneer hij het lichtsignaal ontvangt op 
, en, tegelijkertijd, bevindt waarnemer H zich in punt O4. Daarom is t=0,04
de afstand tussen H- en H op 
, en 
. (10)
is de afstand afgelegd door waarnemer H in het interval van T0 tot T, zodanig dat
. (11)
is de afstand tussen H- bij 
en H bij 
, zo dat
. (12)
Hieruit kan de volgende uitdrukking worden afgeleid.
(13)
Volgende beschouwen we de coördinaten- en tijdstransformaties tussen twee bewegende coördinatenstelsels, die beide met een uniforme lineaire snelheid bewegen, wat een nieuwe uitleg van de Lorentztransformatie vormt.
Aannemende dat waarnemer H (in systeem S), waarnemer H’ (in systeem S’), en lichtbron A” (in systeem S”) alle afzonderlijk geijkte standaardklokken gebruiken, en op 
zendt lichtbron A” een lichtsignaal uit, aangeduid als gebeurtenis R”. Op het moment van de gebeurtenis R” bevindt A” zich in punt O3, en vallen de waarnemers H en H’ samen. Wanneer waarnemer H het lichtsignaal ontvangt, is de aflezing van de S-klok T, en bevindt H zich in punt O1. Wanneer waarnemer H’ het lichtsignaal ontvangt, is de aflezing van de klok van S’ T’, en H’ bevindt zich in punt O2. Dan kan de transformatie van gebeurtenis R” tussen de waarnemers H’ en H’ worden berekend uit vergelijking (3), waarin
. (14)
Hierbij is u de relatieve snelheid tussen de waarnemers H’ en H, hetgeen de volgende transformaties oplevert. 
(15) 
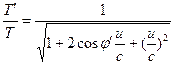(16)
Uit 
kunnen de volgende relaties worden afgeleid: 
. (17)
Wanneer 
en 
, vereenvoudigt vergelijking (16) tot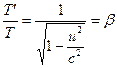
. (18)
Daaruit kunnen de volgende transformatierelaties worden afgeleid:
, (19)
, (20)
, (21)
. (22)
Meer, wanneer 
, 
, (23)
en 
, (24)
, (25)
, (26)
. (27)