Berekening van het gemiddelde jaarlijkse verlies
Stel dat u de AAL wilt berekenen voor een geografisch gespreide portefeuille van eigendommen met behulp van een 10-jarige orkaancatalogus (let op: dit is een gekunsteld voorbeeld ter illustratie; werkelijke catalogi bevatten doorgaans 10.000, 50.000 of zelfs 100.000 jaar van gesimuleerde activiteit). In elk gesimuleerd jaar kunnen er nul, één of meerdere orkanen zijn die de portefeuille beïnvloeden. Het uitvoeren van het model tegen deze portefeuille in AIR software levert de verliezen op die worden getoond in Tabel 1.
| Hurricane | |
|---|---|
| Simulatiejaar | Verlies (miljoenen USD) |
| 1 | 25 |
| 2 | 0 |
| 3 | 17 |
| 4 | 34 |
| 5 | 99 |
| 6 | 67 |
| 7 | 0 |
| 8 | 31 |
| 9 | 55 |
| 10 | 29 |
Deze verliezen worden vervolgens gerangschikt om tot een overschrijdingskanscurve te komen en ook gemiddeld om de geaggregeerde AAL te berekenen, zoals weergegeven in figuur 1. In dit voorbeeld bedraagt de AAL 36 miljoen USD. Merk op dat zeven jaren lagere verliezen veroorzaken dan de AAL en dat drie jaren hogere verliezen veroorzaken. In twee jaar werd de portefeuille niet door orkanen getroffen en waren de verliezen nul.
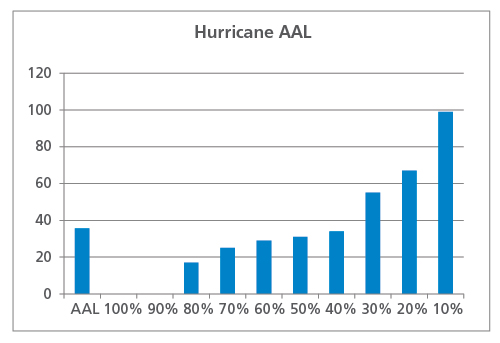
Wat AAL niet onthult
Stel dat dezelfde hypothetische vastgoedportefeuille zich in de buurt van een aardbevingsbreuk bevindt waarvan wordt verwacht dat hij eens in de vijf jaar zal scheuren. Het doorlopen van een 10-jarige aardbevingscatalogus met de portefeuille zou de verliezen kunnen opleveren die in Tabel 2 worden getoond. Hypothetische 10-jaarcatalogus van aardbevingen
De EP-curve en AAL kunnen worden berekend zoals eerder, zoals getoond in figuur 2. De AAL voor aardbevingen lijkt sterk op die voor orkanen, namelijk 40 miljoen USD, maar het is onmiddellijk duidelijk dat het risicoprofiel van deze twee gevaren zeer verschillend is.
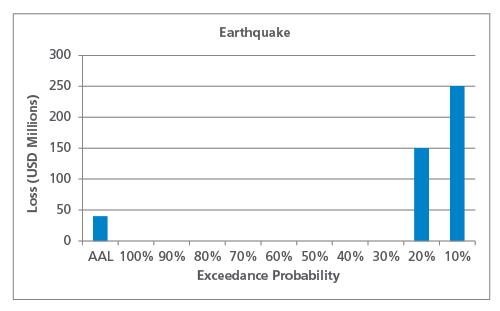
Zoals uit dit vereenvoudigde voorbeeld blijkt, zal voor gevaren die worden gekenmerkt door weinig voorkomende schadeveroorzakende gebeurtenissen (zoals aardbevingen), de staart van de verdeling met een lage frequentie en een grote impact meer bijdragen aan de AAL dan gevaren die een hogere frequentie van minder schadeveroorzakende gebeurtenissen vertonen. Dit is belangrijk om in gedachten te houden bij het vergelijken van de historische AAL (berekend op basis van een beperkt aantal jaren) met de gemodelleerde AAL. Voor risico’s waarvan de AAL wordt bepaald door de staart van de verdeling, zal de historische AAL waarschijnlijk veel lager zijn dan de gemodelleerde als een grote gebeurtenis zich niet heeft voorgedaan binnen de tijdspanne van de geregistreerde gegevens.
Geaggregeerde en occurrence AAL
Zoals eerder vermeld, kan AAL worden bepaald op een geaggregeerde of occurrence basis. Net als in de natuur kan elk jaar nul, één of meer schadeveroorzakende gebeurtenissen hebben, en geaggregeerde AAL houdt rekening met alle verliesveroorzakende gebeurtenissen in elk gesimuleerd jaar. Verliezen van alle gebeurtenissen worden opgeteld en vervolgens gedeeld door het aantal jaren in de catalogus, zoals getoond in de voorbeelden in de vorige sectie.
Occurrence AAL, aan de andere kant, is alleen gebaseerd op het grootste verlies in elk gesimuleerd jaar, dus als twee identieke verliezen in hetzelfde jaar optreden, draagt slechts een bij aan de occurrence AAL. In het volgende voorbeeld wordt de berekening conceptueel toegelicht. Merk echter op dat de AAL van een voorval geen erg zinvol beeld van het risico geeft; het gebruik van de geaggregeerde AAL wordt aanbevolen.
Tabel 3 toont dezelfde 10-jarige orkaancatalogus, maar deze keer uitgesplitst per gebeurtenis. Het grootste verlies van elk jaar is gemarkeerd.
Tabel 3. Hypothetische 10-jarige orkaancatalogus, uitgesplitst per gebeurtenis
| Hurricane | ||
|---|---|---|
| Simulatiejaar | Event Number | Verlies (miljoenen USD) |
| 1 | 1 | 25 |
| 2 | 0 | |
| 3 | 2 | 13 |
| 3 | 4 | |
| 4 | 4 | 27 |
| 5 | 7 | |
| 5 | 6 | 16 |
| 7 | 2 | |
| 8 | 49 | |
| 9 | 32 | |
| 6 | 10 | 43 |
| 11 | 11 | |
| 12 | 13 | |
| 7 | 0 | |
| 8 | 13 | 31 |
| 9 | 14 | 55 |
| 10 | 15 | 7 |
| 16 | 22 | |
Uitsluitend rekening houdend met het grootste verlies van elk jaar, De EP-curve en de AAL-voorvalcurve zijn weergegeven in figuur 3.
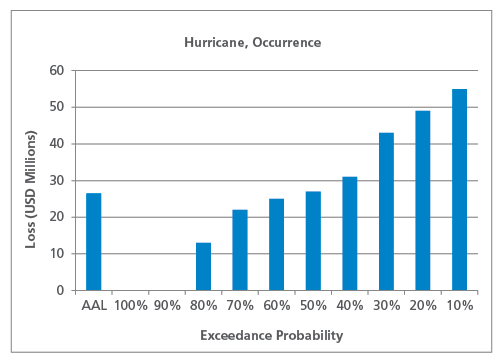
Zoals verwacht is de occurrence AAL (26,5 miljoen USD) lager dan de aggregate AAL. Ook hier is de aard van de gebeurtenis van invloed op de vorm van de EP-curve en de verhouding tussen AAL van de gebeurtenis en AAL van het aggregaat. Bij laagfrequente risico’s zoals aardbevingen is het bijvoorbeeld minder waarschijnlijk dat zich in hetzelfde jaar meerdere schadeveroorzakende gebeurtenissen voordoen, zodat het AAL van een gebeurtenis dichter bij het totale AAL zal liggen dan bij hoogfrequente risico’s zoals zware onweersbuien.
Dichtende gedachten
Hoewel de voorbeelden in dit artikel sterk vereenvoudigd zijn voor illustratieve doeleinden, is het basispunt dat terwijl de AAL slechts één getal is en altijd op dezelfde manier wordt berekend, de verdeling erachter er heel verschillend kan uitzien, afhankelijk van gevaar, regio en andere gevaren- en kwetsbaarheidskenmerken. In een volgend artikel zullen we dieper ingaan op het concept van de EP-curvevormen en de invloed ervan op de AAL, en zullen we ook enkele veelgestelde vragen en misvattingen over de AAL bespreken.