Tolerantie-intervallen
Dit gedeelte bevat statistische details voor eenzijdige en tweezijdige tolerantie-intervallen.
Normale verdelingsgebaseerde intervallen
Eenzijdig interval
Het eenzijdige interval wordt als volgt berekend:
Ondergrens = 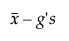
Bovengrens = 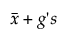
waar
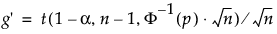
s is de standaardafwijking
t is het kwantiel uit de niet-centrale t-verdeling
Φ-1 is het standaardnormale kwantiel
Tweezijdig interval
Het tweezijdige interval wordt als volgt berekend:
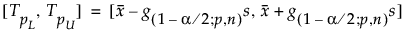
waarbij s de standaardafwijking is en g(1-α/2; p,n) een constante.
Om g te bepalen moet worden gekeken naar de fractie van de populatie die door het tolerantie-interval wordt bestreken. Tamhane en Dunlop (2000) geven deze fractie als volgt weer:
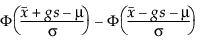
waarbij Φ staat voor de standaardnormale cdf (cumulatieve verdelingsfunctie).
Daaruit lost g de volgende vergelijking op:
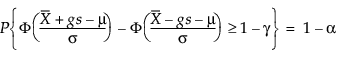
waarbij 1 – γ de fractie is van alle toekomstige waarnemingen die in het tolerantie-interval liggen.
Voor meer informatie over op de normale verdeling gebaseerde tolerantie-intervallen, zie de tabellen J.1a, J.1b, J.6a, en J.6b van Meeker et al. (2017).
Nonparametrische intervallen
Eenzijdige ondergrens
De lagere 100(1 – α)% eenzijdige tolerantiegrens om ten minste een deel β van de bemonsterde verdeling uit een steekproef van grootte n te bevatten, is de orderstatistiek x(l). De index l wordt als volgt berekend:
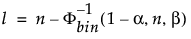
waarbij Φ-1bin(1-α, n, β) het (1 – α)e kwantiel is van de binomiale verdeling met n proeven en kans op succes β.
Het werkelijke betrouwbaarheidsniveau wordt berekend als Φbin(n-l, n, β), waarbij Φbin(x, n, β) de kans is dat een binomiaal verdeelde willekeurige variabele met n proeven en kans op succes β kleiner is dan of gelijk is aan x.
Merk op dat om een lager eenzijdig verdelingsvrij tolerantie-interval te berekenen, de steekproefgrootte n ten minste zo groot moet zijn als 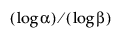 .
.
Eenzijdige bovengrens
De bovenste 100(1 – α)% eenzijdige tolerantiegrens om ten minste een deel β van de bemonsterde verdeling uit een steekproef van grootte n te bevatten, is de orderstatistiek x(u). De index u wordt als volgt berekend:
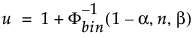
waarbij Φ-1bin(1-α, n, β) het (1 – α)e kwantiel is van de binomiale verdeling met n proeven en kans op succes β.
Het werkelijke betrouwbaarheidsniveau wordt berekend als Φbin(u-1, n, β), waarbij Φbin(x, n, β) de kans is dat een binomiaal verdeelde willekeurige variabele met n proeven en kans op succes β kleiner is dan of gelijk aan x.
Merk op dat voor het berekenen van een tolerantie-interval zonder eenzijdige bovenverdeling de steekproefgrootte n ten minste zo groot moet zijn als 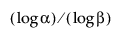 .
.
Tweezijdig interval
Het tweezijdige tolerantie-interval van 100(1 – α)% dat ten minste een deel β van de bemonsterde verdeling uit een steekproef van grootte n moet bevatten, wordt als volgt berekend:
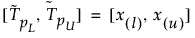
waarbij x(i) de ide ordestatistiek is en l en u als volgt worden berekend:
Let ν = n – Φ-1bin(1-α, n, β), waarbij Φ-1bin(1-α, n, β) het (1 – α)e kwantiel is van de binomiale verdeling met n proeven en kans op succes β. Indien ν kleiner is dan 2, kan geen tweezijdig verdelingsvrij tolerantie-interval worden berekend. Als ν groter dan of gelijk aan 2 is, geldt l = floor(ν/2) en u = floor(n + 1 – ν/2).
Het werkelijke betrouwbaarheidsniveau wordt berekend als Φbin(u-l-1, n, β), waarbij Φbin(x, n, β) de kans is dat een binomiaal verdeelde willekeurige variabele met n proeven en kans op succes β kleiner is dan of gelijk is aan x.
Merk op dat om een tweezijdig verdelingsvrij tolerantie-interval te berekenen, de steekproefgrootte n ten minste even groot moet zijn als de n in de volgende vergelijking:

Voor meer informatie over verdelingsvrije tolerantie-intervallen, zie Meeker et al. (2017, sec. 5.3).