De aftrekkingsprocedure voor PL-eliminatie werd zo’n twee decennia geleden voor het eerst uitgewerkt. Deze procedure heeft geen invloed op de ECG-componenten die grenzen aan de PL-frequentie. Deze theoretische studie is uitgevoerd voor de basis-FL-frequentie, maar de conclusies gelden ook voor de harmonischen ervan en dus voor een willekeurige interferentiegolfvorm. De efficiëntie van de procedure is niet afhankelijk van de amplitude van de interferentie, zolang de versterker niet verzadigd is. Bovendien kan de procedure goed omgaan met veranderingen in amplitude en frequentie van de interferentie. De procedure is in de loop der jaren voortdurend verbeterd en in duizenden ECG-instrumenten en computerondersteunde systemen geïmplementeerd. Vergelijkbare benaderingen zijn ook door andere onderzoekers gepubliceerd.
- Principes
- Lineair criterium
- Compensatie van PL-amplitudevariaties
- Lineaire filtering
- Compensatie van variatie in PL-frequentie
- Efficiëntiebeoordeling van de procedure
- Invloed van EMG-ruis
- Storingsonderdrukking in hoge-resolutie ECG
- Geval van apparaten op batterijen en computerondersteunde ECG-systemen
- Automatische aanpassing aan de nominale PL-frequentie
- Ontwikkeling van de theoretische procedure
Principes
De aftrekkingsprocedure wordt oorspronkelijk toegepast met bemonsteringsfrequentie f S , een veelvoud van, en hardware gesynchroniseerd met de PL-frequentie f PL . De procedure bestaat uit de volgende stappen:
-
ECG-segmenten met frequentieband dichtbij nul worden continu gedetecteerd met behulp van een geschikt criterium. Zij worden lineaire segmenten genoemd en worden hoofdzakelijk aangetroffen in de PQ- en TP-intervallen, maar ook in voldoende lange rechte delen van de R- en T-golven.
-
De monsters van deze segmenten worden bewegend gemiddeld, d.w.z. onderworpen aan een lineair fasekamfilter met een eerste nul op f PL . De gefilterde monsters bevatten dus geen interferentie.
-
Interferentie-amplituden, correcties genoemd, worden berekend voor elk van de in fase vergrendelde monsters, n, in de PL-periode, T PL , door de gefilterde monsters af te trekken van de overeenkomstige monsters van het gecontamineerde (oorspronkelijke) ECG-signaal.
-
De verkregen set correcties wordt voortdurend bijgewerkt in lineaire segmenten en gebruikt in niet-lineaire segmenten (gewoonlijk rond QRS-complexen en T-golven met hoge amplitude) om de interferentie van het oorspronkelijke ECG-signaal af te trekken.
Een van de eerste resultaten verkregen met de aftrekkingsmethode is te zien in Fig. 1 . Interferentie werd toegevoegd aan een schoon gesimuleerd ECG-signaal om de fouten en de efficiëntie van de methode te evalueren.
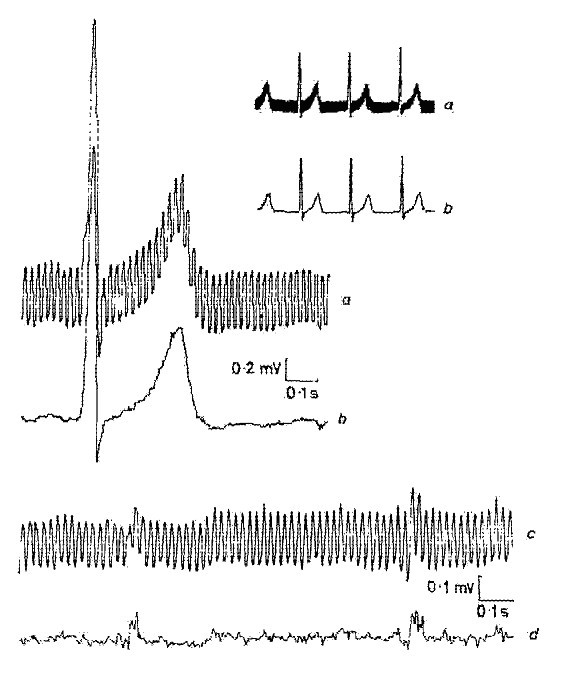
Een van de eerste resultaten verkregen door de aftrekkingsprocedure.
Lineair criterium
Een lineair criterium, Cr, komt gewoonlijk overeen met het tweede verschil van het signaal (mathematische evaluatie van de lineariteit). Het eerste Cr wordt op de volgende wijze gedefinieerd. Zes opeenvolgende eerste verschillen, FD i , worden berekend met behulp van signaalmonsters, X i , met een tussenruimte van één T PL :
FD i = X i+n – X i , voor i = 1 … 6 (1)
De PL-interferentie in de eerste verschillen wordt onderdrukt indien n = f S /f PL . In dit geval is n = 5, aangezien de procedure aanvankelijk werd ontwikkeld voor nominale f PL = 50 Hz en f S = 250 Hz. Voorts worden de maximale FD max- en minimale FD min-waarden genomen om Cr te bepalen:
Cr = | FD max – FD min | <M, (2)
waarbij M de drempelwaarde is.
Typische lineaire en niet-lineaire segmenten worden getoond in Fig. 2. Het echte ECG-signaal (spoor a) wordt gesuperponeerd door interferentie (spoor b). De lineaire segmenten omvatten een laagfrequent signaal en componenten van de netfrequentie. Een frequentiespectrum bij benadering van dergelijke lineaire segmenten wordt getoond in fig. 3.

Typische lineaire en niet-lineaire segmenten in echt ECG-signaal.
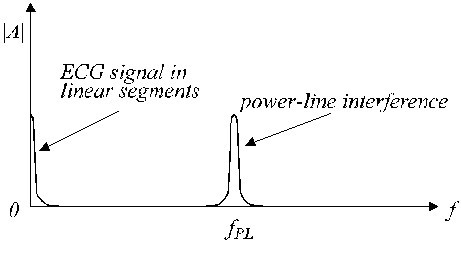
Benaderd frequentiespectrum van een lineair segment.
Dit criterium werkt nauwkeurig, maar kan nauwelijks in real time worden toegepast omdat de uitvoering ervan relatief traag is. Dit nadeel wordt ondervangen door Christov en Dotsinsky, die een gewijzigd criterium van slechts twee opeenvolgende verschillen gebruiken.
Cr = | FDi+1- FD i | <M. (3)
Het eerste monster, dat niet aan vergelijking (3) voldoet, wordt geassocieerd met het begin van een niet-lijnsegment. Bij de overgang van niet-lineair naar lineair moet achtereenvolgens n maal aan vergelijking (3) worden voldaan om voortijdige detectie van het lineaire segment te voorkomen. Het criterium wordt in real time toegepast voor f S = 400 Hz en n = 8.
Later hebben Dotsinsky en Daskalov het criterium gedefinieerd als twee niet-opeenvolgende verschillen:
Cr = |FDi+k- FD i | <M, voor k >1 (4)
Deze benadering maakt de overgang van lineair naar niet-lineair segment preciezer.
Compensatie van PL-amplitudevariaties
Hoe vaker de correcties worden bijgewerkt, hoe beter de amplitudevariaties van het PL worden gecompenseerd. Daarom moet de drempelwaarde voor het lineaire criterium, M, redelijkerwijs minder restrictief zijn, zodat de fouten die ontstaan door middeling van enkele segmenten die van het ideale lineaire signaal afwijken, kleiner zijn dan de fouten die ontstaan als M sporadische bijwerking van de correctie initieert. Aanvankelijk werd M vastgesteld op 160 μV . Later werden heuristische waarden gevonden van M = 150 μV en M = 100 μV .
Lineaire filtering
Voor een oneven aantal monsters n = 2m + 1 in één periode van de PL-interferentie, is de gefilterde waarde:
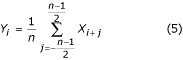
fase-incident met de niet-gefilterde waarde.
In geval van een even getal n = 2m, zijn de twee waarden faseverschoven met de helft van de bemonsteringsperiode:
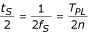
maar worden in fase samenvallend met behulp van de formule
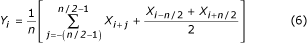
Het is mogelijk om voor de middeling elk tweede, derde of q-ste monster te nemen als n/q een geheel getal is. Afhankelijk van het feit of n/q oneven of even is, wordt respectievelijk vergelijking (7) of (8) gebruikt.

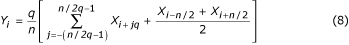
Een speciaal geval van maximale steekproefverkleining doet zich voor met q = n/2 . De bijbehorende formule:
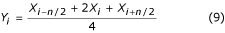
wordt “driepunts”-filter genoemd. Naast vergelijking (8) kan ook de volgende formule
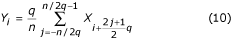
worden toegepast als q even is. In geval van q = n/2 wordt het filter “tweepunts” en wordt voorgesteld door:

Een kleiner aantal monsters in een periode van de interferentie zal leiden tot een steilere helling van de kamfilters en zal de rekentijd verkorten. Deze “voordelen” moeten echter zorgvuldig worden beoordeeld om de Nyquist-regel niet te overtreden bij een grote hoeveelheid van de derde harmonische aanwezig. De andere harmonischen worden buiten beschouwing gelaten, omdat de hoogste oneven harmonischen gewoonlijk worden onderdrukt door laagdoorlaatfilters met een afsnijfrequentie in het bereik van 100-150 Hz, terwijl de even harmonischen praktisch afwezig zijn vanwege de nauwkeurige poolfabricage van de generatoren van de elektriciteitscentrales.
Compensatie van variatie in PL-frequentie
De toegestane afwijking van de nominale PL-frequentie wordt in sommige landen door de normen beperkt tot maximaal 1%. In de praktijk is de afwijking vaak groter. Kumaravel et al. meldden een afwijking van 3%. McManus et al. vonden aanzienlijke veranderingen in de interferentiefrequentie, die gesuperponeerd is op opnamen uit de Common Standards for Electrocardiography (CSE) database.
Frequentievariaties leiden tot een speciaal geval van niet-meervoudige bemonstering met reële n, in plaats van gehele n. Deze complicatie kan worden omzeild als de afwijkingen worden gedetecteerd door continue hardwaremeting van f PL en gecorrigeerd door kleine aanpassingen van het bemonsteringsinterval t S rond zijn nominale (R) waarde, t RS = T RPL /n (hier is T RPL = 20 ms de nominale T PL voor f RPL = 50 Hz). Voor f PL , afwijking tussen 49,5 en 50,1 Hz, liggen de t S variaties in het bereik van 1%, en bijgevolg introduceren zij geen fouten buiten de aanvaarde meetnauwkeurigheid van parameters die gewoonlijk worden gebruikt voor automatische ECG-classificatie.
Een eerste benadering associeert de triggering van elk eerste monster, S 1 , van de reeksen S k (k = 1, 2…n) in de perioden T PL met een willekeurig gekozen maar constante amplitude van de PL-spanning. De volgende monsters, S k (k = 2…n), hebben een tussenpoos van t S , die wordt verkregen door t S = T RTL /n. Voor 50 Hz, en n = 5, is t S = 4 ms. Twee soorten fouten die met deze aanpak worden begaan, zijn bestudeerd door Dotsinsky en Daskalov . De eerste, te wijten aan onregelmatigheden tussen de monsters, kan 1% bereiken bij f S = 400 Hz en 1,2% bij f S = 250 Hz, in geval van 1% afwijking rond de f RPL . De tweede soort fout bedraagt niet meer dan 3% en is een gevolg van de extra verschoven plaats van het gefilterde monster.
Dotsinsky en Daskalov rapporteerden een verbeterde aanpak. De lopende periode T PL wordt gemeten en gedeeld door n. De verkregen t S wordt gebruikt in de daaropvolgende T PL .
Efficiëntiebeoordeling van de procedure
Voorbeelden van de aftrekkingsprocedure worden getoond in Fig. 4 en Fig. 5. De ECG-signalen zijn afkomstig uit de database van de American Heart Association. De signalen worden gefilterd om de 60 Hz-interferentie (PL-frequentie in de VS) te onderdrukken. Vervolgens worden de signalen gemengd met 50 Hz interferentie, amplitude gemoduleerd van 0 tot 3,2 mVp-p met een slew rate van 200 μVs-1. De sporen worden als volgt geïdentificeerd: i) ingangssignaal; ii) gesynthetiseerde interferentie; iii) gemengd signaal; iv) verwerkt signaal; v) verschil tussen het oorspronkelijke en het verwerkte signaal en vi) ingezoomd verschil. De weggelaten componenten omvatten eigenlijk ook elektromyografische (EMG) en andere ruis. Een niet onderdrukt deel van het signaal, samen met kleine reststoringen en vervormingen als gevolg van compromissen met de M-waarde zijn ook aanwezig in de verschillen.
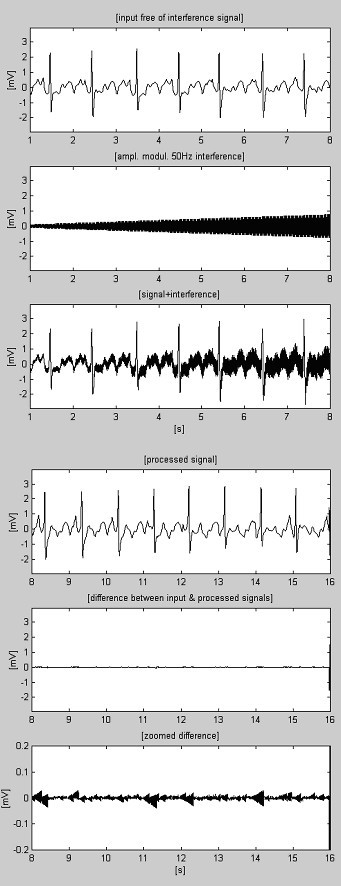
Bewerkte AHA 3004d1-opname.
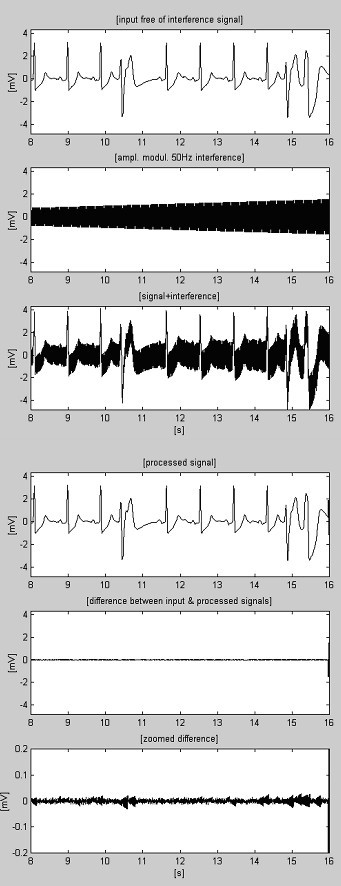
Verwerkte AHA 6007d1-opname.
Twee signalen worden gebruikt om de doelmatigheid van de aftrekkingsprocedure ten opzichte van alleen de interferentie te beoordelen. Het eerste, afkomstig uit onze eigen databank, wordt voorwaardelijk “schoon” genoemd (Fig. 6). Het resultaat vertoont kleine verschillen tussen het ingangssignaal en het verwerkte signaal, visueel te wijten aan de ruis die in het ingangssignaal aanwezig is. Dit resultaat wordt geverifieerd met het tweede gesynthetiseerde signaal, dat geen verstoringen bevat (Fig. 7). Zoals men kan zien, worden geen vervormingen geïntroduceerd. Hetzelfde gesynthetiseerde signaal wordt gesuperponeerd door storing en verwerkt (Fig. 8). Er kan geen reststoring worden gevonden.
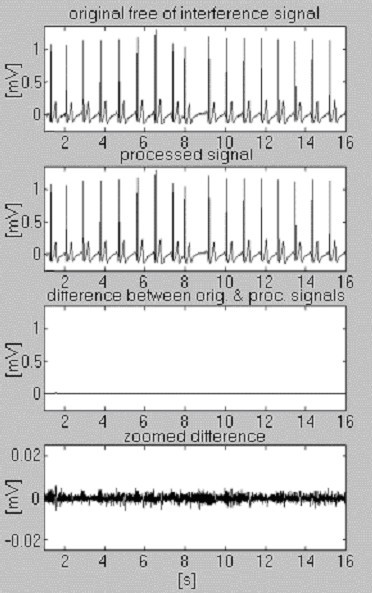
Verwerking van voorwaardelijk ‘schoon’ signaal.
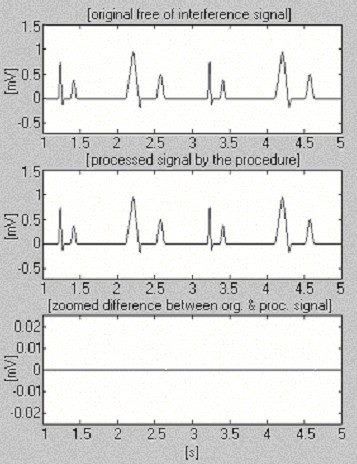
Verwerking van gesynthetiseerd signaal.
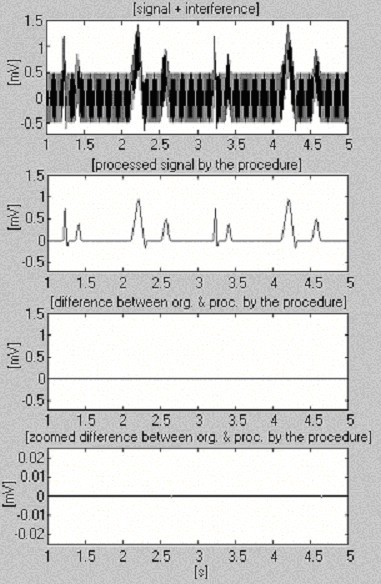
Verwerking gesynthetiseerd signaal+interferentie.
Invloed van EMG-ruis
Soms is de EMG-ruis zo hoog dat het vinden van lineaire segmenten wordt bemoeilijkt. Als gevolg hiervan zullen onnauwkeurige correcties, die niet overeenkomen met de laatste verandering van de interferentieamplitude, fouten veroorzaken (zie de resterende ruis tussen de 11e en 14e s in Fig. 9).
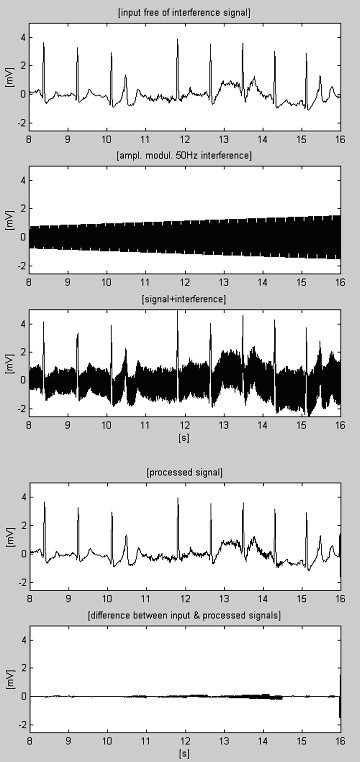
Verwerkt ECG-signaal+EMG-ruis+interferentie.
Een zeer eenvoudige benadering voor de onderdrukking van de invloed van EMG-ruis op de procedure introduceert een extra parallelle buffer waarin lopende gedeelten van het signaal onvoorwaardelijk worden gemiddeld . Deze buffer wordt gebruikt voor nauwkeurige lineariteitsdetectie. Fig. 10 en Fig. 11 tonen de vergelijking van de resultaten zonder en met de parallelle buffer. De sporen “a” stellen het ECG-signaal voor, gemengd met interferentie en EMG-ruis. De lijnen “b” in Fig. 10 en “c” in Fig. 11 geven de overgangen aan van lineaire naar niet-lineaire segmenten (aan-uit functies). Zoals men kan zien, is het gemiddelde signaalgedeelte in Fig. 10 zeer beperkt. Dientengevolge wordt de efficiëntie van de procedure verminderd (Fig. 10c en 10d. Met de parallelle buffer daarentegen kunnen lange lineaire segmenten worden gedetecteerd (fig. 11c) en is de restruis in het verwerkte signaal (fig. 11d) gering. De ruis wordt echter niet volledig onderdrukt omdat een deel ervan deelneemt aan de correctieberekening.
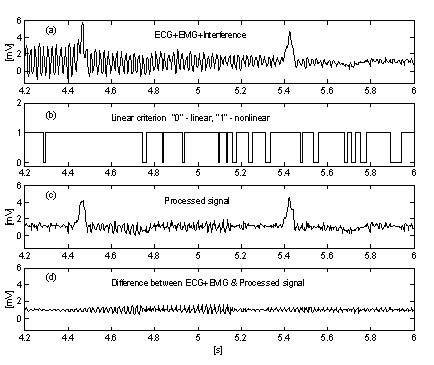
Aftrekking van interferentie+EMG-ruis zonder parallelle buffer.
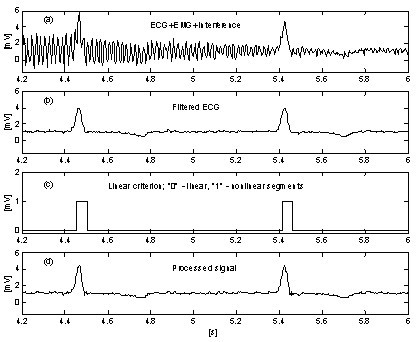
Aftrekking van interferentie+EMG-ruis met parallelle buffer.
Een verdere verbetering van de onderdrukking van EMG-ruis wordt door Christov verkregen door gebruik te maken van de adaptieve drempelwaarde M, die wordt berekend ten opzichte van de ruis-signaalverhouding Rt, gedefinieerd als Rt = S NL /S F , waarbij het ruisniveau S NL gelijk is aan de samenvattende breedte van de niet-lineaire segmenten in een tijdvak S F , dat ongeveer overeenkomt met het RR-interval dat wordt onderzocht. Lineariteit zoeken met een criterium van M = 150 μV voor een “schoon” ECG (fig. 12a) en voor hetzelfde signaal, maar vervuild met EMG-ruis (fig. 12b) tonen verschillende S NL , (fig. 12c en 12d). De methode is ontwikkeld in de MATLAB-omgeving. De aanvangsdrempel M wordt gelijk aan 30 μV gekozen. Vervolgens wordt deze geleidelijk verhoogd tot Rt 10% bereikt, waarna de aftrekkingsprocedure wordt gestart. Het niveau Rt ≤ 0,1 waarde wordt gesuggereerd door de verhouding ‘QRS breedte versus zijn RR interval’, die meestal rond 10% ligt. De eliminatie van zowel interferentie als EMG-ruis kan worden waargenomen in Fig. 13b en 13d, waar M = 420 μV wordt gebruikt. Ter vergelijking wordt het ‘schone’ ECG-signaal verwerkt met M = 35 μV (fig. 13a en 13c).

Ruisniveaus SNL (sporen c en d) in respectievelijk het ‘schone’ ECG-signaal (spoor a) en het EMG-verontreinigde signaal (spoor b).
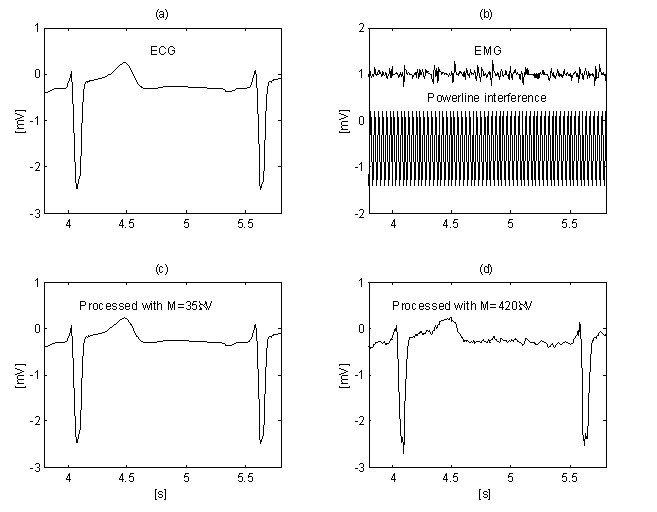
Onderdrukking van storing+EMG-ruis met behulp van adaptieve drempelwaarde M: ‘schoon signaal’ (a) verwerkt met M = 35 μV (c) en verontreinigd signaal (b) onderworpen aan de procedure met M = 420 μV (d).
Lineaire segmenten kunnen niet regelmatig worden gevonden bij patiënten met atriale en ventriculaire fibrillatie. Het volledige behoud van de golfvorm is echter niet noodzakelijk voor de detectie van fibrillatie en daarom kunnen allerlei traditionele filters worden toegepast.
Storingsonderdrukking in hoge-resolutie ECG
De aftrekkingsprocedure is niet direct toepasbaar op het lichaamsoppervlak His-ECG, aangezien de lage amplitude en relatief lage frequentie His-golf niet kan worden onderscheiden in lineaire segmenten. In de praktijk zal de His-golf dus worden onderdrukt of zelfs uit het signaal worden verwijderd. De EMG-ruis is gewoonlijk van grotere amplitude en met een veel hogere frequentie-inhoud dan de oppervlakte-hs-golf. Daarom leidt een eenvoudige wijziging van de drempelwaarde, M, niet tot een aanvaardbare afbakening van lineaire en niet-lineaire segmenten.
Bazhina et al. pasten de volgende wijziging toe. Het begin van het gedetecteerde niet-lineaire segment vóór een QRS-complex wordt 100 ms naar links verschoven, waardoor het gebied van de His-golf standaard wordt gedefinieerd als een niet-lineair segment (fig. 14).
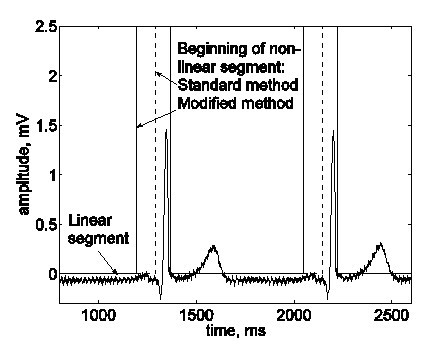
Het begin van een niet-lineair segment dat het QRS-complex omvat, is standaard 100 ms naar links verschoven, om de zone op te nemen waar de His-golf naar verwachting zal verschijnen.
De aftrekkingsprocedure en drie andere methoden: notch filters, spectrale interpolatie , en regressie aftrekken worden getest tegen minimale vervorming van het oorspronkelijke signaal . De subtractie- en de regressie-aftrekprocedure bleken de beste te zijn, aangezien Baratta et al. een soortgelijk concept gebruiken voor ruisschatting in lineaire segmenten. Regressie-aftrekking gaat slecht om met amplitudeveranderingen van de interferentie binnen het huidige segment.
Geval van apparaten op batterijen en computerondersteunde ECG-systemen
De hardwaremeting van f PL , nodig voor compensatie van de interferentiefrequentiemodulatie, is niet uitvoerbaar in apparaten op batterijen en in sommige computerondersteunde ECG-systemen. Dotsinsky en Stoyanov bestudeerden het bereik van frequentieveranderingen van interferentie met constante amplitude, waarvoor het residuele deel tot aanvaardbare niveaus wordt beperkt zonder gebruik van gesynchroniseerde bemonstering. Zij vonden dat een residuele storing van minder dan 20 μVp-p kon worden verkregen met de procedure bij: i) storingsamplitude ≤ 0,4 mVp-p en ii) frequentieverandering met een snelheid ≤ 0,0125 Hzs-1. Aangezien dergelijke eisen aan de stroomvoorziening vaak kunnen worden overschreden, werd een softwarematige storingsmeting ontwikkeld.
Het ECG-signaal wordt eerst verwerkt door een 49-51 Hz banddoorlaatfilter. De amplitudes van twee aangrenzende samples, Br L en Br R , genomen van een positief verlopende helling van de interferentie, gelegen onder en boven de nullijn, worden gemeten (Fig. 15). De afstand, t CP , tussen het kruispunt CP en het rechter monster, Br R , wordt voortdurend berekend door:
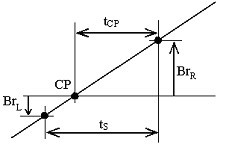
Interferentie nuldoorgang.

In geval van verandering van T PL wordt t S opnieuw bepaald met

Deze aanpak is geïmplementeerd in de MATLAB-omgeving. Voor de bemonsteringsfrequentie f S = 500 Hz en f RPL = 50 Hz is n gelijk aan 10. Het product kn bepaalt de tijd die moet verstrijken alvorens de nieuwe tCP,i + kn te berekenen en te vervangen door de vorige tCP,i. Fig. 16 toont een verwerkt ECG-signaal van 1 mV na vermenging door interferentie met een constante amplitude van 2 mVp-p en een extreem snelle frequentievariatie van 1 Hz per 8 s (eerste spoor). Om de verkregen efficiëntie te beoordelen, wordt ook het ingezoomde verschil zonder gesynchroniseerde bemonstering (laatste spoor) weergegeven.
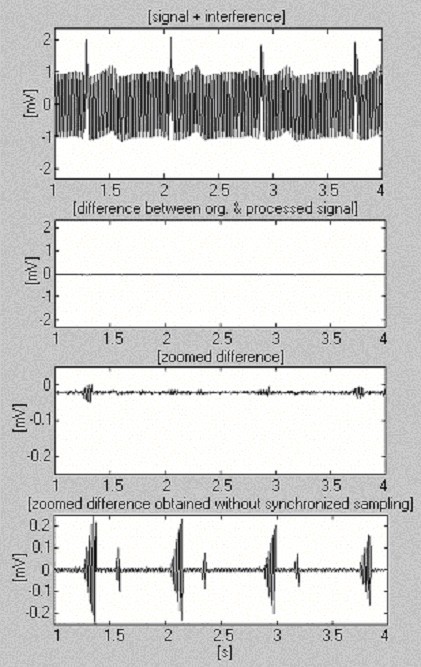
Subtractieprocedure met behulp van software power-line frequentiemeting.
De volgende logische stap die moet worden genomen, bestaat uit: i) het aanhouden van de nominale t S van het ECG-instrument, ii) het opnieuw bemonsteren van het signaal overeenkomstig de huidige gemeten f PL om de interferentie te elimineren en iii) het terugkeren naar de nominale t S . De eerste resultaten van een dergelijke aanpak zijn veelbelovend. Aldus zal de softwarecompensatie van de variabele f PL , evenals een totale implementatie van de aftrekkingsprocedure in een instrument, met inbegrip van automatische aanpassing voor f RPL van 50 of 60 Hz, worden voltooid ongeacht de hardware-circuits en de overeenkomstige software.
Automatische aanpassing aan de nominale PL-frequentie
Een gemeenschappelijk programma voor alternatieve storingstractie in 50 en 60 Hz omgeving leidt tot niet-meervoudige bemonstering, d.w.z. tot reële n. Veel gebruikte waarden van t S voor f RPL = 50 Hz, zoals 250, 500 en 1000 Hz, komen overeen met irrationele n van 4.1(6), 8.3(3) en 4.1(6) indien 60 Hz storing moet worden geëlimineerd. In het omgekeerde geval, f S = 360 Hz, is n = 7,2 vereist. Afgeronde waarden n* kunnen niet worden gebruikt, omdat zij een aanzienlijke fout zouden introduceren.
Een zeer eenvoudige oplossing waarbij f S niet behoeft te worden veranderd, is gevonden door Dotsinsky en Stoyanov . De oorspronkelijke procedure past een kamfilter toe over één periode, T PL , van de interferentie. Het programma loopt dus sneller. In het algemeen kan n worden genomen uit k > 1 hele perioden. De procedure werkt als:
n = kT PL /t S een geheel getal is.
Voor t S = 2 ms (f S = 500 Hz) en f RPL = 50 Hz is de kleinste waarde van k die aan vergelijking (14) voldoet in werkelijkheid k = 1. In het geval van 60 Hz is k echter gelijk aan 3. Nullen behorende bij de subharmonischen 20 en 40 Hz zullen ook verschijnen, maar zij hebben geen invloed op de procedure. Daarom is het voldoende om n te schakelen tussen 10 (k = 1) en 25 (k = 3) om met beide interferenties te werken. Hiertoe controleren twee digitale banddoorlaatfilters het inkomende signaal. Fig. 17 laat zien dat het filter met frequentieband die de interferentie overlapt een orde van grootte hoger uitgangssignaal genereert dan het andere filter.
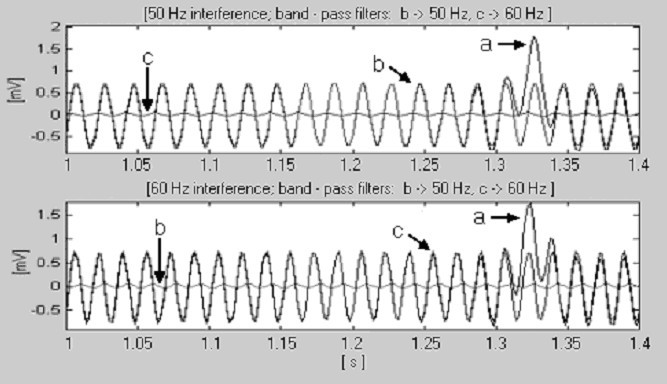
Detectie van de nominale netfrequentie, a) deel van het QRS-complex, b) 50 Hz-interferentie en c) 60 Hz-interferentie.
Ontwikkeling van de theoretische procedure
De theorie van de aftrekkingsprocedure werd verder ontwikkeld door Mihov , Levkov en Mihov , en Mihov e.a. . Zij stelden vier soorten filters voor, geïmplementeerd in een veralgemeende structuur die de problemen kan overwinnen met bijna alle gevallen van niet-meervoudige bemonstering, inclusief interferentiefrequentievariaties, zonder gebruik te maken van gesynchroniseerde AD-conversie.
Het zogenaamde D-filter bij meervoudige bemonstering is gedefinieerd als is Cr in vergelijking (2), waarbij het tweede verschil, D i , wordt verkregen met FD s die op één T PL zijn gespreid:
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
De overdrachtsfunctie van het D-filter heeft nulpunten bij f = 0 en f = f PL Hz, die gelijk is aan 50 Hz in Fig. 18.

Overdrachtsfunctie van D-filter voor fPL = 50 Hz.
Het K-filter beschrijft het voortschrijdend gemiddelde zoals voorgesteld door vergelijkingen (5) en (6). De overdrachtsfunctie is gegeven in fig. 19 voor n = 5 in het geval van oneven multipliciteit.
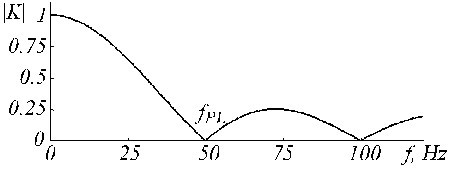
Overdrachtsfunctie van het K-filter voor fPL = 50 Hz en n = 5.
De vergelijking die wordt gebruikt voor de lopende berekening van de storingscomponenten:
B i = X i – Y i (16)
definieert in feite een digitaal filter dat (1-K)-filter wordt genoemd.
Daarnaast zijn de filters opnieuw gedefinieerd voor niet-meervoudige bemonstering, en f S = 250 Hz in combinatie met f RPL = 60 Hz is in aanmerking genomen om de softwareverbetering te illustreren.
Om de nulpunten van de overdrachtsfunctie te behouden, moet het D-filter worden afgetrokken met een correctiefilter met nul bij f = 0 en een versterking van D RPL bij f = f RPL , gelijk aan de versterking van het D-filter voor dezelfde frequentie, f RPL . De synthese van het correctiefilter is gebaseerd op een driepunts hulffilter, gegeven door de vergelijking:

waarbij (n/2)* de afgeronde waarde van n/2 is.
Aangezien A RPL de versterking van het hulffilter is voor f = f RPL , wordt het correctiefilter vermenigvuldigd met de verhouding D RPL /A RPL . Met behulp van de overeenkomstige overdrachtsfuncties worden D RPL en A RPL van tevoren berekend door:
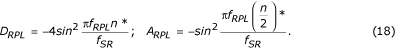
Tot slot wordt het gecorrigeerde D*-filter voorgesteld als

en in fig. 20 weergegeven door spoor “c”, waarbij de sporen “a” en “b” respectievelijk het D-filter en het correctiefilter zijn.
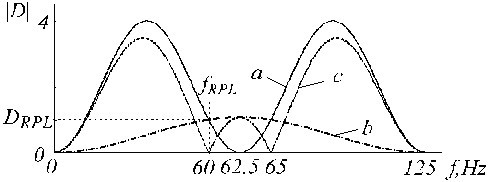
Overdrachtsfuncties van a) D-filter, b) hulpcorrectiefilter en c) gecorrigeerd D-filter.
De overdrachtsfunctie van het K-filter moet nul behouden voor f = f RPL , een eenheidsversterking voor f = 0 en een lineaire faserespons. De procedure voor de correctie van het K-filter is vergelijkbaar met de voorgaande. Een hulpfilter wordt gegeven door de formule die voor de berekening van de correcties wordt gebruikt:
A i = X i – Y i , (20)
De filterversterking is gelijk aan 1 – K RPL voor f = f RPL , waarbij K RPL de K-filterversterking is voor dezelfde frequentie f RPL . Het hulpfilter wordt vermenigvuldigd met K RPL /(1 – K RPL ) en afgetrokken van het K-filter. De vergelijking voor het gecorrigeerde K*-filter is:
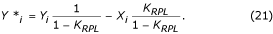
De constante K RPL kan worden geschat door:

voor respectievelijk oneven of even multipliciteit.
Een voorbeeld van K-filtercorrectie is te zien in fig. 21, waar de sporen “a”, “b” en “c” het primaire K-filter, het hulffilter en het gecorrigeerde K*-filter voorstellen.
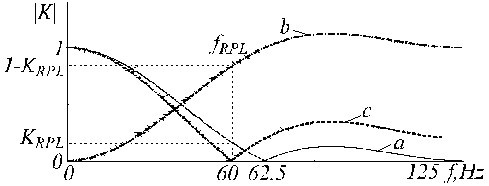
Overdrachtsfunctie van a) het K-filter, b) het hulpcorrectiefilter en c) het gecorrigeerde K-filter.
In geval van niet-meervoudige bemonstering ontstaat er een faseverschil tussen de lopende ECG-monsters en de interferentiecomponenten B i (vergelijking 16) die zich gewoonlijk in een tijdelijke FIFO-buffer (first-in-first-out) bevinden. Daarom moet B i worden gewijzigd en van de ECG-monsters worden afgetrokken tijdens niet-lineaire segmenten. De compensatieprocedure is relatief ingewikkeld. Fig. 22 toont de inhoud van de tijdelijke buffer. Het huidige stoorsignaal, B i-n *, valt niet samen met het herstelde monster, B i . De amplitude ervan moet opnieuw worden berekend om het faseverschil tussen beide te compenseren. Dit wordt bereikt door een nieuw filter met lineaire faserespons en een eenheidsversterking voor f = f RPL, dat het B-filter wordt genoemd. Het wordt gesynthetiseerd uit het bekende K-filter, met een venster dat gelijk is aan de interferentieperiode. In het geval van oneven n* kan het als volgt worden beschreven:
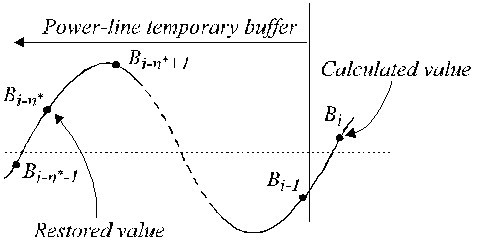
Gereserveerde waarden in de tijdelijke buffer.
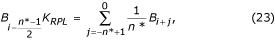
waarbij K RPL de versterking voor de interferentie van het middelingsfilter is, gegeven door vergelijking (22).
De herstelde bufferwaarde B i kan worden berekend door:
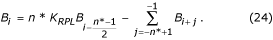
In geval van even n*:
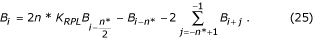
De overdrachtsfunctie van het B-filter wordt getoond in Fig. 23.
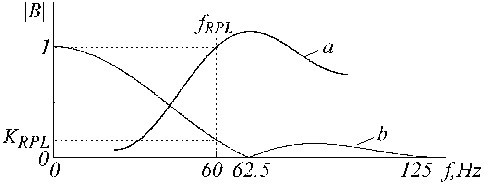
Overdrachtsfuncties van a) het B-filter en b) het bekende K-filter.
De gegeneraliseerde structuur is weergegeven in Fig. 24, waarin de modules van de aftrekkingsprocedure als volgt zijn:
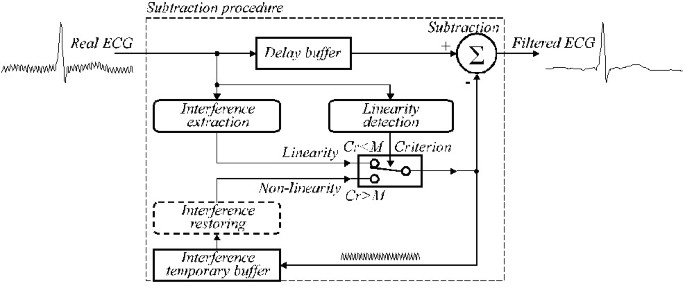
Generaliseerde structuur van de aftrekkingsprocedure.
-
Lineariteitsdetectie. D-filter wordt toegepast om de lineariteit van elke buurt van het signaalmonster te evalueren.
-
Interferentie-extractie. (1-K)-filter wordt gebruikt om de storingscomponent te berekenen.
-
Criterium. De voorwaarde Cr <M stuurt de geëxtraheerde of herstelde PL interferentie naar Subtraction.
-
Interferentie tijdelijke buffer. De geëxtraheerde of herstelde interferentiecomponent die als correctie in niet-lineair segment wordt gebruikt, wordt opgeslagen op de positie die is vergrendeld met de lopende fase van de elektriciteitslijninterferentie.
-
Storingsherstel. B-filter wordt aangeroepen in geval van niet-meervoudige bemonstering om de werkelijke correctiewaarden te herstellen, die moeten worden afgetrokken van de ingangssignaalmonsters in niet-lineaire segmenten.
-
Vertragingsbuffer. Compenseert de vertraging die optreedt bij het D-filter en het (1-K)-filter en is noodzakelijk als de procedure in quasi-real-time wordt uitgevoerd. Anders zou de buffer kunnen worden genegeerd.
-
Subtraction. De geëxtraheerde of herstelde interferentiewaarde wordt van het vertraagde ingangssignaal afgetrokken om een “schoon” ECG-signaal te produceren. In geval van niet-lineariteit wordt bij zowel interferentie-extractie als subtractie het K-filter toegepast.
Een verbeterd algoritme volgens de gegeneraliseerde structuur is off-line getest. De resultaten voor f S = 250 Hz en f RPL = 60 Hz worden getoond in Fig. 25.
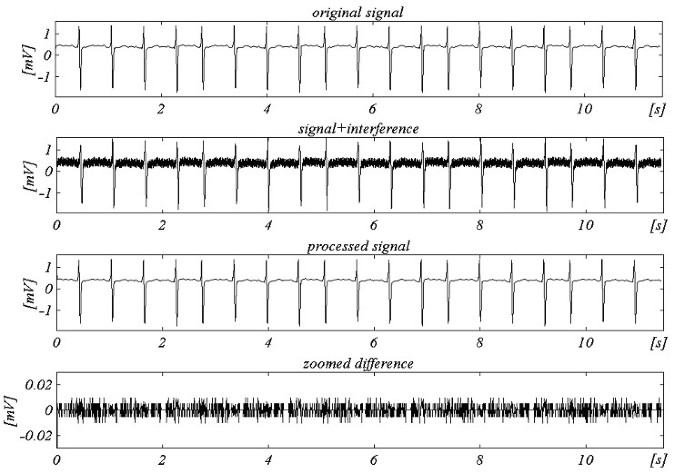
Voorbeeld voor niet-meervoudige bemonstering met fRPL = 60 Hz en fS = 250 Hz.