Trzecie prawo postuluje, że entropia substancji jest zawsze skończona i że zbliża się do stałej, gdy temperatura zbliża się do zera. Wartość tej stałej jest niezależna od wartości jakichkolwiek innych funkcji stanu, które charakteryzują substancję. Dla dowolnej substancji możemy przypisać dowolnie wybraną wartość granicznej wartości temperatury zerowej. Nie możemy jednak przypisać wszystkim substancjom dowolnych entropii temperatury zerowej. Zestaw przyporządkowań musi być zgodny z eksperymentalnie zaobserwowanymi zerowo-temperaturowymi wartościami granicznymi zmian entropii reakcji pomiędzy różnymi substancjami. Dla substancji doskonale krystalicznych wszystkie te entropie reakcji wynoszą zero. Możemy spełnić ten warunek, przypisując dowolną wartość zerowej entropii molowej każdego pierwiastka i stwierdzając, że zerowa entropia dowolnego związku jest sumą zerowych entropii temperaturowych jego elementów składowych. Obliczenia te znacznie się upraszczają, jeśli przyjmiemy, że entropia zerowotemperaturowa każdego pierwiastka wynosi zero. Jest to zasadnicza treść trzeciego prawa.
Oświadczenie Lewisa i Randalla zawiera ten wybór stanu odniesienia zero-entropii dla entropii, określając go jako „stan krystaliczny” każdego elementu w temperaturze zero stopni. W rezultacie, entropia dowolnej substancji w temperaturze zero stopni jest większa lub równa zeru. Oznacza to, że twierdzenie Lewisa i Randalla zawiera konwencję, która ustala graniczną wartość entropii dowolnej substancji w temperaturze zero stopni. W tym względzie twierdzenie Lewisa i Randalla dokonuje zasadniczo arbitralnego wyboru, który nie jest nieodłączną własnością natury. Widzimy jednak, że jest to wybór nad wyraz wygodny.
Przedyskutowaliśmy alternatywne twierdzenia pierwszego i drugiego prawa. Szereg alternatywnych stwierdzeń trzeciego prawa są również możliwe. Rozważamy następujące:
Nie jest możliwe osiągnięcie temperatury zera bezwzględnego.
Twierdzenie to jest bardziej ogólne niż twierdzenie Lewisa i Randalla. Jeśli rozważymy zastosowanie tego twierdzenia do temperatur osiągalnych w procesach z udziałem pojedynczej substancji, możemy pokazać, że wynika ono z twierdzenia Lewisa i Randalla i jest przez nie implikowane.
Właściwości pojemności cieplnej, ∗, odgrywają główną rolę w tych argumentach. Widzieliśmy, że pojemność cieplna jest funkcją temperatury. Chociaż nie jest to użyteczne, możemy zastosować zależność definiującą pojemność cieplną do substancji przechodzącej przemianę fazową i stwierdzić, że pojemność cieplna jest funkcją temperatury. Jeśli pomyślimy o substancji, której pojemność cieplna jest mniejsza od zera, napotkamy sprzeczność naszych podstawowych pojęć o cieple i temperaturze: Jeśli \(q>0\) i \(\/{Delta T}<0\), to musimy mieć \(\Delta T<0\); to znaczy, że ogrzewanie substancji powoduje obniżenie jej temperatury. Krótko mówiąc, teoria, którą opracowaliśmy, zawiera przesłanki, które wymagają \(C_P>0\) dla każdego układu, na którym możemy dokonać pomiarów.
Scharakteryzujmy układ czystej substancji przez jej ciśnienie i temperaturę i rozważmy odwracalne procesy zachodzące pod stałym ciśnieniem, w których możliwa jest tylko praca ciśnienie-objętość. Wówczas ∗ lewa({partial S}/{partial T}} prawa)}_P={C_P}/{T}}) i ∗ dS={C_PdT}/{T}}). Chcemy teraz pokazać, że zgodnie z zastrzeżeniem Lewisa i Randalla, że entropia jest zawsze skończona, pojemność cieplna musi być równa zeru, gdy temperatura spadnie do zera. (Ponieważ zamierzamy pokazać, że trzecie prawo zabrania pomiarów w temperaturze zera bezwzględnego, wniosek ten jest zgodny z naszym wnioskiem z poprzedniego paragrafu). To, że pojemność cieplna spada do zera, gdy temperatura spada do zera, wynika z zależności S={C_PdT}/{T}.\) Jeżeli pojemność cieplna nie spada do zera, gdy temperatura spada do zera, to pojemność cieplna staje się dowolnie duża, gdy temperatura spada do zera, co jest sprzeczne z twierdzeniem Lewisa i Randalla.
Aby rozwinąć ten wynik bardziej jednoznacznie, niech pojemności cieplne w temperaturach T i zero będą odpowiednio \(C_Przelew(T-prawo) \) i \(C_Przelew(0-prawo) \). Ponieważ \(C_Prawa Lewa(T) >0\) dla dowolnego \(T >0\), mamy \(C_Prawa Lewa(T) >0\) dla dowolnego \(T>T^*>0\). Ponieważ entropia jest zawsze skończona, \(\infty >Sleft(T^*prawo)>0\), tak że
>0\]
i
Dla temperatur w sąsiedztwie zera, możemy rozszerzyć pojemność cieplną, z dowolną dokładnością, jako wielomian szeregu Taylora w \(T):
Nierówności stają się
Warunek po lewej stronie wymaga, aby \(C_Prawo(0)=0\).
Możemy postrzegać trzecie prawo jako twierdzenie o pojemnościach cieplnych czystych substancji. Wnioskujemy nie tylko, że \(C_P>0\) dla wszystkich \(T>0\), ale także, że
Ogólniej, możemy wywnioskować odpowiednie twierdzenia dla zamkniętych układów odwracalnych, które nie są czystymi substancjami: \(\left({partial H}/{partial T}}prawo)}_P>0\) dla wszystkich \(T>0\), oraz \(\mathop{mathrm{lim}_{T}do 0} T^{-1}{ \left({partial H}/{partial T}}}prawo)}_P=0\). (Entropia zerowotemperaturowa takich układów nie jest jednak równa zeru.) W poniższej dyskusji opisujemy układ jako czystą substancję. Zasadniczo te same argumenty możemy przedstawić dla dowolnego układu; musimy tylko zastąpić \(C_P}przez \({część H}/{część T}prawa)}_P}. Twierdzenie Lewisa i Randalla mówi, że entropia osiąga stałą wartość w zerze absolutnym, niezależnie od wartości innych funkcji termodynamicznych. Wynika z tego, że entropia w temperaturze zero stopni jest niezależna od wartości ciśnienia. Dla dowolnych dwóch ciśnień, \(P_1\) i \(P_2\), mamy \(S \left(P_2,0\right)-S \left(P_1,0\right)=0\). Pozwalając na \({P=P}_1\) i \(P_2=P+Delta P\) oraz, mamy
dla dowolnego \(\Delta P\).
Gdy mówimy, że zero bezwzględne jest nieosiągalne, mamy na myśli to, że żaden układ nie może przejść żadnej zmiany, w której jego temperatura końcowa wynosi zero. Aby zobaczyć, dlaczego zero bezwzględne musi być nieosiągalne, rozważmy procesy, które mogą obniżyć temperaturę układu. Na ogół mamy do dyspozycji zbiorniki ciepła o różnych temperaturach. Możemy wybrać taki zbiornik, którego temperatura jest najniższa, i doprowadzić układ do tej temperatury przez zwykły kontakt termiczny. To wszystko jest banalnie proste; oczywiście wyzwaniem jest dalsze obniżanie temperatury. Aby tego dokonać, musimy dokonać jakiejś innej zmiany. Niezależnie od tego, jaka to będzie zmiana, nie może być ona wspomagana przez wymianę ciepła z otoczeniem. Kiedy już doprowadzimy system do temperatury najzimniejszej dostępnej części otoczenia, jakakolwiek dalsza wymiana ciepła z otoczeniem może przynieść jedynie efekt przeciwny do zamierzonego. Dochodzimy do wniosku, że każdy proces nadający się do naszego celu musi być adiabatyczny. Ponieważ proces adiabatyczny nie wymienia ciepła z otoczeniem, to proces musi być również procesem możliwym, a więc musi być adiabatyczny, a ponieważ jest adiabatyczny, to musi być adiabatyczny. Rozważmy proces odwracalny i proces nieodwracalny, w którym ten sam układ przechodzi ze stanu określonego przez \(P_1\) i \(T_1\) do drugiego stanu, w którym ciśnienie wynosi \(P_2\). Końcowe temperatury i zmiany entropii w tych procesach są różne. Dla procesu odwracalnego, \(\Delta S=0\); temperaturę końcową oznaczamy jako \(T_2\). Dla procesu nieodwracalnego, \(\Delta S>0\); temperaturę końcową oznaczamy jako \(T^*_2\). Jak się okazuje, zmiana temperatury jest mniejsza dla procesu nieodwracalnego niż dla procesu odwracalnego; czyli \(T_2-T_1<t^*_2-t_1\)>. Równoważnie, proces odwracalny osiąga niższą temperaturę: \({T_2<t}^*_2\)>. Z
możemy obliczyć zmiany entropii dla tych procesów. Dla procesu odwracalnego obliczamy \\ Aby to zrobić, najpierw obliczamy
dla izotermicznej przemiany odwracalnej ze stanu \(P_1\), \(T_1\) do stanu określonego przez \(P_2\) i \(T_1\). Znajdujemy \(T_2\) z
Aby zrozumieć zmianę entropii dla procesu nieodwracalnego, zauważamy najpierw, że istnieje nieskończona liczba takich procesów. Nie ma nic unikalnego w temperaturze końcowej. Biorąc pod uwagę \(P_1\), \(T_1\) i \(P_2\), temperatura końcowa, \(T^*_2\), może mieć dowolną wartość zgodną z właściwościami substancji. Aby określić konkretny proces nieodwracalny, musimy określić wszystkie cztery wielkości \(P_1\), \(T_1\), \(P_2\) i \(T^*_2\). Po wykonaniu tych czynności możemy jednak obliczyć zmianę entropii dla procesu nieodwracalnego,
obliczając zmiany entropii, gdy odwracalnie przenosimy układ wzdłuż izotermicznej dwustopniowej ścieżki od \(P_1\), \(T_1\) do \(P_2\), \(T_1\), a następnie wzdłuż izobarycznej ścieżki od \(P_2\), \(T_1\) do \(P_2\), \(T^*_2\). Obliczenie \(delta S^{irrev}} dla tej odwracalnej ścieżki od \(P_1\), \(T_1\) do \(P_2\), \(T^*_2\) wykorzystuje tę samą logikę, co obliczenie, w poprzednim paragrafie, \(delta S\) dla odwracalnej ścieżki od \(P_1\), \(T_1\) do \(P_2\), \(T_2\). Różnica polega na tym, że ^*_2\) zastępuje ^*_2\) jako górną granicę w całce temperatury. Całka ciśnienia jest taka sama. Mamy więc
Z całki (Delta S^{irrev}>) mamy
Ponieważ całki są takie same i dodatnie, wynika z tego, że \(T^*_2>T_2\), zgodnie z powyższym twierdzeniem.
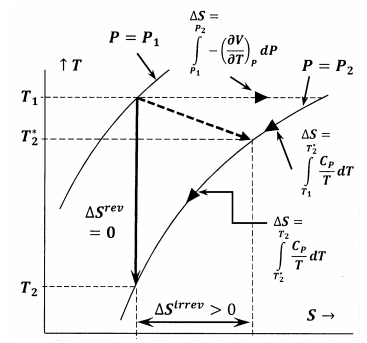
Rysunek 6 przedstawia zależności pomiędzy różnymi wielkościami omawianymi w tym wywodzie. W pierwszym przypadku, Rysunek 6 przedstawia wykres dwóch izobar układu w przestrzeni temperatura-entropia. Oznacza to, że linia oznaczona jako \(P=P_1\) przedstawia zbiór punktów temperatury i entropii, w których układ równowagowy ma ciśnienie \(P_1\); linia oznaczona jako \(P=P_2\) przedstawia pozycje równowagi przy ciśnieniu \(P_2\). Inne linie na tym szkicu reprezentują ścieżki, wzdłuż których układ może ulegać odwracalnym zmianom przy stałej entropii lub stałej temperaturze. Linia przerywana reprezentuje proces nieodwracalny, w którym układ przechodzi ze stanu określonego przez \(P_1\), \(T_1\) do stanu określonego przez \(P_2\), \(T^*_2\). Linia ta jest przerywana, aby przedstawić fakt, że temperatura układu może nie być dobrze określona podczas procesu nieodwracalnego.
Efektywne chłodzenie można osiągnąć za pomocą zmian ciśnienia, jeśli układ jest gazem. Jednakże, dla cieczy i ciał stałych, \({część V}/{część T}}prawa)\) jest mała; w konsekwencji, zmiana temperatury przy odwracalnej zmianie ciśnienia jest również mała. W temperaturach bliskich zera bezwzględnego prawie wszystkie substancje są stałe; aby uzyskać efektywne chłodzenie musimy zmieniać zmienną termodynamiczną, dla której współczynnik temperaturowy ciała stałego jest jak największy. Aby rozważyć ogólny problem obniżania temperatury układu poprzez zmianę czegoś innego niż ciśnienie, musimy rozważyć układ, w którym możliwa jest jakaś forma pracy nieciśnieniowo-objętościowej. Taki układ podlega działaniu dodatkowej siły, a jego energia zmienia się wraz ze zmianą tej siły.
Demagnetyzacja adiabatyczna
Praktyczna metoda, dzięki której uzyskuje się ekstremalnie niskie temperatury, nazywa się demagnetyzacją adiabatyczną. Metoda ta wykorzystuje właściwości paramagnetycznych ciał stałych. W takich ciałach stałych, niesparowane elektrony zlokalizowane na poszczególnych atomach powodują powstanie momentu magnetycznego. Mechanika kwantowa prowadzi do ważnych wniosków na temat interakcji pomiędzy takimi momentami magnetycznymi a przyłożonym polem magnetycznym: W przyłożonym polu magnetycznym, moment magnetyczny pojedynczego atomu jest skwantowany. W najprostszym przypadku może on być ustawiony tylko w dwóch kierunkach; musi być albo równoległy albo antyrównoległy do przyłożonego pola magnetycznego. Gdy moment magnetyczny atomu jest równoległy do pola magnetycznego, energia układu jest mniejsza niż gdy ustawienie jest antyrównoległe. Przyłożone pole magnetyczne wywiera siłę na momenty magnetyczne związane z poszczególnymi atomami. Energia układu zależy od wielkości przyłożonego pola magnetycznego.
Zamiast skupiać się na szczególnym przypadku rozmagnesowania adiabatycznego, rozważmy zmiany energii i entropii związane ze zmianami w uogólnionym potencjale, \({mathit{Phi}}_{theta}), i jego uogólnionym przesunięciu, \(\theta}). (W przypadku demagnetyzacji adiabatycznej, \u200}byłoby to przyłożone pole magnetyczne). Do opisania odwracalnych zmian w tym układzie potrzebne są trzy zmienne. Energię i entropię możemy wyrazić jako funkcje temperatury, ciśnienia i entropii:
E=Eleft(T,P,™theta ™right)™) i S=Sleft(T,P,™theta ™right)™). Różniczka zupełna entropii zawiera człon określający zależność entropii od entropii. Mamy
gdzie piszemy \(C\left(T,P,\theta \right)\), aby podkreślić, że nasze obecne cele wymagają teraz, abyśmy mierzyli pojemność cieplną przy stałym ciśnieniu i stałym \(\theta\).
Dla stałego ciśnienia, P, i stałego przemieszczenia, entropia zależy od temperatury jako
Postulat, że entropia jest skończona w każdej temperaturze implikuje, że pojemność cieplna zależna od ciśnienia i przemieszczenia staje się zerowa w temperaturze zera bezwzględnego. Oznacza to, że w zerze bezwzględnym pojemność cieplna zanika niezależnie od wartości P i ∆t. Argumentacja jest dokładnie taka sama jak poprzednio. Wcześniej pisaliśmy, że \a(C\left(0\right)=0\); dla obecnego uogólnionego przypadku piszemy \a(C\left(0,P,\theta \right)=0\).
Podobnie, z postulatu, że entropia dąży do stałej w zerze bezwzględnym dla wszystkich wartości pozostałych zmiennych termodynamiki, wynika, że dla dowolnych dwóch ciśnień \(P_1\) i \(P_2\), oraz dla dowolnych dwóch wartości uogólnionego przemieszczenia, \Chcemy rozważyć proces, w którym układ przechodzi od najniższej temperatury dostępnej w otoczeniu do jeszcze niższej temperatury. Aby zminimalizować temperaturę końcową, proces ten musi przebiegać adiabatycznie. Musi też być procesem możliwym, a więc ∗ (dS). Dla uproszczenia załóżmy teraz, że przeprowadzamy ten proces przy stałym ciśnieniu, i że układ przechodzi ze stanu określonego przez \(P), \(T_1\), \({theta }_1\) do stanu określonego przez \(P), \(T_2\), \({theta }_2\), gdzie \(T_1>T_2\). czyli T_2=0, więc wynika z tego, że
, gdzie nierówność po prawej stronie wynika z faktu, że >0}. Z tego wynika, że
, co przeczy twierdzeniu Lewisa i Randalla o trzecim prawie. Założenie, że układ może osiągnąć zero bezwzględne prowadzi do sprzeczności twierdzenia Lewisa i Randalla o trzecim prawie. Dlatego, jeśli Lewis i Randall oświadczenie jest prawdziwe, zero bezwzględne jest nieosiągalne.
The converse stosuje się również; to znaczy, z propozycji, że zero bezwzględne jest nieosiągalne, możemy pokazać, że Lewis i Randall oświadczenie jest prawdziwe. W tym celu przekształcamy powyższe równanie dla ∗ (Delta S),
Jeśli teraz założymy, że twierdzenie Lewisa i Randalla jest fałszywe, to wyrażenie po prawej stronie może być mniejsze lub równe zeru. Wtedy całka po lewej stronie może wynosić zero, a wtedy układ może osiągnąć zero bezwzględne. Jeśli twierdzenie Lewisa i Randalla jest fałszywe, to prawdą jest, że układ może osiągnąć zero bezwzględne. Zatem: Jeżeli układ nie może osiągnąć zera bezwzględnego, to twierdzenie Lewisa i Randalla jest prawdziwe.
Rysunki 7 i 8 przedstawiają te idee za pomocą wykresów konturowych w przestrzeni temperatura-entropia. Każdy rysunek przedstawia dwie linie konturowe. Jedna z nich to zbiór wartości temperatury i entropii, wzdłuż których ciśnienie jest stałe i wynosi ∗, a ∗ jest stałe i wynosi ∗. Druga linia konturowa to zbiór wartości temperatury i entropii, wzdłuż których ciśnienie jest stałe i wynosi \(P), a \(\theta\) jest stałe i wynosi \(\theta }_2). Nachylenie linii konturowej wynosi
Bo ponieważ pojemność cieplna jest zawsze dodatnia, to nachylenie jest zawsze dodatnie.
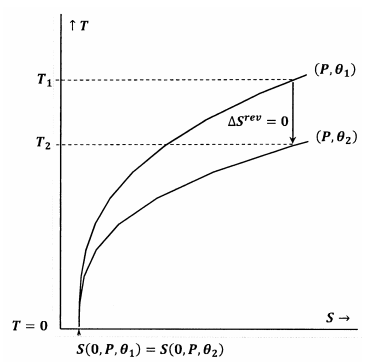
Na rysunku 7 spełnione jest twierdzenie Lewisa i Randalla. Gdy temperatura spada do zera, linie konturu spotykają się przy tej samej wartości entropii; kontury te spełniają zależność
Ścieżka adiabatyczna (pionowa) z konturu dla \(P) i \({theta }_1\) spotyka się z konturem dla \(P) i \({theta }_2\) w dodatniej temperaturze, \(T_2>0\). Ponieważ jest to oczywista prawda dla każdego \P i każdego \P, stan końcowy dla każdego procesu adiabatycznego będzie miał \(T_2>0\). Ponieważ spełnione jest twierdzenie Lewisa i Randalla, układ nie może osiągnąć zera bezwzględnego i odwrotnie.
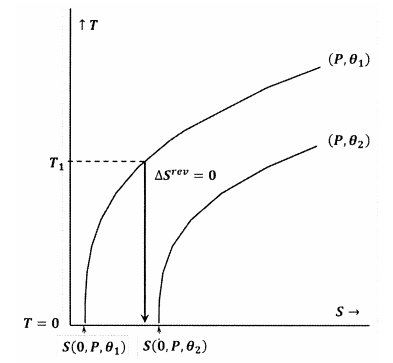
Na rysunku 8 twierdzenie Lewisa i Randalla jest naruszone, ponieważ mamy \(S \left(0,P,\). W tym przypadku, proces adiabatyczny zapoczątkowany z wystarczająco niskiej temperatury początkowej, \(T_1\), osiągnie zero absolutne bez przecinania konturu dla stałych \(P\) i \(\theta }_2\). Ponieważ twierdzenie Lewisa i Randala jest naruszone, układ może osiągnąć zero bezwzględne i na odwrót.