- Introduction
- Materiały i Metody
- Materiał
- Uczestnicy
- Procedury
- Nieliniowa analiza regresji
- Wyniki i dyskusja
- Opisy wyników eksperymentalnych
- Factors Affecting the Maximum Grasping Mass of Human Thumb-Index Finger
- Factors Affecting the Maximum Grasping Diameter of Human Thumb-Index Finger
- Dyskusja
- Wniosek
- Oświadczenie o dostępności danych
- Wkład autorów
- Funding
- Konflikt interesów
Introduction
Porównując z wielopalczastymi zręcznymi rękami, dwupalczasta bioniczna ręka ma prostą strukturę mechaniczną i jest łatwa do planowania ruchu, więc jest zawsze używana w robotach zbierających owoce (Bac et al., 2017; Silwal i in., 2017). Jednak środowisko pracy robotów do zbioru owoców jest niezwykle złożone, takie jak owoce w roślinie różnią się wielkością, kształtem, postawą i pozycją (Li i in., 2019a, b), a istniejące dwupalcowe bioniczne ręce są trudne do spełnienia wymagań chwytania zbioru owoców (Li i in., 2013), więc roboty te nie są jeszcze używane do praktycznego zbioru owoców do tej pory. Z pomocą koordynacji mózgu i oka, osoby są zawsze uważane za wiarygodnych wykonawców, gdy są w stanie wykonać zadania chwytania, przenoszenia i uwalniania docelowego owocu przy użyciu tylko kciuka i palca wskazującego, a ogólna wydajność tego stabilnego systemu manipulacji jest rozsądna. Ludzka ręka jest potężnym wielofunkcyjnym narzędziem, a badanie jej możliwości pomaga badaczom określić rozsądną masę i rozmiar chwytu dla bionicznej ręki robotycznej, zamierzającej odwzorować jej zdolności (Feix i in., 2014; Chen i in., 2019). Z punktu widzenia ergonomii, projektanci robotów do zbioru owoców muszą zrozumieć możliwości kooperacyjnego chwytania ludzkiego palca wskazującego kciuka i ilościową korelację między długością palca a możliwościami chwytania dla nowo zaprojektowanych dwupalcowych bionicznych rąk, tak aby poprawić ich wydajność chwytania (Yussof i Ohka, 2012; Wang i Ahn, 2017).
Badania podkreślające zachowania chwytania ludzkiego palca wskazującego kciuka zostały opublikowane w ciągu ostatniej dekady. Niektórzy badacze ujawnili, że na stabilność chwytu podczas manipulacji wpływ miały przede wszystkim masa obiektu, względna krzywizna i siła tarcia między opuszkami palców a powierzchnią obiektu oraz odległość między dwoma punktami kontaktowymi, gdy obiekt był szczypany przez palec wskazujący kciuka (Li i in., 2013; Luciw i in., 2014). Biegstraaten i wsp. (2006) stwierdzili, że ruchy sięgania i podnoszenia były dość niezależne, gdy obiekt był chwytany za pomocą chwytu precyzyjnego (Biegstraaten i wsp., 2006). Vigouroux et al. (2011) zaproponowali, że kiedy ludzki kciuk-palec wskazujący chwytał przedmioty o różnej szerokości, postawy stawów palców, siła mięśni i siła chwytu różniły się znacząco w zależności od szerokości przedmiotu, a interesującym wynikiem było to, że stosunek siły mięśniowej do siły chwytu głównych mięśni zginaczy pozostawał szczególnie stabilny w odniesieniu do szerokości, podczas gdy stosunek innych mięśni znacznie się różnił. Co więcej, przeprowadzono również różne badania dotyczące zdolności chwytania pięcioma palcami przez człowieka (Vigouroux i in., 2011). Eksioglu (2004) wykazał, że optymalna rozpiętość chwytu w odniesieniu do antropometrii dłoni danej osoby była o około 2 cm krótsza niż zmodyfikowana długość kroku kciuka, w oparciu o kryteria oceny maksymalnej dobrowolnej izometrycznej siły chwytu, aktywności mięśniowej i subiektywnej oceny. Seo i Armstrong (2008) wykazali, że w przypadku chwytania cylindrycznych rękojeści w pozycji power grip, stosunek średnicy rękojeści do długości dłoni może wyjaśnić 62%, 57% i 71% wariancji odpowiednio siły chwytu, siły normalnej i powierzchni styku, Seo i Armstrong (2008). Li i wsp. (2010) przewidywali, że obwód dłoni, spośród kilku parametrów antropometrycznych, takich jak wzrost, masa ciała, nadgarstek i przedramię, długości dłoni i dłoni, miał najsilniejszą korelację z maksymalną siłą chwytu. Bansode i wsp. (2014) wykazali, że siła chwytu ręki dominującej u mężczyzn i kobiet miała istotną dodatnią korelację z wiekiem, wzrostem, wagą i wskaźnikiem masy ciała oraz rozpiętością ręki dominującej, natomiast nie miała oczywistej korelacji z obwodem talii i stosunkiem talii do bioder. Feix i wsp. (2014) stwierdzili, że optymalna zdolność chwytna ludzkiej ręki wynosiła mniej niż 500 g w przeliczeniu na masę, a szerokość przedmiotu w miejscu chwytu była mniejsza niż 7 cm.
Podsumowując, w tej dziedzinie dokonał się znaczny postęp. Niemniej jednak, mniej uwagi poświęcono zdolności do współpracy kciuka i palca wskazującego oraz czynnikom wpływającym na tę zdolność. Oznacza to, że istnieje luka techniczna w ergonomicznym projektowaniu zrobotyzowanych dłoni, których celem jest odtworzenie zdolności ludzkiej ręki. Dlatego też, na podstawie istniejących danych literaturowych, przeprowadziliśmy badania mające na celu zbadanie wpływu cech ludzkiego ciała (np, wiek, płeć, wzrost, używana ręka, suma długości kciuka i palca wskazującego oraz stosunek długości palca wskazującego do długości kciuka) na zdolności chwytne palca kciuka i palca wskazującego, a mianowicie maksymalną masę chwytną i średnicę palca kciuka i palca wskazującego przy użyciu metody analizy regresji nieliniowej wielokrotnej.
Materiały i Metody
Materiał
Aby zbadać zdolności kooperacyjnego chwytania ludzkiego palca wskazującego kciuka, w sierpniu 2017 roku wyprodukowano 20 różnych mas litych cylindrów i 15 różnych średnic zewnętrznych pierścieni jako obiekty chwytane. Masywne cylindry o średnicy dc równej 40 mm wykonano ze stali węglowej C45 posiadającej następujące właściwości: gęstość 7,85 g/cm3 i chropowatość powierzchni Ra = 0,1 μm (rys. 1A). Pierścienie o wysokości hr równej 40 mm wykonane były z akrylu i charakteryzowały się gęstością 1,2 g/cm3 oraz chropowatością powierzchni Ra = 0,05 μm (rys. 1B). Parametry użytkowe litych cylindrów i pierścieni, takie jak ich wysokości, średnice i masy, zestawiono w tabeli 1. Cylindry pełne wykorzystano do badania wpływu cech ciała ludzkiego na maksymalną masę obiektów, które można uchwycić palcem wskazującym kciuka, natomiast pierścienie wykorzystano do badania wpływu cech ciała ludzkiego na maksymalną średnicę obiektów, które można uchwycić palcem wskazującym kciuka. Wieloczynnikowe testy uwalniania chwytów przeprowadzono w ciągu 72 h w temperaturze pokojowej (24 ± 1°C, 50-55% RH).
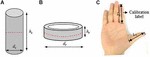
Rysunek 1. Rozmiary chwytanych obiektów i rozmiary dłoni: (A) walec pełny, gdzie dc i hc oznaczają średnicę i wysokość, (B) pierścień, gdzie dr i hrden oznaczają średnicę zewnętrzną i wysokość, (C) rozmiary dłoni, Li – długość palca wskazującego, Lt – długość kciuka.
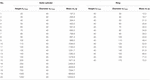
Tabela 1. Charakterystyka geometryczna chwytanych obiektów.
Uczestnicy
W sumie 108 ochotników (54 mężczyzn i 54 kobiety) zostało zrekrutowanych z Henan Polytechnic University, Przedszkola HPU i Szkoły Podstawowej Hexiang do udziału w testach uwalniania chwytu w tym badaniu. Ich charakterystyka była następująca (średnia): wiek, 11,9 (6,8) lat; wzrost, 141,5 (23,8) cm; długość kciuka, 41,9 (7,7) mm i długość palca wskazującego, 56,6 (10,0) mm. Wszystkim uczestnikom przedstawiono szczegółowy opis celów i wymagań eksperymentu, a następnie uzyskano pisemną świadomą zgodę od uczestników powyżej 16. roku życia oraz od rodziców uczestników poniżej 16. roku życia. Wszyscy ochotnicy byli praworęczni, mieli prawidłowy słuch i wzrok od skorygowanego do normalnego, nie mieli w przeszłości urazów rąk, chorób psychicznych ani niepełnosprawności fizycznej. Badanie przeprowadzono zgodnie z zasadami Deklaracji Bazylejskiej i zaleceniami Establishment of Institutional Ethics Committees in China.
Procedury
Uczestnicy umyli ręce wodą z mydłem i osuszyli je ręcznikiem około 5 min przed badaniami. Wzrost każdego uczestnika mierzono za pomocą składanej linijki z dokładnością do 1 mm. Każdemu uczestnikowi ułatwiono naklejenie na dłonie naklejki kalibracyjnej, a kciuk i palec wskazujący otwarto w celu wykonania zdjęcia aparatem cyfrowym (Canon IXUS 95IS) z wierzchu dłoni (ryc. 1C). Przechwycone obrazy zostały przesłane do komputera, a następnie przetworzone przez Digimizer Version 4.2.6.0 w celu wyodrębnienia długości obu palców. Długości kciuka i palca wskazującego mierzono na podstawie odległości od proksymalnej bruzdy zgięciowej palca do czubka odpowiedniego palca (Rysunek 1C), co było zgodne z Kanchan i Krishan (2011), Ishak et al. (2012) oraz Jee et al. (2015). Następnie chwycone obiekty umieszczono na stole, a każdemu uczestnikowi polecono usiąść na krześle biurowym przed stołem z prawym ramieniem górnym równolegle do tułowia, łokciem opartym na prawym udzie i przedramieniem wysuniętym do przodu. Uczestnik został poproszony o podniesienie i przeniesienie przedmiotu z jednej pozycji do drugiej, używając naturalnie kciuka i palca wskazującego prawej ręki. 15 s później uczestnik przenosił przedmiot z powrotem używając kciuka i palca wskazującego lewej ręki. Podczas chwytania palec środkowy, palec serdeczny, mały palec i dłoń nie mogły dotknąć przedmiotu.
Współpracujący proces chwytania przez ludzki kciuk i palec wskazujący był zachowaniem związanym z koordynacją ręka-mózg-oko i może być podzielony na pięć kroków (rysunek 2). 1. krok: lokalizacja i wyczucie obiektu przez system wizyjny z przewodnictwem mózgu; 2. krok: mózg przetwarza informacje uzyskane z systemu wizyjnego i podejmuje strategiczną decyzję (np, rodzaj chwytu wstępnego, siła chwytu i pozycja chwytu) dla stabilnego uchwycenia obiektu; 3. krok: mózg wydaje polecenie ręce, aby dosięgła i chwyciła obiekt; 4. krok: informacja z czujników dotykowych została przekazana do mózgu w celu podjęcia dalszej decyzji i jeśli to konieczne, postawa i siła chwytu zostaną skorygowane poleceniem mózgu; 5. krok: ręka chwyta obiekt stabilnie i przenosi go w inne miejsce.
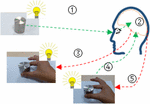
Rysunek 2. Kooperacyjne zachowanie chwytające ludzkiego kciuka i palca wskazującego.
W tym eksperymencie, chwytanymi obiektami były stałe cylindry o różnych masach (Rysunek 1A) i pierścienie o różnych rozmiarach (Rysunek 1B). Każdy z uczestników chwytał stałe cylindry na podstawie ich masy w kolejności od lekkiej do ciężkiej, a następnie chwytał pierścienie na podstawie ich średnicy zewnętrznej w kolejności od małej do dużej. Maksymalna masa chwytna ludzkiego palca wskazującego kciuka wskazywała maksymalną masę obiektów, które mogą być uchwycone palcem wskazującym kciuka. Maksymalne średnice chwytania ludzkiego palca wskazującego kciuka wskazywały maksymalną średnicę obiektów, które mogą być uchwycone palcem wskazującym kciuka. Po każdym zadaniu chwytania, wynik chwytania, czyli sukces lub porażka, był dokładnie zapisywany przez wykwalifikowanego obserwatora. Próbę chwytu uznawano za udaną, jeśli proces uwalniania chwytu był stabilny i nie wystąpił względny poślizg pomiędzy palcem wskazującym, kciukiem i obiektem; w przeciwnym razie, próbę uznawano za nieudaną. W sumie, było 7560 prób chwytania (108 ochotników × 2 ręce × 20 pełnych cylindrów + 108 ochotników × 2 ręce × 15 pierścieni) w eksperymencie.
Nieliniowa analiza regresji
W tym badaniu, metoda nieliniowej analizy regresji jest używana do znalezienia dwóch potencjalnych modeli matematycznych zależności pomiędzy zmiennymi zależnymi (mianowicie, maksymalna masa chwytania i średnica palca wskazującego kciuka) a zestawem zmiennych niezależnych (np, wiek, płeć, używana ręka oraz suma długości palców kciuk-indeks, stosunek długości palca wskazującego do kciuka). Ponieważ kciuk i palec wskazujący człowieka współwystępują ze sobą, a ich długości wykazują wieloliniowość, do charakterystyki długości kciuka i palca wskazującego w analizie regresji wybrano dwa względne parametry niezależne: sumę długości kciuka i palca wskazującego oraz stosunek długości palca wskazującego do długości kciuka. Ze względu na przewidywaną przez Abdel-Malek i wsp. (1990) silną korelację między wzrostem a sumą długości palców, w poniższej analizie regresji uwzględniono sumę długości palców, natomiast nie wzięto pod uwagę wzrostu. Cechy ciała człowieka, takie jak wiek i suma długości palców kciuka i wskaziciela, uznano za pierwotne zmienne niezależne, a maksymalną masę chwytu i średnicę palca kciuka i wskaziciela ustawiono odpowiednio jako pierwszą i drugą zmienną zależną. Po przeprowadzeniu eksperymentów wyznaczono liniowe (np. y = kx) i nieliniowe (np, y = kx2, y = klnx) zależności funkcyjne między wiekiem a maksymalną masą chwytu, między sumą długości palców wskazujących kciuka a maksymalną masą chwytu, między wiekiem a maksymalną średnicą chwytu oraz między sumą długości palców wskazujących kciuka a maksymalną średnicą chwytu, zostały oszacowane przy użyciu „estymacji krzywej” programu IBM SPSS Statistics 24.0 (wersja 24.0, IBM Corporation, Stany Zjednoczone), a następnie porównane w celu wybrania optymalnej zależności funkcyjnej między tymi dwiema zmiennymi na podstawie skorygowanego współczynnika determinacji R2. Większy R2 wskazywał, że odpowiadająca mu zależność funkcyjna jest bardziej odpowiednia do dopasowania danych eksperymentalnych między dwiema zmiennymi. The constant was not included in each regression equation.
After the optimal functions between the original quantitative independent variables and the dependent variables were obtained, each non-linear function was regarded as a new independent variable to be used in the following multiple linear regression analysis and the significance level was set at 0.05. Ponieważ płeć i używana ręka były zmiennymi kategorycznymi, przed analizą regresji liniowej dwa poziomy płci, a mianowicie mężczyzna i kobieta, zostały zakodowane jako „0” i „1”, odpowiednio, a dwa poziomy używanej ręki, a mianowicie lewa ręka i prawa ręka, zostały również zakodowane jako „0” i „1”, odpowiednio. W końcu, zastosowano analizę regresji liniowej wielokrotnej, aby skonstruować dwa potencjalne modele matematyczne. Stała nie była uwzględniana w każdym modelu regresji. Test dobroci dopasowania został użyty do zmierzenia, jak dobrze obserwowane dane odpowiadają każdemu modelowi regresji, test F został użyty do zbadania ogólnej istotności każdego modelu regresji, a test t został użyty do określenia, czy zmienna niezależna miała statystycznie istotny wpływ na zmienną zależną w każdym modelu.
Wyniki i dyskusja
Opisy wyników eksperymentalnych
Rysunek 3 przedstawia maksymalne masy chwytne ludzkiego kciuka-palca wskazującego w różnych warunkach charakterystyki ciała człowieka (np, płeć, używana ręka, wiek i suma długości palców kciuka i wskazującego). W tym badaniu maksymalne masy chwytne palca wskazującego kciuka uczestników wahały się od 690,2 do 9859,6 g. Maksymalne masy chwytne palca wskazującego kciuka mężczyzn wynosiły 5057,6 ± 2695,6 g (średnia ± odchylenie standardowe) i były istotnie wyższe niż u kobiet 3265,5 ± 1853,5 g (ryc. 3A). Nie stwierdzono natomiast istotnej różnicy w maksymalnych masach chwytnych palca wskazującego kciuka w lewej i prawej ręce uczestników; maksymalne masy chwytne palca wskazującego kciuka lewej ręki wynosiły 4102,7 ± 2449,4 g i były nieco niższe od mas chwytnych palca wskazującego prawej ręki 4220,5 ± 2513,1 g (ryc. 3B). W tym badaniu wiek uczestników wynosił od 3∼27 lat, a suma długości kciuka i palca wskazującego wahała się od 56,9 do 132,6 mm. Oczywiście maksymalne masy chwytne palca kciuka i palca wskazującego uczestników miały nieliniowy (np. funkcja kwadratowa, funkcja logarytmiczna) trend rosnący wraz ze wzrostem wieku i sumy długości kciuka i palca wskazującego (ryc. 3C,D).
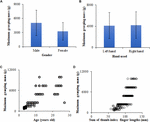
Rycina 3. Maksymalne masy chwytne palca wskazującego kciuka człowieka w różnych warunkach charakterystyki ciała człowieka: (A) zależność między płcią a maksymalną masą chwytną (Mean ± Standard Deviation), (B) zależność między hand-used a maksymalną masą chwytną (Mean ± Standard Deviation), (C) zależność między wiekiem a maksymalną masą chwytną, (D) zależność między sumą długości palca wskazującego kciuka a maksymalną masą chwytną.
Rysunek 4 przedstawia maksymalne średnice chwytne palca wskazującego kciuka człowieka w różnych warunkach charakterystyki ciała człowieka (np, płeć, używana ręka, wiek i suma długości palców kciuka i wskazującego). W tym badaniu, maksymalne średnice chwytne palca wskazującego kciuka uczestników wahały się od 70 do 170 mm. Maksymalne średnice chwytne palca wskazującego kciuka u mężczyzn wynosiły 129,0 ± 22,2 mm i były nieco większe niż u kobiet 119,9 ± 25,2 mm (ryc. 4A). Maksymalne średnice chwytne palca wskazującego kciuka lewej ręki wynosiły 124,0 ± 24,1 mm i były prawie takie same jak u prawej ręki (Ryc. 4B). Podobnie jak na ryc. 3C,D, maksymalne średnice chwytne palca wskazującego kciuka uczestników również wykazywały nieliniową (np. funkcja kwadratowa, funkcja logarytmiczna) tendencję wzrostową wraz ze wzrostem wieku i sumy długości kciuka i palca wskazującego (ryc. 4C,D).
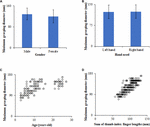
Rysunek 4. Maksymalne średnice chwytne palca wskazującego kciuka człowieka w różnych warunkach charakterystyki ciała człowieka: (A) zależność między płcią a maksymalną średnicą chwytu (Średnia ± odchylenie standardowe), (B) zależność między używaną ręką a maksymalną średnicą chwytu (Średnia ± odchylenie standardowe), (C) zależność między wiekiem a maksymalną średnicą chwytu, (D) zależność między sumą długości palca wskazującego kciuka a maksymalną średnicą chwytu.
W tabeli 2 zestawiono skorygowane współczynniki determinacji modeli regresji liniowej i nieliniowej między ilościowymi zmiennymi niezależnymi i zależnymi. Porównując skorygowane współczynniki determinacji trzech rodzajów funkcji, funkcja liniowa zapewniała optymalny związek funkcjonalny między wiekiem a maksymalną masą chwytu oraz między sumą długości palców wskazujących kciuka a maksymalną średnicą chwytu; funkcja kwadratowa dawała optymalne związki funkcjonalne między sumą długości palców wskazujących kciuka a maksymalną masą chwytu; a funkcja logarytmiczna zapewniała optymalny związek funkcjonalny między wiekiem a maksymalną średnicą chwytu. Wyniki te zostały wykorzystane w poniższej analizie regresji.

Tabela 2. Skorygowane współczynniki determinacji modeli regresji między zmiennymi niezależnymi i zależnymi.
Factors Affecting the Maximum Grasping Mass of Human Thumb-Index Finger
Nieliniowy model regresji zależności maksymalnej masy chwytu od płci, wieku i sumy długości palców kciuka i palca wskazującego przedstawiono w równaniu 1. Skorygowany współczynnik determinacji, oznaczany jako R2, wyniósł 0,97, co sugeruje, że model dobrze dopasował się do danych i wskazuje, że model ten może wyjaśnić 97% wariancji maksymalnej masy chwytu przewidywanej przez płeć, wiek i sumę długości palców wskazujących kciuka. Na podstawie testu F stwierdzono, że ogólne dopasowanie było istotne (P < 0,05). Testy t wykazały, że maksymalna masa przedmiotów, które uczestnicy mogli uchwycić za pomocą palca wskazującego kciuka zależała od płci, wieku i sumy długości palców wskazujących kciuka (P < 0,05), ale nie od używanej ręki i stosunku długości palca wskazującego do kciuka (P > 0.05).
gdzie Mmax – maksymalna masa chwytna, g; G – płeć; A – wiek uczestników, lata; i Lo – suma długości palców, mm.
Wiek uczestników wahał się od 3∼27 lat, co jest na etapie wzrostu i rozwoju mięśni człowieka (Lexell i in., 1992), zatem wiek wykazywał dodatni istotny wpływ na maksymalną masę chwytną palca wskazującego kciuka człowieka. Suma długości kciuka i palca wskazującego była pozytywnie związana z maksymalną masą chwytną palca wskazującego kciuka człowieka, co wynika z faktu, że uczestnicy o dużych dłoniach mają długie palce i mają tendencję do posiadania dużej siły mięśniowej (Seo i Armstrong, 2008). Wartości G = 0 lub 1, czyli mężczyzna lub kobieta, zostały podstawione do równania 1, aby opisać maksymalne masy chwytne uczestników. Różnica w maksymalnych masach chwytnych kciuka i palca wskazującego mężczyzn i kobiet wynosiła 1070,5 g. Podobne wyniki badań wykazały, że siła chwytu mężczyzn była znacząco wyższa niż siła chwytu kobiet (Puh, 2009), a długość dłoni miała znaczący wpływ na siłę chwytu ludzkich pięciopalcówek (Li i in., 2010). Istotny związek między płcią a maksymalną masą chwytną dwóch palców można przypisać temu, że maksymalna siła dobrowolnego skurczu u mężczyzn jest zawsze większa niż u kobiet o podobnym wzroście (Shurrab i in., 2017). Dlatego też zwiększenie maksymalnej siły dobrowolnego skurczu może poprawić maksymalną masę chwytną ludzkich palców dwugłowych. Siła chwytu jest podobnym parametrem do maksymalnej masy chwytnej dla pomiaru zdolności chwytnej ludzkich palców. Wyniki te pokazały, że suma długości palców i maksymalna siła dobrowolnego skurczu mogą wspólnie wpływać na maksymalną masę chwytną palca wskazującego kciuka, co sugeruje, że te dwa czynniki powinny być rozważane razem w celu poprawy maksymalnej masy chwytnej zrobotyzowanych rąk podczas projektowania ergonomicznego.
Factors Affecting the Maximum Grasping Diameter of Human Thumb-Index Finger
Nieliniowy model regresji dla zależności maksymalnej średnicy chwytu od wieku, sumy długości palców kciuk-indeks oraz stosunku długości palca wskazującego do kciuka przedstawiono w równaniu 2. Skorygowany współczynnik determinacji, oznaczany jako R2, wyniósł 0,99, co świadczy o tym, że model dobrze dopasował się do danych i może wyjaśnić 99% wariancji maksymalnej średnicy chwytu przewidywanej przez wiek, sumę długości palców wskazujących kciuka i stosunek długości palca wskazującego do kciuka. Na podstawie testu F stwierdzono, że ogólne dopasowanie było istotne (P < 0,05). Testy t wykazały, że maksymalna średnica przedmiotów, które uczestnicy mogli uchwycić za pomocą palca wskazującego kciuka zależała od wieku, sumy długości palców wskazujących kciuka i stosunku długości palca wskazującego do długości kciuka (P < 0,05), ale nie od płci i używanej ręki (P > 0,05).
gdzie Dmax – maksymalna średnica chwytu, mm; Lo – suma długości kciuka i palca wskazującego, mm; Lr – stosunek długości palca wskazującego do kciuka.
Suma długości kciuka i palca wskazującego wahała się od 56,9 do 132,6 mm, a stosunek długości palca wskazującego do kciuka wahał się od 1,09 do 1,65. Suma długości kciuka i palca wskazującego była dodatnio proporcjonalna do maksymalnej średnicy chwytu. Im większa suma długości palców kciuka i wskazującego, tym większa rozpiętość między opuszkami palców, a więc tym większa maksymalna średnica chwytu uczestników posługujących się palcem kciuka i wskazującym. Gdy suma długości kciuka i palca wskazującego zwiększała się o 1 mm, maksymalna średnica chwytu palca kciuka i palca wskazującego zwiększała się o 0,98 mm. Gdy stosunek długości palca wskazującego do kciuka wzrósł o 0,01, maksymalna średnica chwytu palca wskazującego wzrosła o 0,0967 mm. Stosunek długości palca wskazującego do kciuka był dodatnio związany z maksymalną średnicą chwytu, co wskazywało, że kombinacja krótkiego kciuka i długiego palca wskazującego zwiększy maksymalną średnicę chwytu palca wskazującego. Głównym powodem jest to, że gdy obiekt jest chwytany przez dwa palce, szczególnie w typie power-grasp, krótki kciuk łatwo służy jako punkt podparcia, aby dopasować się do długiego palca wskazującego w obejmowaniu konturu obiektu w celu utworzenia płaszczyzny zamykającej siłę. Krótki kciuk nie jest łatwo ograniczany przez kształt obiektu i stabilny chwyt z zamknięciem siłowym może być osiągnięty w płaszczyźnie kontaktu w oparciu o kryterium stabilności chwytu, które zostały przedstawione przez Li et al. (2013). W literaturze jest niewiele informacji na ten temat.
Dyskusja
Równanie 1 w punkcie „Factors Affecting the Maximum Grasping Mass of Human Thumb-Index Finger” ilościowo opisywało zależność pomiędzy sumą długości kciuka i palca wskazującego a maksymalną masą chwytną. Podczas opracowywania bionicznej, dwupalczastej, zrobotyzowanej ręki, jeśli znane są masy potencjalnych obiektów docelowych, optymalna długość zrobotyzowanego kciuka i palca wskazującego może być wyznaczona na podstawie równania 1 oraz dodatkowego warunku: średni stosunek długości palca wskazującego do kciuka wynosi 1,36. Podobnie, równanie 2 w rozdziale „Czynniki wpływające na maksymalną średnicę chwytu ludzkiego kciuka i palca wskazującego” ilościowo opisywało zależność pomiędzy sumą długości kciuka i palca wskazującego, stosunkiem długości palca wskazującego do długości kciuka i maksymalną średnicą chwytu. Podczas opracowywania bionicznej, dwupalcowej, zrobotyzowanej ręki, jeśli znane są średnice potencjalnych obiektów docelowych, odpowiednia długość kciuka i palca wskazującego może być wyznaczona na podstawie równania 2. W związku z tym, dwa modele regresji nieliniowej okazały się przydatne w projektowaniu optymalnych rozmiarów robotycznej ręki, której celem jest odtworzenie zdolności chwytnej kciuka i palca wskazującego. Podczas manipulowania nowym obiektem, sensoryczne sprzężenie zwrotne dostarcza nam informacji o jego fizycznych właściwościach, takich jak masa, a następnie mózg wybiera najbardziej odpowiedni model utrzymywany w naszym centralnym systemie nerwowym dla bieżącego zadania (Lemon et al., 1995; Davidson i Wolpert, 2004). Na podstawie zestawu maksymalnej masy chwytającej kciuka i palca wskazującego można opracować algorytm głębokiego uczenia, aby uzasadnić, czy niektóre obiekty w nieuporządkowanym środowisku pracy spełniają wymagania dotyczące chwytania dla bionicznych robotycznych dłoni. Ponadto, jeśli w nieuporządkowanym środowisku pracy znajdują się pewne nieregularne obiekty (np. kubek), zbiór maksymalnej średnicy chwytania palca wskazującego kciuka może zostać wykorzystany do stworzenia algorytmów planowania chwytania w celu wybrania optymalnych miejsc chwytania na nieregularnej powierzchni obiektu przez bioniczno-robotyczną rękę. Dodatkowo, wiele zmiennych w czasie problemów zawsze istnieje w problemach kontroli kinematycznej palców robotycznych, a zmiennoparametrowa zbieżna różnicowa sieć neuronowa byłaby wydajną i dokładną metodą rozwiązywania tego problemu planowania chwytania (Zhang i in., 2018a, b).
Wniosek
W tym badaniu zbadano maksymalną kooperacyjną masę chwytającą i średnicę ludzkiego kciuka i palca wskazującego w szerokim zakresie nieustrukturyzowanych zadań. Wiek uczestników wahał się od 3∼27 lat, a suma długości ich kciuka i palca wskazującego wynosiła od 56,9 do 132,6 mm. Wyniki badań wykazały, że maksymalne masy chwytne i średnice palca wskazującego i kciuka uczestników wynosiły od 690,2 do 9859,6 g oraz od 70 do 170 mm. Maksymalna masa chwytna palca wskazującego uczestników zależała od płci, wieku i sumy długości palców kciuka i wskaziciela (P < 0,05), ale nie od używanej ręki i stosunku długości palca wskazującego do kciuka (P > 0,05). Maksymalna średnica chwytna palca wskazującego uczestników zależała od wieku, sumy długości palców kciuka i stosunku długości palca wskazującego do długości kciuka (P < 0,05), ale nie od płci i używanej ręki (P > 0,05).
Istniał nieliniowy model regresji dla zależności maksymalnej masy chwytającej od płci, wieku i sumy długości palca wskazującego kciuka oraz inny nieliniowy model regresji dla zależności maksymalnej średnicy chwytającej od wieku, sumy długości palca wskazującego kciuka i stosunku długości palca wskazującego do długości kciuka. Dwa modele regresji okazały się przydatne w projektowaniu optymalnych rozmiarów robotycznych rąk, mających na celu odtworzenie zdolności chwytnej kciuka i palca wskazującego. Badania te mogą pomóc w określeniu nie tylko rozsądnej masy i rozmiaru chwytu dla bionicznej, zrobotyzowanej ręki, ale także wymagań dotyczących rehabilitacji ręki.
Oświadczenie o dostępności danych
Wszystkie zestawy danych wygenerowane w tym badaniu są zawarte w artykule/materiale uzupełniającym.
Wkład autorów
XC i ZL zaprojektowali i wykonali eksperymenty oraz napisali manuskrypt. YW, JL, i DZ przejrzeli i nadzorowali pracę.
Funding
Ta praca była wspierana przez European Marie Curie International Incoming Fellowship (326847 i 912847), Special Foundation for Talents of Northwest A&F University (Z111021801), Shaanxi Project of Science and Technology Activities for Returning from Overseas (2018030) oraz Key Research and Development Plan of Shaanxi Province (2019NY-172).
Konflikt interesów
Autorzy deklarują, że badania zostały przeprowadzone przy braku jakichkolwiek komercyjnych lub finansowych relacji, które mogłyby być interpretowane jako potencjalny konflikt interesów.
Abdel-Malek, A. K., Ahmed, A. M., El Sharkawi, S. A., and El Hamid, N. A. (1990). Przewidywanie wzrostu na podstawie pomiarów dłoni. Forensic Sci. Int. 46, 181-187. doi: 10.1016/0379-0738(90)90304-h
PubMed Abstract | CrossRef Full Text | Google Scholar
Bac, W., Hemming, J., Barth, R., and Wais, E. (2017). Ocena wydajności robota zbierającego słodką paprykę. J. Field Robot. 34, 1123-1139. doi: 10.1002/rob.21709
CrossRef Full Text | Google Scholar
Bansode, D. G., Borse, L. J., and Yadav, R. D. (2014). Study of correlation between dominant hand’s grip strength and some physical factors in adult males and females. Int. J. Pharm. Res. Health Sci. 2, 316-323.
Google Scholar
Biegstraaten, M., Smeets, J. B. J., and Brenner, E. (2006). The relationship between force and movement when grasping an object with a precision grip. Exp. Brain Res. 171, 347-357. doi: 10.1007/s00221-005-0271-z
PubMed Abstract | CrossRef Full Text | Google Scholar
Chen, X., Li, Z., Wang, Y., and Liu, J. (2019). Wpływ cech owoców i dłoni na stabilność siłowego chwytu kciuka-palca wskazującego podczas ręcznego sortowania owoców. Comput. Electron. Agric. 157, 479-487. doi: 10.1016/j.compag.2019.01.032
CrossRef Full Text | Google Scholar
Davidson, P. R., and Wolpert, D. M. (2004). Internal models underlying grasp can be additively combined. Exp. Brain Res. 155, 334-340. doi: 10.1007/s00221-003-1730-z
PubMed Abstract | CrossRef Full Text | Google Scholar
Eksioglu, M. (2004). Względna optymalna rozpiętość chwytu jako funkcja antropometrii ręki. Int. J. Ind. Ergonom. 34, 1-12. doi: 10.1016/j.ergon.2004.01.007
CrossRef Full Text | Google Scholar
Feix, T., Bullock, I., and Dollar, A. M. (2014). Analiza ludzkiego zachowania podczas chwytania: charakterystyka obiektu i rodzaj chwytu. IEEE Trans. Haptics 7, 311-323. doi: 10.1109/TOH.2014.2326871
PubMed Abstract | CrossRef Full Text | Google Scholar
Ishak, N. I., Hemy, N., and Franklin, D. (2012). Estimation of sex from hand and handprint dimensions in a Western Australian population. Forensic Sci. Int. 221, 154.e1-154.e6. doi: 10.1016/j.forsciint.2012.04.017
PubMed Abstract | CrossRef Full Text | Google Scholar
Jee, S. C., Bahn, S., and Yun, M. H. (2015). Określanie płci na podstawie różnych wymiarów dłoni Koreańczyków. Forensic Sci. Int. 257, 521.e1-521.e10. doi: 10.1016/j.forsciint.2015.10.014
PubMed Abstract | CrossRef Full Text | Google Scholar
Kanchan, T., and Krishan, K. (2011). Antropometria dłoni w określaniu płci rozczłonkowanych szczątków – przegląd literatury. J. Forensic Leg. Med. 18, 14-17. doi: 10.1016/j.jflm.2010.11.013
PubMed Abstract | CrossRef Full Text | Google Scholar
Lemon, R. N., Johansson, R. S., and Westling, G. (1995). Corticospinal control during reach, grasp, and precision lift in man. J. Neurosci. 15, 6145-6156. doi: 10.1523/jneurosci.15-09-06145.1995
PubMed Abstract | CrossRef Full Text | Google Scholar
Lexell, J., Sjostrom, M., Nordlund, A. S., and Taylor, C. C. (1992). Wzrost i rozwój ludzkich mięśni: ilościowe badanie morfologiczne całego vastus lateralis od dzieciństwa do wieku dorosłego. Muscle Nerve 15, 404-409. doi: 10.1002/mus.880150323
PubMed Abstract | CrossRef Full Text | Google Scholar
Li, K., Hewson, D. J., Duchene, J., and Hogrel, J. Y. (2010). Predicting maximal grip strength using hand circumference. Man. Ther. 15, 579-585. doi: 10.1016/j.math.2010.06.010
PubMed Abstract | CrossRef Full Text | Google Scholar
Li, Z., Li, P., Yang, H., and Wang, Y. (2013). Badania stabilności dwupalcowego chwytania pomidorów dla robotów zbierających. Biosyst. Eng. 116, 163-170. doi: 10.1016/j.biosystemseng.2013.07.017
CrossRef Full Text | Google Scholar
Li, Z., Miao, F., Yang, Z., Chai, P., and Yang, S. (2019a). Czynniki wpływające na rodzaj chwytu ludzkiej ręki w zbieraniu owoców pomidora: badanie statystyczne dla ergonomicznego rozwoju robota zbierającego. Comput. Electron. Agric. 157, 90-97. doi: 10.1016/j.compag.2018.12.047
CrossRef Full Text | Google Scholar
Li, Z., Miao, F., Yang, Z., and Wang, H. (2019b). Badanie antropometryczne dla antropomorficznego projektowania robotów zbierających pomidory. Comput. Electron. Agric. 163:104881. doi: 10.1016/j.compag.2019.104881
CrossRef Full Text | Google Scholar
Luciw, M. D., Jarocka, E., and Edin, B. B. (2014). Multi-channel eeg recordings during 3936 grasp and lift trials with varying weight and friction. Sci. Data 1:140047. doi: 10.1038/sdata.2014.47
PubMed Abstract | CrossRef Full Text | Google Scholar
Puh, U. (2009). Age-related and sex-related differences in hand and pinch grip stength in adults. Int. J. Rehabil. Res. 33, 4-11. doi: 10.1097/MRR.0b013e328325a8ba
PubMed Abstract | CrossRef Full Text | Google Scholar
Seo, N. J., and Armstrong, T. (2008). Badanie siły uchwytu, siły normalnej, powierzchni styku, rozmiaru dłoni i rozmiaru uchwytu dla uchwytów cylindrycznych. Hum. Factors 50, 734-744. doi: 10.1518/001872008×354192
PubMed Abstract | CrossRef Full Text | Google Scholar
Shurrab, M., Mandahawi, N., and Sarder, M. D. (2017). The assessment of a two-handed pinch force: quantifying different anthropometric pinch grasp patterns for males and females. Int. J. Ind. Ergon. 58, 38-46. doi: 10.1016/j.ergon.2017.02.006
CrossRef Full Text | Google Scholar
Silwal, A., Davidson, J. R., Karkee, M., and Mo, C. (2017). Design, integration, and field evaluation of a robotic apple harvester. J. Field Robot. 34, 1-18.
Google Scholar
Vigouroux, L., Domalain, M., and Berton, E. (2011). Effect of object width on muscle and joint forces during thumb-index finger grasping. J. Appl. Biomech. 27, 173-180. doi: 10.1123/jab.27.3.173
PubMed Abstract | CrossRef Full Text | Google Scholar
Wang, W., and Ahn, S. H. (2017). Shape memory alloy-based soft gripper with variable stiffness for compliant and effective grasping. Soft Robot. 4, 379-389. doi: 10.1089/soro.2016.0081
PubMed Abstract | CrossRef Full Text | Google Scholar
Yussof, H., and Ohka, M. (2012). Strategia chwytania i algorytm sterowania dwoma robotycznymi palcami wyposażonymi w optyczne trójosiowe czujniki dotykowe. Procedia Eng. 41, 1573-1579. doi: 10.1016/j.proeng.2012.07.352
CrossRef Full Text | Google Scholar
Zhang, Z., Fu, T., Yan, Z., Jin, L., Xiao, L., Sun, Y., et al. (2018a). A varying-parameter convergent-differential neural network for solving joint-angular-drift problems of redundant robot manipulators. IEEE ASME Trans. Mech. 23, 679-689. doi: 10.1109/tmech.2018.2799724
CrossRef Full Text | Google Scholar
Zhang, Z., Lu, Y., Zheng, L., Li, S., Yu, Z., and Li, Y. (2018b). A new varying-parameter convergent-differential neural-network for solving time-varying convex QP problem constrained by linear-equality. IEEE Trans. Automat. Contr. 63, 4110-4125. doi: 10.1109/tac.2018.2810039
CrossRef Full Text | Google Scholar
.