DOWNLOAD Mathematica Notebook
Grupa abelianów to grupa, dla której elementy są komutowalne (tzn. 
dla wszystkich elementów 
i 
). Grupy abelowskie odpowiadają zatem grupom o symetrycznej tabliczce mnożenia.
Wszystkie grupy cykliczne są grupami abelowskimi, ale grupa abelowska niekoniecznie jest cykliczna. Wszystkie podgrupy grupy abelowskiej są normalne. W grupie abelowskiej każdy element jest sam w klasie koniugacji, a tablica znaków obejmuje potęgi pojedynczego elementu znanego jako generator grupy.
W języku Wolframa funkcja AbelianGroup reprezentuje bezpośredni produkt grup cyklicznych stopni 
, 
, ….
Nie jest znana żadna ogólna formuła podająca liczbę nieizomorficznych grup skończonych danego rzędu grupy. Jednak liczba nieizomorficznych abelowskich grup skończonych 
dowolnego danego rzędu grup 
jest dana przez zapis 
jako
 |
(1)
|
gdzie 
są odrębnymi czynnikami pierwszymi, wtedy
 |
(2)
|
gdzie 
jest funkcją podziału, która jest zaimplementowana w języku Wolframa jako FiniteAbelianGroupCount. Wartości 
dla 
, 2, … wynoszą 1, 1, 1, 1, 2, 1, 1, 1, 3, 2, … (OEIS A000688).
Najmniejsze rzędy, dla których istnieją 
, 2, 3, … nieizomorficzne grupy abelowskie to 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), gdzie 0 oznacza niemożliwą liczbę (tzn. nie będącą iloczynem liczb partycji) nieizomorficznych grup abelowskich. Brakujące” wartości to 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Przyrostowo największe liczby grup abelowskich w funkcji rzędu są następujące: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), które występują dla rzędów 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).
Twierdzenie o dekompozycji Kroneckera mówi, że każda skończona grupa abelianów może być zapisana jako bezpośredni iloczyn grup cyklicznych rzędu grupowego o potędze pierwszej. Jeśli rząd grupy skończonej jest liczbą pierwszą 
, to istnieje jedna grupa abelianowska rzędu 
(oznaczana 
) i nie ma grup nieabelianckich. Jeśli rząd grupy jest podniesiony do kwadratu 
, to istnieją dwie grupy abelowskie (oznaczane 
i 
. Jeśli rząd grupy jest pierwiastkiem sześciennym 
, to istnieją trzy grupy abelianowe (oznaczone 
, 
i 
), a w sumie pięć grup. Jeśli porządek jest iloczynem dwóch liczb pierwszych 
i 
, to istnieje dokładnie jedna grupa abelianowa rzędu grupowego 
(oznaczana 
).
Innym ciekawym wynikiem jest to, że jeśli 
oznacza liczbę nieizomorficznych grup abelowskich rzędu grupowego 
, to
 |
(3)
|
gdzie 
jest funkcją zeta Riemanna.
Liczby grup abelowskich rzędu 
są dane przez 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, …. (OEIS A063966) dla 
, 2, …. Srinivasan (1973) pokazał też, że
 |
(4)
|
gdzie
 |
 |
 |
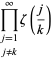(5)
|
 |
 |
 |
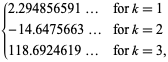(6)
|
(OEIS A021002, A084892, and A084893) and 
is again the Riemann zeta function. Zauważmy, że Richert (1952) błędnie podał 
. Sumy 
można też zapisać w postaci jawnej
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
 |
 |
 |
(9)
|
DeKoninck i Ivic (1980) pokazali, że
 |
(10)
|
gdzie
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
(OEIS A084911) jest iloczynem nad liczbami pierwszymi 
, a 
jest ponownie funkcją podziału.
Granice na liczbę nieizomorficznych grup nieabeliańskich są podane przez Neumanna (1969) i Pybera (1993).
Istnieje wiele dowcipów matematycznych z udziałem grup abelowskich (Renteln i Dundes 2005):
Q: Co jest fioletowe i komutowalne? O: Abeliańskie winogrono.
Q: Co jest lawendowe i komutuje? A: Abelian semigrape.
Q: Co jest fioletowe, dojeżdża i jest czczone przez ograniczoną liczbę ludzi? A: Skończenie czczone abelowskie winogrono.
Q: Co jest pożywne i dojeżdża do celu? O: Zupa abelianowa.