Zaczęliśmy od Konwolucji 2D w pierwszym poście, ponieważ konwolucje zyskały znaczną popularność po sukcesach w dziedzinie Widzenia Komputerowego. Ponieważ zadania w tej dziedzinie wykorzystują obrazy jako dane wejściowe, a naturalne obrazy zazwyczaj mają wzory wzdłuż dwóch wymiarów przestrzennych (wysokości i szerokości), częściej można zobaczyć przykłady Konwolucji 2D niż Konwolucji 1D i 3D.
Ostatnio jednak, nastąpiła ogromna liczba sukcesów w stosowaniu konwolucji do zadań przetwarzania języka naturalnego. Ponieważ zadania w tej dziedzinie wykorzystują tekst jako dane wejściowe, a tekst ma wzorce wzdłuż jednego wymiaru przestrzennego (tj. czasu), konwolucje 1D świetnie pasują! Możemy je wykorzystać jako bardziej wydajne alternatywy dla tradycyjnych rekurencyjnych sieci neuronowych (RNN), takich jak LSTM czy GRU. W przeciwieństwie do RNN, mogą one być uruchamiane równolegle dla naprawdę szybkich obliczeń.
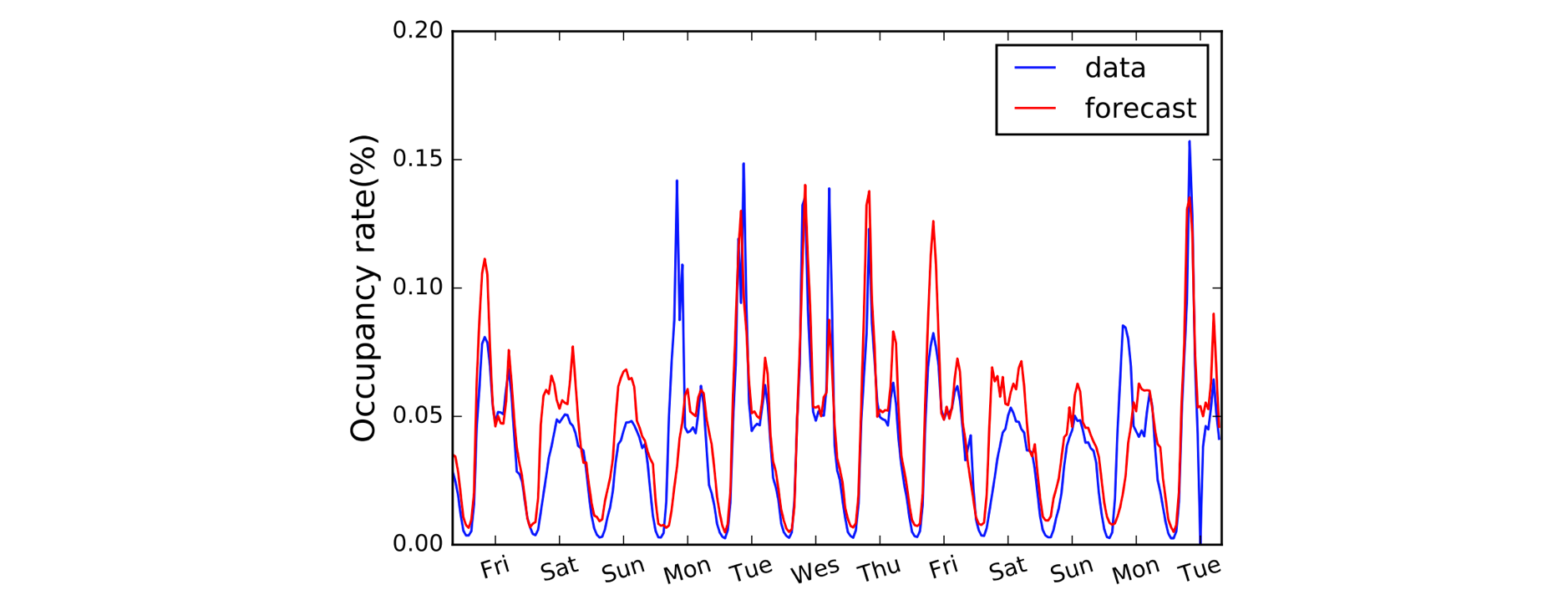
Inną dziedziną, która korzysta z 1D Convolutions jest modelowanie szeregów czasowych. Tak jak poprzednio, mamy pojedynczy wymiar przestrzenny na naszych danych wejściowych (tj. czas) i chcemy wyłapać wzorce w okresach czasu. Często nazywamy ten typ danych „sekwencyjnymi”, ponieważ mogą być one postrzegane jako sekwencja wartości. A wymiar przestrzenny często nazywamy wymiarem „czasowym”. Używanie 1D Convolutions przed RNNs jest również dość powszechne: model LSTNet jest tego przykładem, a jego przewidywania dla prognozowania ruchu drogowego są pokazane poniżej.
A, B, C. To proste jak (1,3,3) kropka (2,0,1) = 5.
Po wyjaśnieniu konwencji nazewnictwa przyjrzyjmy się teraz bliżej arytmetyce. Mamy szczęście, ponieważ konwolucje 1D są w rzeczywistości tylko uproszczoną wersją konwolucji 2D!

Pracując nad obliczaniem pojedynczej wartości wyjściowej, możemy zastosować nasze jądro o rozmiarze 3 do regionu o równoważnym rozmiarze po lewej stronie naszej macierzy wejściowej. Obliczamy 'iloczyn kropkowy’ regionu wejściowego i jądra, co w skrócie jest po prostu iloczynem pierwiastków (tj. mnożymy pary kolorów), po którym następuje globalna suma, aby uzyskać pojedynczą wartość. Tak więc w tym przypadku:
(1*2) + (3*0) + (3*1) = 5
Zastosujemy tę samą operację (z tym samym jądrem) do innych regionów tablicy wejściowej, aby otrzymać kompletną tablicę wyjściową (5,6,7,2); tzn. przesuwamy jądro przez całą tablicę wejściową. W przeciwieństwie do Konwolucji 2D, gdzie przesuwamy jądro w dwóch kierunkach, w przypadku Konwolucji 1D przesuwamy jądro tylko w jednym kierunku; lewo/prawo na tym diagramie.
Zaawansowane: Konwolucja 1D to nie to samo co Konwolucja 2D 1×1.
Kodowanie rzeczy w górę
Niespodziewanie, będziemy potrzebować bloku Conv1D w Gluonie dla naszej Konwolucji 1D. Zdefiniujemy kształt jądra jako 3, a ponieważ w tym przykładzie pracujemy tylko z pojedynczym jądrem, określimy channels=1.
import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)
Możemy teraz przekazać nasze dane wejściowe do bloku conv przy użyciu predefiniowanego jądra.
input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>
Co się zmienia dzięki paddingowi, rozstępowi i dylatacji?
Widzieliśmy efekt paddingu, rozstępu i dylatacji w ostatnim poście na temat konwolucji 2D, i jest on bardzo podobny dla konwolucji 1D. W przypadku paddingu, tym razem padamy tylko wzdłuż jednego wymiaru (wymiaru czasowego). Nasz diagram reprezentuje czas na osi poziomej, więc wypełniamy go po lewej i prawej stronie danych wejściowych (a nie powyżej i poniżej, jak w przykładzie 2D Convolution). W przypadku rozciągnięcia i dylatacji, stosujemy je również tylko wzdłuż wymiaru czasowego. Tak więc przykład z wypełnieniem i rozstępem wyglądałby następująco:

W kodzie dodajemy dwa dodatkowe argumenty: padding=1 i strides=2.
conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>
Zaawansowane: wymiary danych wejściowych muszą być zgodne z określonym porządkiem zwanym układem. Domyślnie konwolucja 1D oczekuje zastosowania do danych wejściowych w formacie 'NCW’, tj. rozmiar partii (N) * kanały (C) * szerokość/czas (W). A dla konwolucji 2D domyślnie jest NCHW, czyli wielkość partii (N) * kanały (C) * wysokość (H) * szerokość (W). Sprawdź argument
layoutwConv1DiConv2D.
.