Przedziały tolerancji
Ta sekcja zawiera szczegóły statystyczne dla jednostronnych i dwustronnych przedziałów tolerancji.
Przedziały oparte na rozkładzie normalnym
Przedział jednostronny
Przedział jednostronny jest obliczany w następujący sposób:
Lower Limit = 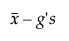
Upper Limit = 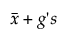
gdzie
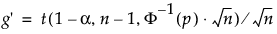
s jest odchyleniem standardowym
t jest kwantylem z niecentralnego rozkładu t
Φ-1 jest kwantylem normalnym
Obustronny przedział
Obustronny przedział jest obliczany w następujący sposób:
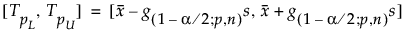
gdzie s jest odchyleniem standardowym, a g(1-α/2; p,n) jest stałą.
Aby określić g, należy rozważyć ułamek populacji uchwycony przez przedział tolerancji. Tamhane i Dunlop (2000) podają tę frakcję w następujący sposób:
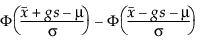
gdzie Φ oznacza standardową normalną cdf (funkcję rozkładu kumulatywnego).
Więc, g rozwiązuje następujące równanie:
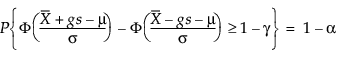
gdzie 1 – γ jest ułamkiem wszystkich przyszłych obserwacji zawartych w przedziale tolerancji.
Więcej informacji na temat przedziałów tolerancji opartych na rozkładzie normalnym można znaleźć w tabelach J.1a, J.1b, J.6a, i J.6b z Meeker et al. (2017).
Interwały nieparametryczne
Jednostronna dolna granica
Dolna 100(1 – α)% jednostronna granica tolerancji, która ma zawierać co najmniej część β przykładowego rozkładu z próby o rozmiarze n, to statystyka porządkowa x(l). Indeks l oblicza się w następujący sposób:
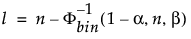
gdzie Φ-1bin(1-α, n, β) jest (1 – α)kwantylem trzeciego kwantyla rozkładu dwumianowego z n próbami i prawdopodobieństwem sukcesu β.
Prawdziwy poziom ufności jest obliczany jako Φbin(n-l, n, β), gdzie Φbin(x, n, β) jest prawdopodobieństwem tego, że zmienna losowa o rozkładzie dwumianowym z n próbami i prawdopodobieństwem sukcesu β jest mniejsza lub równa x.
Zauważmy, że aby obliczyć dolny jednostronnie wolny od rozkładu przedział tolerancji, wielkość próby n musi być co najmniej tak duża jak 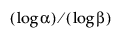 .
.
Jednostronna górna granica
Górna 100(1 – α)% jednostronna granica tolerancji zawierająca co najmniej część β rozkładu z próby o wielkości n jest statystyką porządkową x(u). Indeks u oblicza się w następujący sposób:
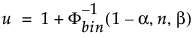
gdzie Φ-1bin(1-α, n, β) jest (1 – α)kwantylem trzeciego kwantyla rozkładu dwumianowego z n próbami i prawdopodobieństwem sukcesu β.
Prawdziwy poziom ufności jest obliczany jako Φbin(u-1, n, β), gdzie Φbin(x, n, β) jest prawdopodobieństwem tego, że zmienna losowa o rozkładzie dwumianowym z n próbami i prawdopodobieństwem sukcesu β jest mniejsza lub równa x.
Zauważ, że aby obliczyć górny jednostronny przedział tolerancji wolny od rozkładu, wielkość próby n musi być co najmniej tak duża jak 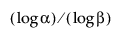 .
.
Dwustronny przedział tolerancji
Dwustronny przedział tolerancji 100(1 – α)% zawierający co najmniej część β rozkładu z próbki o rozmiarze n oblicza się w następujący sposób:
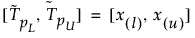
gdzie x(i) jest statystyką i-tego rzędu, a l i u są obliczane w następujący sposób:
Let ν = n – Φ-1bin(1-α, n, β), gdzie Φ-1bin(1-α, n, β) jest (1 – α)kwantylem rozkładu dwumianowego z n próbami i prawdopodobieństwem sukcesu β. Jeżeli ν jest mniejsze niż 2, nie można obliczyć przedziału tolerancji wolnego od rozkładu dwustronnego. Jeśli ν jest większe lub równe 2, l = floor(ν/2) i u = floor(n + 1 – ν/2).
Prawdziwy poziom ufności jest obliczany jako Φbin(u-l-1, n, β), gdzie Φbin(x, n, β) jest prawdopodobieństwem tego, że zmienna losowa o rozkładzie dwumianowym z n próbami i prawdopodobieństwem sukcesu β jest mniejsza lub równa x.
Zauważ, że aby obliczyć obustronnie wolny od rozkładu przedział tolerancji, wielkość próby n musi być co najmniej tak duża jak n w następującym równaniu:

Więcej informacji o wolnych od rozkładu przedziałach tolerancji, patrz Meeker et al. (2017, sekcja 5.3).