Rekonstrukcja 3D

W tym ćwiczeniu, intencją jest zaprogramowanie niezbędnej logiki pozwalającej robotowi kobuki na wygenerowanie rekonstrukcji 3D sceny, którą odbiera przez swoją lewą i prawą kamerę.

Instalacja

Instalacja ogólnej infrastruktury Akademii Robotyki JdeRobot.

Jak uruchomić swoje rozwiązanie?

Nawiguj do katalogu 3d_reconstruction

cd exercises/3d_reconstruction

Uruchom Gazebo ze światem kobuki_3d_reconstruction poprzez komendę

roslaunch ./launch/3d_reconstruction_ros.launch

Następnie musisz wykonać aplikację akademicką, która będzie zawierała Twój kod:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Jak wykonać ćwiczenie?

Aby wykonać ćwiczenie, należy edytować plik MyAlgorithm.py i wstawić do niego swój kod, który rekonstruuje punkty 3d z dwóch widoków stereo.

Gdzie wstawić kod?

W pliku MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Interfejs programowania aplikacji

• self.getImage('left') – aby uzyskać lewy obraz
• self.getImage('right') – aby uzyskać prawy obraz
• self.point.PlotPoint(position, color) – aby wykreślić punkt w narzędziu 3d

Prowadzenie interfejsu GUI

Podstawa myszy: Przytrzymaj i przeciągnij, aby poruszać się po środowisku. Scroll to zoom in or out

Keyboard based: Klawisze strzałek do poruszania się po środowisku. Klawisze W i S do powiększania lub pomniejszania

Teoria

W wizji komputerowej i grafice komputerowej, rekonstrukcja 3D jest procesem określania profilu 3D obiektu, jak również znajomości współrzędnych 3D dowolnego punktu na tym profilu. Rekonstrukcja może być osiągnięta w następujący sposób:

• Sprzętowe: Podejście sprzętowe wymaga od nas wykorzystania sprzętu specyficznego dla danego zadania rekonstrukcji. Wykorzystanie światła strukturalnego, dalmierza laserowego, głębokościomierza i metod radiometrycznych to tylko niektóre przykłady.

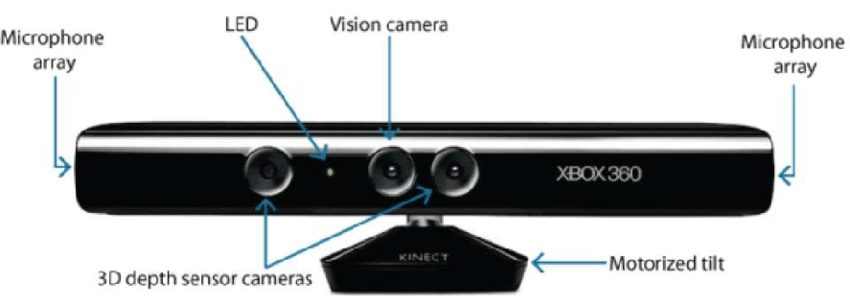
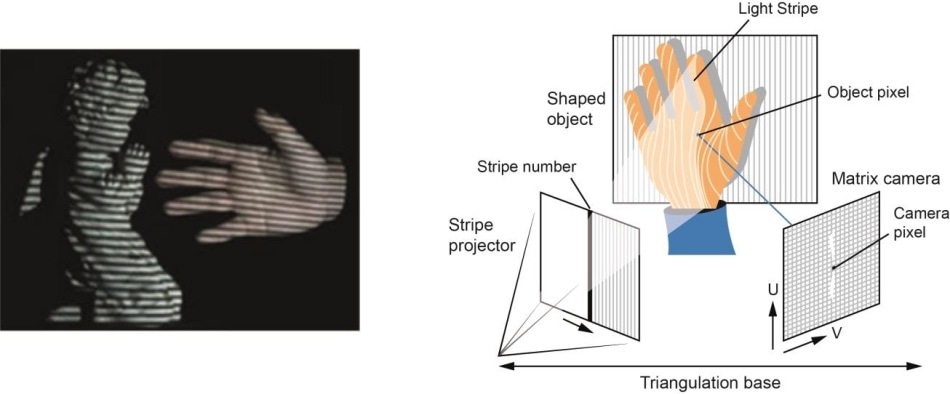
• Software Based: Podejście oparte na oprogramowaniu opiera się na możliwościach obliczeniowych komputera w celu określenia właściwości 3D obiektu. Kształt z cieniowania, tekstury, stereowizji i homografii są niektórymi dobrymi metodami.

W tym ćwiczeniu naszym głównym celem jest przeprowadzenie rekonstrukcji 3d przy użyciu podejścia opartego na oprogramowaniu, w szczególności rekonstrukcji 3d opartej na stereowizji.

Epipolar Geometry

Gdy dwie kamery oglądają scenę 3D z dwóch różnych pozycji, istnieje szereg relacji geometrycznych pomiędzy punktami 3D i ich rzutami na obrazy 2D, które prowadzą do ograniczeń pomiędzy punktami obrazu. Badanie tych właściwości i ograniczeń nazywane jest Geometrią Epipolarną. Poniższy obraz i wyjaśnienie może uogólnić ideę:

Załóżmy, że punkt X w przestrzeni 3d jest obrazowany w dwóch widokach, na x w pierwszym i x' w drugim. Rzutując wstecznie promienie na ich środki w kamerach przez płaszczyzny obrazu, otrzymujemy powierzchnię płaską, oznaczoną przez π.

Zakładając teraz, że znamy tylko punkt x, możemy zapytać, jak odpowiadający mu punkt x' jest ograniczony. Płaszczyzna π jest określona przez linię bazową (linię łączącą środki kamer) i półprostą zdefiniowaną przez x. Z powyższego wiemy, że półprosta odpowiadająca nieznanemu punktowi x' leży w π, stąd punkt x' leży na linii przecięcia l' π z drugą płaszczyzną obrazu. Linia ta nazywana jest linią epipolarną odpowiadającą punktowi x. Ta zależność pozwala nam zredukować przestrzeń poszukiwań punktu w prawym obrazie z płaszczyzny do prostej. Niektóre ważne definicje, na które należy zwrócić uwagę to:

• Epipol to punkt przecięcia linii łączącej środki kamer (linia bazowa) z płaszczyzną obrazu.

• Płaszczyzna epipolarna to płaszczyzna zawierająca linię bazową.

• Linia epipolarna jest punktem przecięcia płaszczyzny epipolarnej z płaszczyzną obrazu.

Rekonstrukcja tero

Rekonstrukcja tero jest szczególnym przypadkiem powyższej rekonstrukcji 3d, gdzie dwie płaszczyzny obrazu są równoległe do siebie i jednakowo odległe od punktu 3d, który chcemy wykreślić.

W tym przypadku linia epipolarna dla obu płaszczyzn obrazu jest taka sama i jest równoległa do szerokości płaszczyzn, upraszczając nasze ograniczenie lepiej.

Algorytm rekonstrukcji 3D

Algorytm rekonstrukcji składa się z 3 kroków:

1. Wykrywanie punktów charakterystycznych w jednej płaszczyźnie obrazu
2. Wykrywanie punktu charakterystycznego odpowiadającego punktowi znalezionemu powyżej
3. Triangulacja punktu w przestrzeni 3d

Przyjrzyjrzyjmy się im po kolei

Detekcja punktów charakterystycznych

Detekcja punktów charakterystycznych jest rozległym obszarem badań, w którym zbadano już kilka algorytmów. Harris Corner Detection i Shi-Tomasi algorytmy używają wartości własnych, aby uzyskać dobry punkt charakterystyczny. Ale problem polega na tym, że potrzebujemy wielu punktów do rekonstrukcji 3D, a te algorytmy nie będą w stanie dostarczyć nam tak dużej liczby punktów charakterystycznych.

W związku z tym, używamy punktów krawędziowych jako naszych punktów charakterystycznych. W kolejnym etapie algorytmu może pojawić się niejednoznaczność w ich wykrywaniu. Ale, nasz problem jest rozwiązany przez przyjęcie krawędzi jako punktów charakterystycznych. Jednym z naprawdę fajnych detektorów krawędzi jest algorytm Canny Edge Detection Algorithm. Algorytm ten jest dość prosty i niezawodny jeśli chodzi o generowanie krawędzi.

Wyciąganie punktów charakterystycznych

Użycie ograniczenia epipolarnego naprawdę upraszcza złożoność czasową naszego algorytmu. Dla ogólnych problemów rekonstrukcji 3d, musimy wygenerować linię epipolarną dla każdego punktu w jednej klatce obrazu, a następnie wyszukać w tej przestrzeni próbkowania odpowiadający mu punkt w drugiej klatce obrazu. Generowanie linii epipolarnej jest również bardzo proste w naszym przypadku, jest to po prostu iterpolacja równoległej linii z lewego obrazu do prawej płaszczyzny obrazu.

Sprawdzanie zgodności pomiędzy obrazami wymaga wielu algorytmów, takich jak Suma Różnic Kwadratowych czy Minimalizacja Energii. Nie zagłębiając się zbytnio, użycie prostego filtra korelacji również wystarczy w naszym przypadku.

Triangulacja

Triangulacja w prostych słowach jest po prostu obliczaniem, gdzie punkt 3d będzie leżał używając dwóch wyznaczonych punktów w płaszczyznach obrazu.

W rzeczywistości, pozycja punktów obrazu nie może być zmierzona dokładnie. Dla ogólnych kamer, może być geometryczne lub fizyczne zniekształcenia. Dlatego wiele matematyki idzie za minimalizacją tego błędu i obliczaniem najdokładniejszej projekcji punktu 3d. Odnieś się do tego linku dla prostego modelu.

Wskazówki

Proste wskazówki dostarczone, aby pomóc w rozwiązaniu ćwiczenia 3d_reconstruction. Biblioteka OpenCV jest szeroko wykorzystywana w tym ćwiczeniu.

Setup

Używając API ćwiczenia, możemy łatwo pobrać obrazy. Ponadto, po uzyskaniu obrazów, dobrym pomysłem jest wykonanie dwustronnego filtrowania na obrazach, ponieważ istnieją pewne dodatkowe szczegóły, które nie muszą być uwzględnione podczas rekonstrukcji 3d. Sprawdź ilustracje dla efektów wykonywania filtrowania dwustronnego.

Obliczanie korelacji

OpenCV ma już wbudowane filtry korelacji, które mogą być wywołane przez matchTemplate(). Zwróć uwagę na skrajne przypadki, takie jak krawędzie i narożniki.

Jedną z dobrych obserwacji jest to, że punkty po lewej stronie będą miały korespondencje w lewej części, a punkty po prawej stronie będą miały korespondencje w prawej części. Używając tego spostrzeżenia, możemy łatwo przyspieszyć obliczanie korespondencji.

Plotting the Points

Albo ręczne lub oparte na OpenCV funkcja triangulatePoints działa dobrze dla triangulacji. Wystarczy zadbać o wszystkie kształty i rozmiary macierzy podczas wykonywania implementacji algebraicznych.

Pamiętaj o różnicy między prostymi współrzędnymi 3D a jednorodnymi współrzędnymi 4D. Sprawdź ten film, aby uzyskać szczegółowe informacje. Po prostu podzielenie kompletnego wektora 4d przez jego 4 współrzędną daje nam współrzędne 3d.

Z powodu różnych implementacji użytkowników, użytkownik może być zmuszony do dostosowania skali i przesunięcia triangulowanych punktów, aby były one widoczne i reprezentowalne w interfejsie GUI. Dobrze sprawdza się zmniejszanie skali wektora współrzędnych 3D o wartość pomiędzy 500 a 1000. Również przesunięcie o wartość od 0 do 8 działa dobrze.

Ilustracje

.