Removal of power-line interference from the ECG: a review of the subtraction procedure

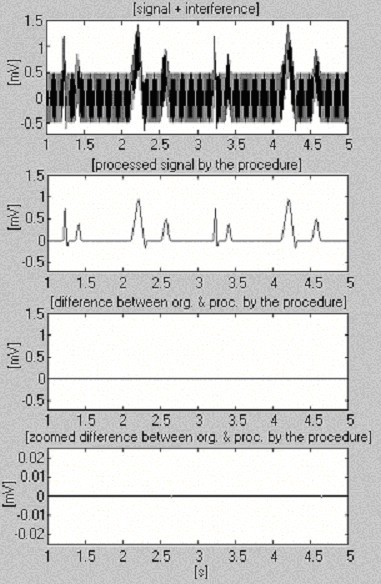
Jeden z pierwszych wyników uzyskanych za pomocą procedury odejmowania.

Kryterium liniowe

Kryterium liniowe, Cr, odpowiada zwykle drugiej różnicy sygnału (matematyczna ocena liniowości). Pierwsze Cr definiuje się w następujący sposób. Sześć kolejnych pierwszych różnic, FD i , jest obliczanych przy użyciu próbek sygnału, X i , oddalonych o jeden T PL :

FD i = X i+n – X i , dla i = 1 … 6 (1)

Zakłócenia PL w pierwszych różnicach są tłumione, jeżeli n = f S /f PL . W tym przypadku n = 5, ponieważ procedura została opracowana początkowo dla f PL = 50 Hz i f S = 250 Hz. Ponadto, maksymalne wartości FD max i minimalne FD min są brane do wyznaczenia Cr:

Cr = | FD max – FD min | <M, (2)

gdzie M jest wartością progową.

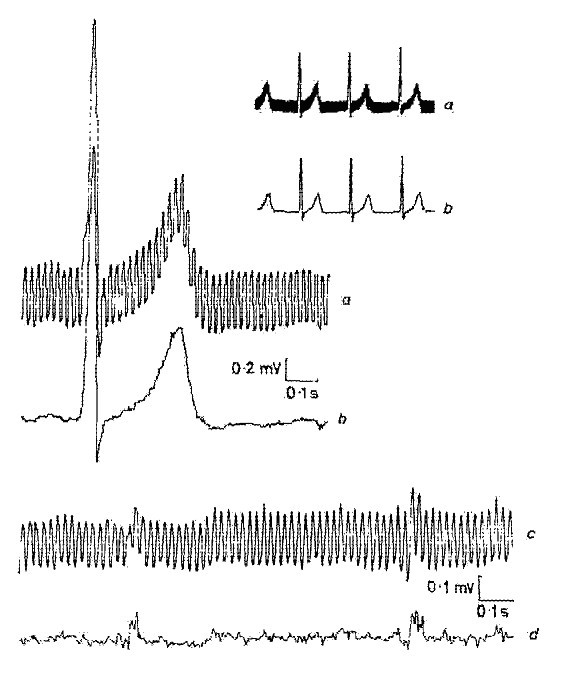
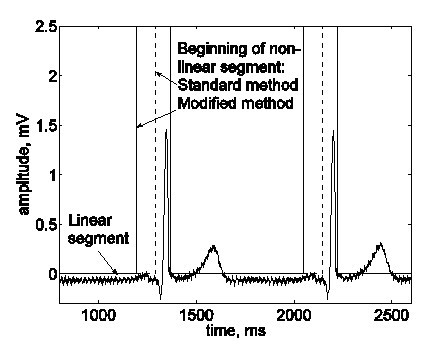
Typowe liniowe i nieliniowe segmenty są pokazane na Rys. 2. Na rzeczywisty sygnał EKG (ślad a) nałożone są zakłócenia (ślad b). Segmenty liniowe zawierają składowe o niskiej częstotliwości sygnału oraz składowe o częstotliwości linii zasilającej. Przybliżone widmo częstotliwościowe takich segmentów liniowych pokazano na Rys. 3.

Typowe segmenty liniowe i nieliniowe w rzeczywistym sygnale EKG.

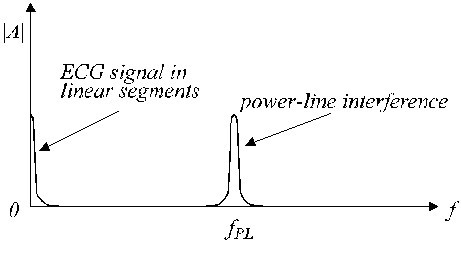
Przybliżone widmo częstotliwościowe segmentu liniowego.

Kryterium to działa dokładnie, ale trudno je zastosować w czasie rzeczywistym ze względu na stosunkowo powolną implementację. Ta wada została przezwyciężona przez Christova i Dotsinsky’ego, którzy używają zmodyfikowanego kryterium tylko dwóch kolejnych różnic.

Cr = | FDi+1- FD i | <M. (3)

Pierwsza próbka, która nie spełnia równania (3), jest związana z początkiem odcinka nieliniowego. W przejściu nieliniowym do liniowego, równanie (3) powinno być spełnione kolejno n razy, aby uniknąć przedwczesnego wykrycia segmentu liniowego. Kryterium zostało zaimplementowane w czasie rzeczywistym dla f S = 400 Hz i n = 8.

Później Dotsinsky i Daskalov zdefiniowali kryterium jako dwie nie następujące po sobie różnice:

Cr = |FDi+k- FD i | <M, dla k >1 (4)

Podejście to sprawia, że przejście z segmentu liniowego do nieliniowego jest bardziej precyzyjne.

Kompensacja zmian amplitudy PL

Im częściej aktualizowane są poprawki, tym lepszą kompensację zmian amplitudy PL uzyskuje się. Dlatego próg kryterium liniowego, M, musi być rozsądnie mniej restrykcyjny, tak aby błędy popełniane przez uśrednianie niektórych segmentów odbiegających od idealnego sygnału liniowego były mniejsze niż błędy, które pojawią się, jeśli M zainicjuje sporadyczną aktualizację korekcji. Początkowo M ustalono na 160 μV . Później stwierdzono, że heurystycznymi wartościami są M = 150 μV i M = 100 μV .

Filtrowanie liniowe

Dla nieparzystej liczby próbek n = 2m + 1 w jednym okresie zakłócenia PL, wartość filtrowana:

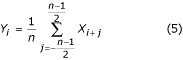
jest koincydencją fazową z wartością niefiltrowaną.

W przypadku parzystej liczby n = 2m, obie wartości są przesunięte w fazie o połowę okresu próby:

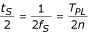
ale stają się zbieżne w fazie korzystając ze wzoru

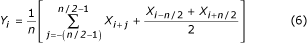
Możliwe jest przyjmowanie do uśredniania co drugiej, trzeciej lub q-tej próbki jeśli n/q jest liczbą całkowitą. W zależności od tego, czy n/q jest nieparzyste czy parzyste, stosuje się odpowiednio równanie (7) lub (8).

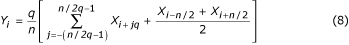
Szczególny przypadek maksymalnego skrócenia próbki występuje przy q = n/2 . Odpowiadający mu wzór:

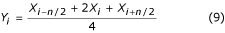
nazywany jest filtrem „trzypunktowym”. Oprócz równania (8) można również zastosować następujący wzór

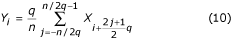
, jeśli q jest parzyste. W przypadku q = n/2, filtr staje się „dwupunktowy” i jest reprezentowany przez:

Zmniejszona liczba próbek w okresie zakłóceń doprowadzi do zwiększenia stromości zbocza płatów filtru grzebieniowego i skróci czas obliczeń. Jednak te „zalety” muszą być ostrożnie oceniane, aby nie naruszyć reguły Nyquista przy dużej ilości trzeciej harmonicznej. Inne harmoniczne nie są brane pod uwagę, ponieważ najwyższe nieparzyste harmoniczne są zwykle tłumione przez filtry dolnoprzepustowe z odcięciem w zakresie 100-150 Hz, podczas gdy parzyste są praktycznie nieobecne ze względu na precyzyjne wykonanie biegunów generatorów elektrowni.

Kompensacja zmian częstotliwości PL

Dopuszczalne odchylenie od częstotliwości znamionowej PL jest ograniczone w niektórych krajach do 1% przez normy. W praktyce odchylenia są często większe. Kumaravel et al. podali odchylenia rzędu 3%. McManus i wsp. stwierdzili znaczne zmiany w częstotliwości zakłóceń, która jest nakładana na zapisy pobrane z bazy danych Common Standards for Electrocardiography (CSE).

Zmiany częstotliwości prowadzą do szczególnego przypadku nie-wielokrotnego próbkowania z rzeczywistym n, zamiast całkowitego. Ta komplikacja może być ominięta, jeśli odchylenia są wykrywane przez ciągły sprzętowy pomiar f PL i korygowane przez małe korekty odstępu próbkowania t S wokół jego wartości znamionowej (R), t RS = T RPL /n (tutaj, T RPL = 20 ms jest znamionowym T PL dla f RPL = 50 Hz). Dla f PL , odchylenia pomiędzy 49,5 a 50,1 Hz, wahania t S są rzędu 1%, a co za tym idzie nie wprowadzają błędów wykraczających poza przyjętą dokładność pomiarową parametrów, które są zwykle stosowane do automatycznej klasyfikacji EKG.

Pierwsze podejście kojarzy wyzwalanie każdej pierwszej próbki, S 1 , z sekwencji S k (k = 1, 2…n) w okresach T PL z dowolnie wybraną, ale stałą amplitudą napięcia PL. Kolejne próbki, S k (k = 2…n), są oddalone od siebie o t S , co otrzymuje się przez t S = T RTL /n. Dla częstotliwości 50 Hz i n = 5, t S = 4 ms. Dwa rodzaje błędów popełnianych przy zastosowaniu tego podejścia są badane przez Dotsinsky’ego i Daskalova . Pierwszy z nich, wynikający z nieregularności międzypróbkowych, może sięgać 1% przy f S = 400 Hz i 1,2% przy f S = 250 Hz, w przypadku 1% odchylenia wokół f RPL . Drugi rodzaj błędu nie przekracza 3% i jest konsekwencją dodatkowo przesuniętej lokalizacji filtrowanej próbki.

Dotsinsky i Daskalov podali ulepszone podejście. Bieżący okres T PL jest mierzony i dzielony przez n. Otrzymany t S jest wykorzystywany w kolejnym T PL .

Ocena skuteczności procedury

Przykłady procedury subtrakcji przedstawiono na rys. 4 i rys. 5. Sygnały EKG pochodzą z bazy danych American Heart Association. Sygnały są filtrowane notchowo w celu wytłumienia zakłóceń o częstotliwości 60 Hz (częstotliwość PL w USA). Następnie sygnały są mieszane z zakłóceniami o częstotliwości 50 Hz, modulowane amplitudowo od 0 do 3,2 mVp-p z szybkością przesuwu 200 μVs-1. Ślady są identyfikowane w następujący sposób: i) sygnał wejściowy; ii) zsyntetyzowane zakłócenia; iii) sygnał mieszany; iv) sygnał przetworzony; v) różnica pomiędzy sygnałem oryginalnym i przetworzonym oraz vi) różnica powiększona. W rzeczywistości, odrzucane komponenty zawierają również szumy elektromiograficzne (EMG) i inne. Niestłumiona część sygnału, wraz z niewielkimi pozostałymi zakłóceniami i zniekształceniami wynikającymi z kompromisu z wartością M są również obecne w różnicach.

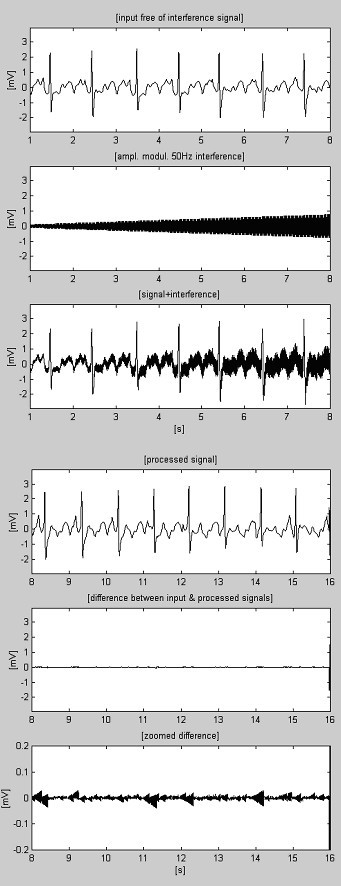
Przetworzony zapis AHA 3004d1.

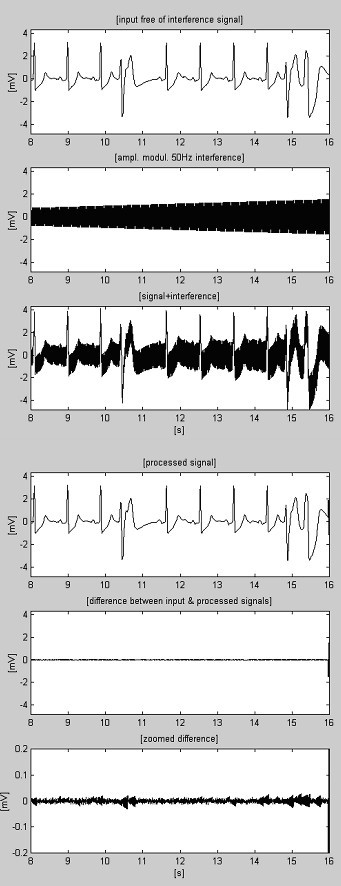
Przetworzone nagranie AHA 6007d1.

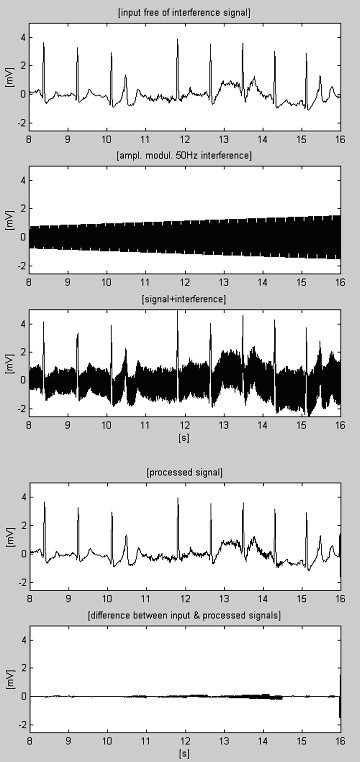
Dwa sygnały służą do oceny skuteczności procedury odejmowania tylko w odniesieniu do interferencji. Pierwszy, pobrany z własnej bazy danych, nazywamy warunkowo „czystym” (Rys. 6). Wynik pokazuje niewielkie różnice pomiędzy sygnałem wejściowym a przetworzonym, wizualnie spowodowane szumem prezentowanym na wejściu. Wynik ten jest weryfikowany z drugim zsyntetyzowanym sygnałem, który nie zawiera żadnych zakłóceń (Rys. 7). Jak można zauważyć, nie wprowadza on żadnych zniekształceń. Na ten sam zsyntetyzowany sygnał nałożono zakłócenia i poddano obróbce (Rys. 8). Nie można znaleźć żadnych resztek zakłóceń.

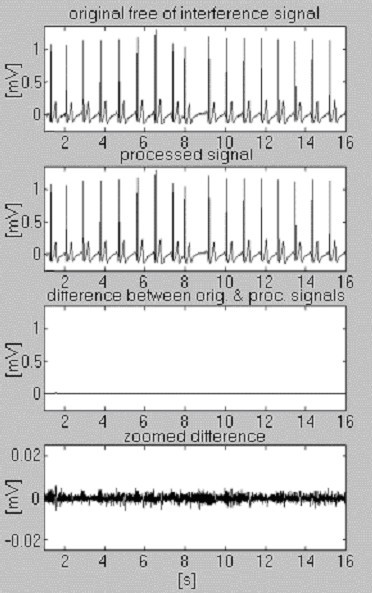
Przetwarzanie warunkowo „czystego” sygnału.

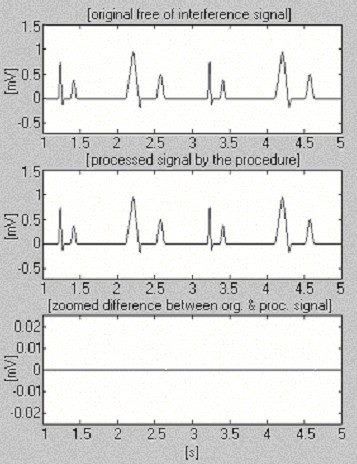
Przetwarzanie sygnału zsyntetyzowanego.

Przetwarzanie sygnału zsyntetyzowanego+zakłócenia.

Wpływ szumu EMG

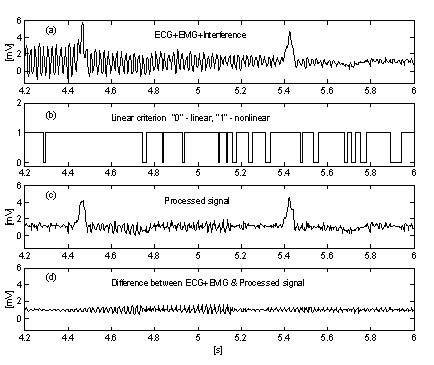
Niekiedy szum EMG jest tak duży, że utrudnia znalezienie segmentu liniowego. W konsekwencji niedokładne korekty, które nie odpowiadają ostatniej zmianie amplitudy zakłóceń, powodują błędy (patrz szum resztkowy między 11. a 14. s na ryc. 9).

Przetworzony sygnał EKG+szum EMG+zakłócenia.

Bardzo proste podejście do tłumienia wpływu szumu EMG na procedurę wprowadza dodatkowy równoległy bufor, w którym trwające porcje sygnału są bezwarunkowo uśredniane . Bufor ten jest wykorzystywany do dokładnej detekcji liniowości. Rys. 10 i Rys. 11 przedstawiają porównanie wyników bez i z buforem równoległym. Ślady 'a’ reprezentują sygnał EKG zmieszany z zakłóceniami i szumem EMG. Ślady 'b’ na Rys. 10 i 'c’ na Rys. 11 wskazują przejścia z segmentów liniowych do nieliniowych (funkcje on-off). Jak widać, uśredniona część sygnału na rys. 10 jest bardzo ograniczona. W konsekwencji zmniejsza się efektywność procedury (rys. 10c i 10d. Z kolei bufor równoległy pozwala na detekcję długich odcinków liniowych (rys. 11c, a szum resztkowy w przetwarzanym sygnale (rys. 11d jest niski. Jednak szum nie jest całkowicie wytłumiony, ponieważ jego część bierze udział w obliczeniach korekcyjnych.

Subtrakcja szumu interferencyjnego+EMG bez bufora równoległego.

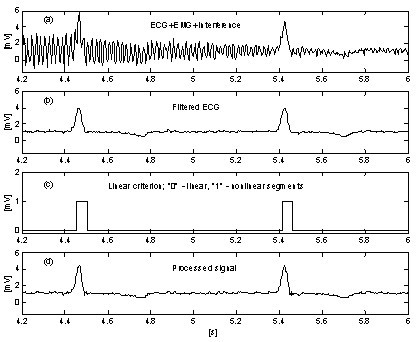
Subtrakcja zakłóceń+szumu EMG z buforem równoległym.

Dalszą poprawę tłumienia szumu EMG uzyskuje Christov poprzez zastosowanie adaptacyjnej wartości progowej M, która jest obliczana w odniesieniu do stosunku szumu do sygnału Rt, zdefiniowanego jako Rt = S NL /S F , gdzie poziom szumu S NL równa się sumarycznej szerokości nieliniowych segmentów w epoce S F , w przybliżeniu odpowiadającej rozważanemu interwałowi RR. Poszukiwanie liniowości przy kryterium M = 150 μV dla „czystego” EKG (Rys. 12a) oraz dla tego samego sygnału, ale zanieczyszczonego szumem EMG (Rys. 12b) wykazuje różne S NL , (Rys. 12c i 12d). Metoda została opracowana w środowisku MATLAB. Początkowy próg M jest wybierany jako równy 30 μV. Następnie jest on stopniowo zwiększany, aż do osiągnięcia przez Rt poziomu 10%, po czym uruchamiana jest procedura odejmowania. Wartość Rt ≤ 0,1 jest sugerowana przez stosunek szerokości zespołu QRS do jego odstępu RR, który zwykle wynosi około 10%. Eliminację zarówno zakłóceń, jak i szumu EMG można zaobserwować na ryc. 13b i 13d, gdzie zastosowano M = 420 μV. Dla porównania, „czysty” sygnał EKG jest przetwarzany z M = 35 μV (Rys. 13a i 13c).

Poziomy szumów SNL (ślady c i d) odpowiednio w „czystym” sygnale EKG (ślad a) i zanieczyszczonym sygnale EMG (ślad b).

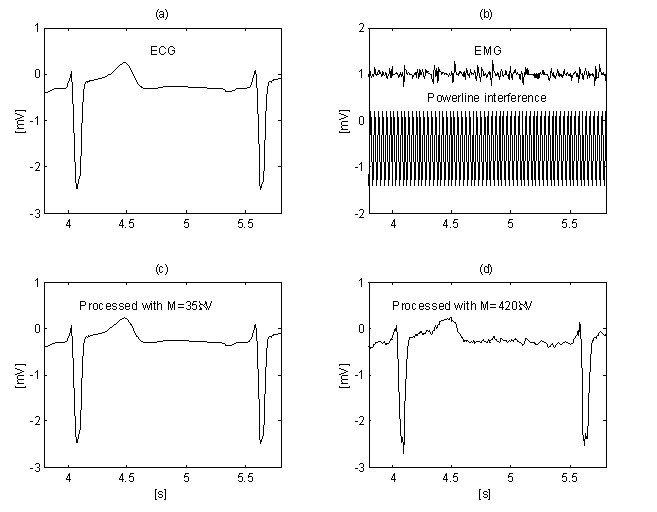
Tłumienie szumu zakłóceń+EMG przy użyciu adaptacyjnego progu M: „czysty sygnał” (a) przetworzony z M = 35 μV (c) i zanieczyszczony sygnał (b) poddany procedurze z M = 420 μV (d).

U pacjentów z migotaniem przedsionków i komór nie można regularnie znaleźć segmentów liniowych. Jednak całkowite zachowanie kształtu fali nie jest konieczne do wykrywania migotania i dlatego można stosować wszystkie rodzaje tradycyjnych filtrów.

Tłumienie zakłóceń w EKG wysokiej rozdzielczości

Procedura odejmowania nie ma bezpośredniego zastosowania do His-ECG powierzchni ciała, ponieważ fali His o niskiej amplitudzie i stosunkowo niskiej częstotliwości nie można wyróżnić w segmentach liniowych. Dlatego też fala Hisa będzie w praktyce tłumiona lub nawet usuwana z sygnału. Szum EMG ma zazwyczaj wyższą amplitudę i znacznie wyższą częstotliwość w porównaniu do powierzchniowej fali Hisa. Dlatego prosta zmiana wartości progowej, M, nie prowadzi do akceptowalnego rozgraniczenia segmentów liniowych i nieliniowych.

Bazhina i wsp. wprowadzili następującą modyfikację. Początek wykrywanego segmentu nieliniowego przed zespołem QRS jest przesuwany o 100 ms w lewo, co domyślnie definiuje region fali Hisa jako segment nieliniowy (ryc. 14).

Początek nieliniowego segmentu obejmującego zespół QRS został domyślnie przesunięty o 100 ms w lewo, aby objąć strefę, w której spodziewane jest pojawienie się fali pęczka Hisa.

Procedura odejmowania i trzy inne metody: filtry notch, interpolacja spektralna , i odejmowanie regresyjne są testowane przeciwko minimalnym zniekształceniom oryginalnego sygnału . Procedury odejmowania i odejmowania z regresją okazały się najlepsze, gdyż Baratta i in. stosują podobną koncepcję do estymacji szumu w segmentach liniowych. Regresja-subtrakcja słabo radzi sobie ze zmianami amplitudy zakłóceń w obrębie bieżącego segmentu.

Przypadek urządzeń zasilanych bateryjnie i komputerowych systemów wspomagania EKG

Sprzętowy pomiar f PL , niezbędny do kompensacji modulacji częstotliwości zakłóceń, nie jest możliwy do wykonania w urządzeniach zasilanych bateryjnie i w niektórych komputerowych systemach wspomagania EKG. Dotsinsky i Stoyanov badali zakres zmian częstotliwości zakłóceń o stałej amplitudzie, dla których część resztkowa jest ograniczona do akceptowalnego poziomu bez użycia zsynchronizowanego próbkowania. Stwierdzili, że zakłócenia resztkowe poniżej 20 μVp-p można uzyskać przy zastosowaniu procedury: i) amplituda zakłóceń ≤ 0,4 mVp-p oraz ii) zmiana częstotliwości z szybkością ≤ 0,0125 Hzs-1. Ponieważ takie wymagania dotyczące zasilania mogą być często przekraczane, opracowano programowy pomiar zakłóceń.

Sygnał EKG jest wstępnie przetwarzany przez filtr pasmowo-przepustowy o częstotliwości 49-51 Hz. Mierzone są amplitudy dwóch sąsiednich próbek, Br L i Br R , pobranych z dodatnio nachylonego zbocza interferencji, znajdujących się poniżej i powyżej linii zerowej (rys. 15). Odległość, t CP , między punktem przecięcia CP i prawą próbką, Br R , jest obliczana w sposób ciągły przez:

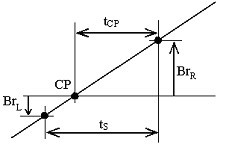
Przejście zerowe interferencji.

W przypadku zmiany T PL, t S jest redefiniowane przy użyciu

Podejście to zostało zaimplementowane w środowisku MATLAB. Dla częstotliwości próbkowania f S = 500 Hz i f RPL = 50 Hz, n jest równe 10. Iloczyn kn określa czas, jaki powinien upłynąć przed obliczeniem i podstawieniem nowego tCP,i + kn do poprzedniego tCP,i. Na rys. 16 przedstawiono przetworzony sygnał EKG o napięciu 1 mV po zmieszaniu z zakłóceniami o stałej amplitudzie 2 mVp-p i ekstremalnie szybkiej zmiennej o 1 Hz na 8 s częstotliwości (pierwszy ślad). Dla oceny uzyskanej efektywności przedstawiono również powiększoną różnicę bez synchronizowanego próbkowania (ostatni ślad).

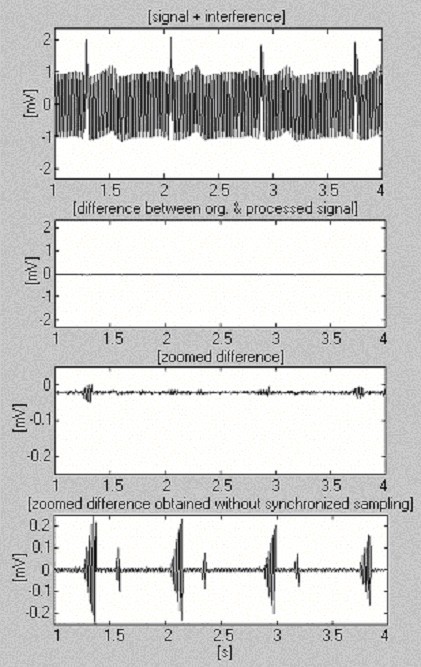
Procedura subtrakcji z wykorzystaniem programowego pomiaru częstotliwości linii zasilającej.

Kolejny logiczny krok, jaki należy wykonać, polega na: i) zachowaniu znamionowego t S aparatu EKG, ii) ponownym próbkowaniu sygnału zgodnie z mierzoną na bieżąco f PL w celu wyeliminowania zakłóceń i iii) powrocie do znamionowego t S . Pierwsze wyniki takiego podejścia są bardzo obiecujące. Tak więc, programowa kompensacja zmiennej f PL , jak również całkowita implementacja procedury odejmowania w przyrządzie, włączając w to automatyczną regulację dla f RPL 50 lub 60 Hz, zostanie zrealizowana niezależnie od obwodów sprzętowych i odpowiedniego oprogramowania.

Automatyczna adaptacja do znamionowej częstotliwości PL

Wspólny program do alternatywnego odejmowania zakłóceń w środowisku 50 i 60 Hz prowadzi do nie-wielokrotnego próbkowania, tj. do rzeczywistego n. Powszechnie stosowane wartości t S dla f RPL = 50 Hz, takie jak 250, 500 i 1000 Hz, odpowiadają irracjonalnym n z 4.1(6), 8.3(3) i 4.1(6), jeśli należy wyeliminować zakłócenia 60 Hz. W odwrotnym przypadku, f S = 360 Hz wymaga n = 7,2. Niedopuszczalne jest stosowanie zaokrąglonych wartości n*, ponieważ wprowadziłyby one znaczny błąd.

Bardzo proste rozwiązanie nie wymagające zmiany f S zostało znalezione przez Dotsinsky’ego i Stoyanova . Oryginalna procedura stosuje filtr grzebieniowy przez jeden okres, T PL , zakłócenia. Dzięki temu program działa szybciej. Ogólnie, n może być brane z k > 1 całych okresów. Procedura działa, jeżeli:

n = kT PL /t S jest liczbą całkowitą.

Dla t S = 2 ms (f S = 500 Hz) i f RPL = 50 Hz, najmniejszą wartością k spełniającą równanie (14) jest rzeczywiście k = 1. Natomiast w przypadku 60 Hz, k jest równe 3. Zera związane z subharmonikami 20 i 40 Hz też się pojawią, ale nie mają wpływu na procedurę. Dlatego wystarczy przełączyć n pomiędzy 10 (k = 1) i 25 (k = 3), aby móc pracować z obydwoma zakłóceniami. W tym celu dwa cyfrowe filtry pasmowo-przepustowe sprawdzają sygnał wejściowy. Na rys. 17 widać, że filtr o paśmie częstotliwości pokrywającym się z zakłóceniami generuje o rząd wielkości wyższy sygnał wyjściowy niż drugi filtr.

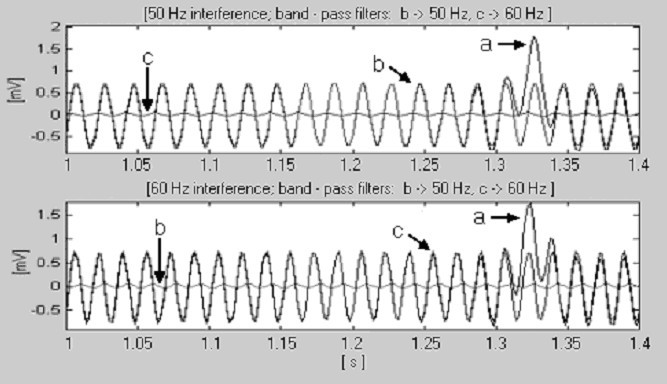
Detekcja znamionowej częstotliwości linii energetycznej, a) fragment zespołu QRS, b) zakłócenia 50 Hz i c) zakłócenia 60 Hz.

Rozwój procedury teoretycznej

Teoria procedury odejmowania była dalej rozwijana przez Mihova , Levkova i Mihova , oraz Mihova i in . Zaproponowali oni cztery typy filtrów, zaimplementowanych w uogólnionej strukturze, która może pokonać problemy z prawie wszystkimi przypadkami nie-wielokrotnego próbkowania, włączając w to zmiany częstotliwości zakłóceń, bez użycia zsynchronizowanej konwersji AD.

Tzw. filtr D w wielokrotnym próbkowaniu jest zdefiniowany jako Cr w równaniu (2), gdzie druga różnica, D i , jest otrzymywana z FD s, które są oddalone o jeden T PL :

D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)

Funkcja przenoszenia filtra D ma zera przy f = 0 i f = f PL Hz, która na rys. jest pokazana jako równa 50 Hz. 18.

Funkcja przenoszenia filtra D dla fPL = 50 Hz.

Filtr K opisuje średnią ruchomą przedstawioną równaniami (5) i (6). Jego funkcja przenoszenia podana jest na rys. 19 dla n = 5 w przypadku nieparzystej krotności.

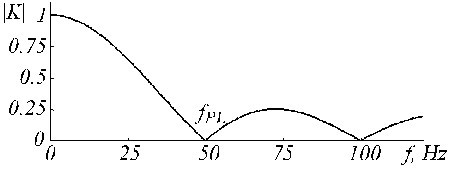
Funkcja przenoszenia filtra K dla fPL = 50 Hz i n = 5.

Równanie używane do bieżącego obliczania składowych zakłóceń:

B i = X i – Y i (16)

w rzeczywistości definiuje filtr cyfrowy zwany (1-K)-filtrem.

Ponadto, filtry są ponownie zdefiniowane dla próbkowania nie-wielokrotnego, a f S = 250 Hz w połączeniu z f RPL = 60 Hz jest brane pod uwagę w celu zilustrowania ulepszenia oprogramowania.

Aby zachować zera funkcji przenoszenia, filtr D musi być odjęty filtrem korekcyjnym z zerem przy f = 0 i wzmocnieniem D RPL przy f = f RPL , równym wzmocnieniu filtra D dla tej samej częstotliwości, f RPL . Synteza filtru korekcyjnego opiera się na trzypunktowym filtrze pomocniczym danym równaniem:

gdzie (n/2)* jest zaokrągloną wartością n/2.

Ponieważ A RPL jest wzmocnieniem filtru pomocniczego dla f = f RPL , filtr korekcyjny jest mnożony przez stosunek D RPL /A RPL . Wykorzystując odpowiednie funkcje przenoszenia, D RPL i A RPL są obliczane z góry przez:

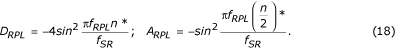
W końcu, skorygowany filtr D* jest przedstawiony jako

i jest pokazany na Rys. 20 jako ślad „c”, gdzie ślady „a” i „b” są odpowiednio filtrem D i filtrem korekcyjnym.

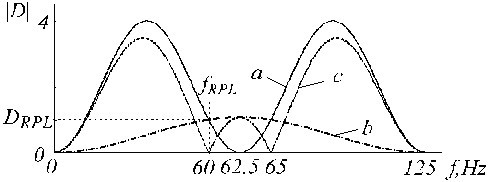
Funkcje przenoszenia a) filtra D, b) pomocniczego filtra korekcyjnego i c) skorygowanego filtra D.

Funkcja przenoszenia filtra K musi zachowywać zero dla f = f RPL , jedność wzmocnienia dla f = 0 oraz liniową odpowiedź fazową. Procedura korekcji filtru K jest podobna do poprzedniej. Filtr pomocniczy jest dany wzorem stosowanym do obliczania poprawek:

A i = X i – Y i , (20)

Wzmocnienie filtra jest równe 1 – K RPL dla f = f RPL , gdzie K RPL jest wzmocnieniem filtra K dla tej samej częstotliwości f RPL . Filtr pomocniczy jest mnożony przez K RPL /(1 – K RPL ) i odejmowany od filtra K. Równanie dla skorygowanego filtra K* jest następujące:

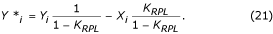
Stała K RPL może być oszacowana przez:

odpowiednio dla krotności nieparzystej lub parzystej.

Przykład korekcji filtra K jest pokazany na Rys. 21, gdzie ślady „a”, „b” i „c” reprezentują pierwotny filtr K, filtr pomocniczy i skorygowany filtr K*.

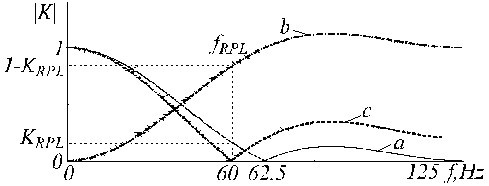
Funkcja przejścia a) filtra K, b) pomocniczego filtra korekcyjnego i c) skorygowanego filtra K.

W przypadku nie-wielokrotnego próbkowania, pojawia się różnica faz pomiędzy trwającymi próbkami EKG a składowymi zakłócającymi B i (równanie 16) umieszczonymi zwykle w tymczasowym buforze FIFO (first-in-first-out). Dlatego też B i musi być modyfikowana i odejmowana od próbek EKG podczas odcinków nieliniowych. Procedura kompensacji jest stosunkowo skomplikowana. Na rys. 22 przedstawiono zawartość bufora tymczasowego. Bieżąca próbka zakłócająca, B i-n *, nie pokrywa się z próbką przywróconą, B i . Jej amplituda musi być przeliczona w celu skompensowania różnicy faz między nimi. Dokonuje się tego za pomocą nowego filtru o liniowej odpowiedzi fazowej i wzmocnieniu równym jedności dla f = f RPL , oznaczanego jako filtr B. Jest on syntetyzowany na podstawie znanego filtru K, z oknem równym okresowi interferencji. W przypadku nieparzystego n*, można go opisać jako:

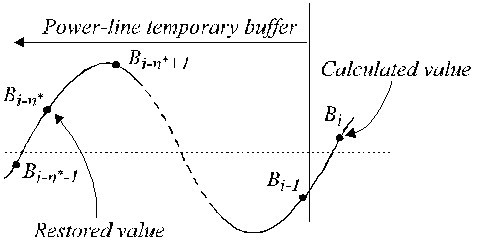
Przywrócone wartości w buforze tymczasowym.

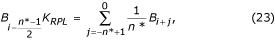
gdzie K RPL jest wzmocnieniem dla zakłóceń filtru uśredniającego danego równaniem (22).

Przywrócona wartość bufora B i może być obliczona przez:

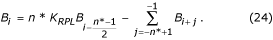
W przypadku parzystego n*:

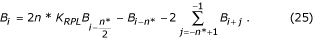
Funkcja przenoszenia filtra B jest pokazana na Rys. 23.

Funkcje przenoszenia a) filtra B i b) znanego filtra K.

Uogólniona struktura przedstawiona jest na rys. 24, gdzie moduły procedury odejmowania są następujące:

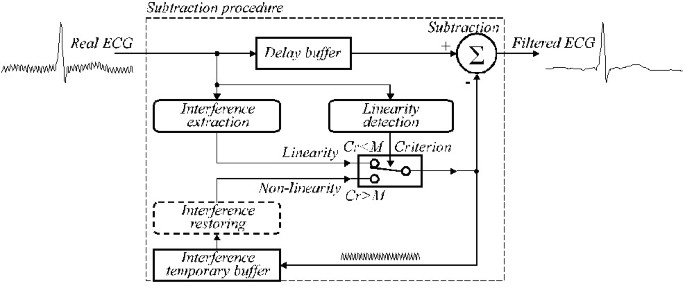
Uogólniona struktura procedury odejmowania.

• Detekcja liniowości. Filtr D jest stosowany do oceny liniowości sąsiedztwa każdej próbki sygnału.

• Wyodrębnianie zakłóceń. (1-K)-filtr jest stosowany do obliczenia składowej interferencyjnej.

• Kryterium. Warunek Cr <M wysyła wyekstrahowaną lub przywróconą interferencję PL do Subtraction.

• Bufor tymczasowy interferencji. Wyekstrahowana lub odtworzona składowa zakłócenia używana jako korekcja w segmencie nieliniowym jest zapisywana na pozycji zablokowanej z trwającą fazą zakłócenia linii energetycznej.

• Przywracanie zakłóceń. Filtr B jest wywoływany w przypadku nie-wielokrotnego próbkowania w celu przywrócenia prawdziwych wartości korekcyjnych, które muszą być odjęte od próbek sygnału wejściowego w segmentach nieliniowych.

• Bufor opóźnienia. Kompensuje opóźnienie, które pojawia się wraz z filtrem D i (1-K)-filtrem i jest niezbędne, jeśli procedura jest wykonywana w czasie quasi-rzeczywistym. W przeciwnym razie, bufor może być pominięty.

• Subtraction. Wyekstrahowana lub przywrócona wartość zakłóceń jest odejmowana od opóźnionego sygnału wejściowego, aby otrzymać „czysty” sygnał EKG. W przypadku nieliniowości zarówno ekstrakcja zakłóceń jak i odejmowanie realizują filtr K.

Ulepszony algorytm według uogólnionej struktury został przetestowany off-line. Wyniki dla f S = 250 Hz i f RPL = 60 Hz pokazano na rys. 25.

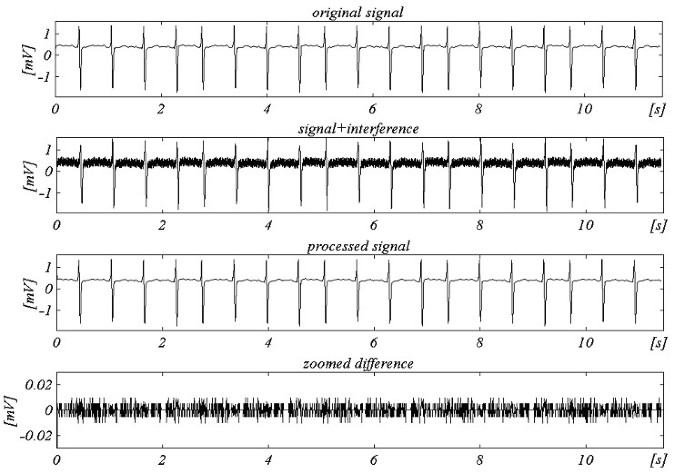
Przykład dla niepróbkowania wielokrotnego z fRPL = 60 Hz i fS = 250 Hz.

.