Abstract
Światło podróżuje przez próżnię z prędkością c bez względu na ruch źródła światła lub ramki odniesienia obserwatora. W konsekwencji, światło potrzebuje pewnego czasu na przebycie drogi od źródła światła do obserwatora w przestrzeni, tak że emisja światła i obserwacja wyemitowanego światła nie są równoczesne. Na podstawie tych rozważań zaproponowano metodę pomiaru prędkości absolutnej obserwatora, która może być wykorzystana do określania stanu ruchu statku kosmicznego z wnętrza zamkniętej kabiny. W pracy tej wprowadzono również nowe wyjaśnienie transformacji Lorentza.
Słowa kluczowe
układ współrzędnych, układ odniesienia, ruch, prędkość absolutna, względność, transformacja Lorentza, czas, przestrzeń, obserwator, źródło światła
Poniższa analiza przedstawia praktyczne podejście do pomiaru prędkości absolutnej obserwatora, które mogłoby być wykorzystane do wyznaczania stanu ruchu statku kosmicznego z wnętrza zamkniętej kabiny. Pojęcie prędkości absolutnej ogólnie odnosi się do standardowej jednolitej prędkości różnych obiektów układu fizycznego względem postulowanej nieruchomej przestrzeni, która istnieje niezależnie od obiektów fizycznych w niej zawartych (tj. przestrzeni absolutnej). W niniejszym artykule przedstawiamy podejście oparte na kinematyce sztywnej pokazujące, że prędkość absolutna obserwatora może być wyznaczona na podstawie faktu, że światło podróżuje przez próżnię z prędkością c niezależnie od ruchu źródła światła i ramki odniesienia obserwatora. W związku z tym światło potrzebuje pewnego czasu na przebycie drogi od źródła światła do obserwatora w przestrzeni, tak że emisja światła i obserwacja wyemitowanego światła nie są równoczesne.
W proponowanej analizie podajemy najpierw następujące konwencje dla rozważanych układów współrzędnych. Zakładamy kartezjański układ współrzędnych składający się z trzech parami prostopadłych osi wychodzących z punktu (0,0,0), gdzie każdy punkt P w przestrzeni może być określony przez jego współrzędne wzdłuż osi x, y, i z, reprezentowane przez uporządkowaną parę liczb rzeczywistych (x,y,z). Przyjmuje się, że inercyjny układ odniesienia S jest reprezentowany przez przestrzenny prostokątny układ współrzędnych (x,y,z), którego początek znajduje się w O. Seria standardowych zegarów (zwanych zegarami S) jest umieszczona w stacjonarnych punktach S. Zegary S są wzajemnie kalibrowane (tj. zapewniają równoważne odczyty w tej samej chwili w czasie) na podstawie transmisji i odbioru sygnału świetlnego. W szczególności, w czasie tA, wiązka światła jest rzutowana z zegara A na zegar B, który jest następnie odbity w czasie tB przez zegar B z powrotem w kierunku zegara A, i dociera do zegara A w czasie tA’. Jeśli 
, oba zegary są skalibrowane. Dla dowolnego zdarzenia znajdującego się na współrzędnych x,y,z, jego współrzędna czasowa t jest określona przez odczyt zegara S związanego ze zdarzeniem. Podobnie ustanawia się inny inercyjny układ odniesienia S’ oparty na drugim przestrzennym prostokątnym układzie współrzędnych (x’,y’,z’), którego początkiem jest O’, a w punktach stacjonarnych układu odniesienia S’ umieszcza się kolejną serię wzajemnie skalibrowanych zegarów wzorcowych (zegary S’). Dla każdego zdarzenia zlokalizowanego na współrzędnych x’,y’,z’, jego współrzędna czasowa t’ jest określona przez odczyt zegara S’ związanego ze zdarzeniem.
Ponieważ odpowiednie początki współrzędnych przestrzennych i czasowych, jak również kierunki osi współrzędnych mogą być w dużym stopniu wybierane arbitralnie, związki pomiędzy S i S’ stosowane w niniejszym dokumencie są oparte na następujących konwencjach, które zostały zastosowane dla uproszczenia.
(1) W określonej chwili w czasie, początki i osie współrzędnych obu układów są nałożone na siebie, a zegary odpowiednio umieszczone w O i O’ są ustawione na zero, tj, 
.
(2) Osie x i x’ są zbieżne w kierunku względnego ruchu S i S’; zatem x i x’ są zbieżne przez cały czas, natomiast y i y’ oraz z i z’ są równoległe.
(3) S’ porusza się wzdłuż kierunku +x układu S.
Proponowana analiza opiera się na podstawowej zasadzie, że światło w próżni porusza się ze stałą prędkością c niezależnie od ruchu obserwatora lub źródła światła. W związku z tym, definiujemy tutaj prędkość bezwzględną U obserwatora, która z założenia jest liniowa i jednostajna, jako 
, gdzie f(φ) reprezentuje funkcję geometrycznej relacji pomiędzy kierunkiem sygnału świetlnego a kierunkiem U, oznaczoną tutaj jako φ.
W proponowanej analizie przedstawione są dwa nowe wyjaśnienia względności czasu i długości, które różnią się od wyjaśnień Einsteina (proszę odnieść się do „O elektrodynamice poruszających się ciał”). Wyjaśnienia te są wprowadzone w następujących rozdziałach.
Względność czasu
W związku ze skończoną prędkością światła, pewien czas jest wymagany, aby światło przebyło drogę od źródła światła do obserwatora w przestrzeni. Można zatem wywnioskować, że emisja światła i jego obserwacja nie mogą być jednoczesne. Na podstawie stałości prędkości światła i warunków przedstawionych na rysunku 1, określamy następujące czynniki. Położenia źródła światła i obserwatora w chwili 
, w której źródło światła emituje światło (oznaczane jako zdarzenie R), są dane odpowiednio jako A i H0. W czasie rozchodzenia się światła od 
do 
obserwator przebywa odległość U∙T od położenia H0 do H, gdzie odbiera wyemitowane światło. Odpowiednio, definiujemy 
jako odległość l pomiędzy położeniem obserwatora przy odbiorze sygnału świetlnego w 
a położeniem źródła światła przy emisji światła w 
. Dzięki stałości prędkości światła, 
. Odległość 
jest równa U∙T. Wreszcie definiujemy 
jako odległość l0 między położeniem obserwatora w punkcie 
a położeniem źródła światła w punkcie 
. W tym miejscu wprowadzamy rozważania na temat położenia obserwatora w punkcie 
, o którym wcześniej sądzono, że nie ma fizycznego znaczenia. Jeśli stany ruchu obserwatora i źródła światła są równoważne, dane jest l0, tak że U może być obliczone poprzez trójkątne relacje zilustrowane na rysunku 1.
W obecnej pracy, czas zdarzenia jest mierzony przy użyciu następującej metody. Zarówno obserwator jak i zegar są umieszczone w punkcie początkowym. Kiedy sygnał świetlny reprezentujący wystąpienie zdarzenia dotrze do obserwatora, czas dotarcia światła będzie odpowiadał czasowi wskazywanemu przez zegar. Zaletą tej korespondencji jest to, że jest ona zawsze związana z położeniem obserwatora, który posługuje się zegarem. Jak widać na rysunku 1, punkt przestrzenny O3 można zdefiniować w oparciu o położenie źródła światła podczas emitowania światła w punkcie 
, a punkt przestrzenny O2 można zdefiniować w oparciu o położenie obserwatora podczas odbierania światła w punkcie 
. Jednakże sposób definiowania punktu przestrzennego O1, w którym znajduje się obserwator, gdy źródło światła emituje światło o natężeniu 
, nie jest oczywisty. Aby rozwiązać ten problem, wprowadzamy pojęcia spoczynku absolutnego (tj. 
) i ruchu absolutnego (tj. 
). Zastępujemy pojedynczego poruszającego się obserwatora w H0 i H dwoma obserwatorami H1 i H2 znajdującymi się w spoczynku odpowiednio w punktach przestrzennych O1 i O2, podczas gdy źródło światła A znajduje się w spoczynku w punkcie przestrzennym O3. Każdy z obserwatorów i źródło światła mają skalibrowane zegary standardowe, a A emituje sygnał świetlny o godzinie 
, oznaczany jako zdarzenie R0. Kiedy obserwator H1 odbiera sygnał świetlny poruszający się z prędkością c, odczyt zegara wynosi T0, a kiedy odbiera go H2, odczyt wynosi T. W związku z tym odległości 
i 
można zdefiniować na podstawie odpowiednich czasów podróży sygnału świetlnego w następujący sposób:
, (1)
i
. (2)
Zgodnie z zależnościami trójkątnymi pokazanymi na rysunku 1, transformacja zdarzenia R0 pomiędzy obserwatorami H1 i H2 jest dana w następujący sposób.
(3) 
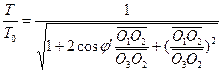(4)
Tutaj 
jest kątem pomiędzy prostą O3O1 a osią x, a 
jest kątem pomiędzy prostą O3O2 a osią x.
Powracając teraz do warunków pojedynczego poruszającego się obserwatora, zakładamy, że w układzie S zarówno obserwator H, jak i źródło światła A posługują się skalibrowanym zegarem wzorcowym. W chwili zdarzenia R, źródło światła A znajduje się w punkcie przestrzennym O3, a obserwator H w punkcie O1. Chwila, w której sygnał świetlny dociera do punktu przestrzennego O1 odpowiada wskazaniu zegara S równemu T0. Kiedy obserwator H odbiera sygnał świetlny, odczyt wynosi T, a H znajduje się w punkcie O2.
Oczywiście H nie może zaobserwować zdarzenia R w punkcie O1. Aby rozwiązać ten problem, inny obserwator H- jest umieszczony w układzie S w punkcie O1 odpowiadającym 
, gdzie pozycja H- jest wykorzystana do zdefiniowania przestrzennego punktu O1. Następnie, transformację zdarzenia R pomiędzy obserwatorami H- i H można uzyskać za pomocą równania (3) w następujący sposób. 
(5)
Więc, równania (3) i (4) można przepisać w następujący sposób.
(6) 
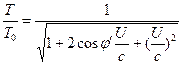(7)
e Zauważmy również, że dla 
, równania (6) i (7) upraszczają się do następującego.
(8) 
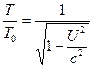(9)
W związku z tym, na podstawie powyższej analizy, z równania (6) można otrzymać prostą metodę wyznaczania U, przy założeniu, że 
(φ) jest znane.
Dla uproszczenia, jako ramę odniesienia wybiera się źródło światła o równoważnym stanie ruchu jak obserwatorzy. Obserwator ustawiony jest w środku prostego sztywnego pręta poruszającego się ruchem jednostajnym liniowym, a sygnały świetlne z różnych miejsc na pręcie docierają do obserwatora w różnym czasie. Obserwator wykrywa ugięcie pręta w jego położeniu o kąt ugięcia 
, który można otrzymać z równania (8).
Dzięki tej metodzie można wyznaczyć stan ruchu statku kosmicznego z zamkniętej kabiny.
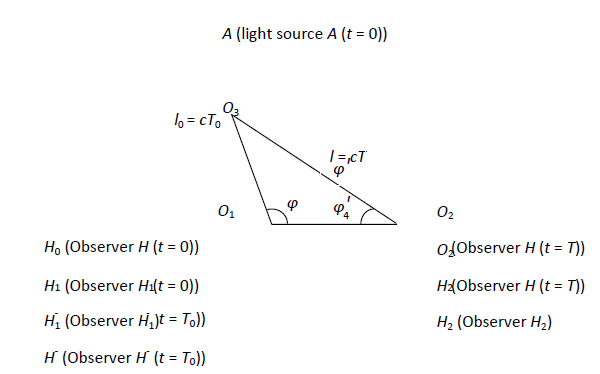
Rysunek 1: stany ruchu obserwatora i źródła światła
Względność długości
W powyższej analizie wprowadzono dwie długości, tj. 
i 
. W tym przypadku rozważamy długość pręta, o którym zakłada się, że jest nieruchomym sztywnym prętem o długości L w swoim układzie współrzędnych, dla którego L mierzy się za pomocą nieruchomego przymiaru łaty, i gdzie oś pręta pokrywa się z osią x układu współrzędnych poruszającego się ruchem jednostajnym liniowym wzdłuż kierunku +x z prędkością bezwzględną U. Zakłada się, że L jest wyznaczona przez dwie operacje zdefiniowane poniżej.
(a) Obserwator znajduje się w tym samym ruchomym układzie współrzędnych co pręt i łata pomiarowa, a L mierzy się przez nałożenie na siebie pręta i łaty pomiarowej.
(b) Za pomocą kilku zegarów umieszczonych we współrzędnych stacjonarnych, które poruszają się synchronicznie, obserwator mierzy położenie dwóch końców pręta we współrzędnych stacjonarnych w określonej chwili t, a odległość między tymi dwoma położeniami mierzy się za pomocą stacjonarnego łaty pomiarowej. 
jest długością obliczoną w wyniku operacji (a), która jest tu oznaczana jako długość pręta we współrzędnych ruchomych. 
jest długością obliczoną z operacji (b), która jest tu oznaczana jako długość ruchomego pręta we współrzędnej stacjonarnej. Jest oczywiste, że 
i 
są różne.
Zakładamy, że w układzie S obserwator H- znajduje się w tym samym stanie ruchu co H. Wówczas, jak pokazano na rysunku 1, H- znajduje się w punkcie O1 podczas odbierania sygnału świetlnego w punkcie 
, a jednocześnie obserwator H znajduje się w punkcie O4. Zatem, t=0,04
jest odległością między H- a H w chwili 
, a 
. (10)
jest odległością przebytą przez obserwatora H w przedziale czasu od T0 do T, taką, że
. (11)
jest odległością między H- w chwili 
a H w chwili 
, taką, że
. (12)
Jako takie, można wydedukować następujące wyrażenie.
(13)
Następnie rozważymy transformacje współrzędnych i czasu pomiędzy dwoma ruchomymi układami współrzędnych, z których oba poruszają się z jednostajną prędkością liniową, co stanowi nowe wyjaśnienie transformacji Lorentza.
Zakładając, że obserwator H (w układzie S), obserwator H’ (w układzie S’) i źródło światła A” (w układzie S”) posługują się indywidualnie skalibrowanymi zegarami wzorcowymi, w chwili 
źródło światła A” emituje sygnał świetlny, oznaczony jako zdarzenie R”. W chwili zdarzenia R”, A” znajduje się w punkcie O3, a obserwatorzy H i H’ są zbieżni. Kiedy obserwator H odbiera sygnał świetlny, wskazanie zegara S wynosi T, a H znajduje się w punkcie O1. Gdy obserwator H’ odbiera sygnał świetlny, wskazanie zegara S’ wynosi T’, a H’ znajduje się w punkcie O2. Wówczas transformację zdarzenia R” pomiędzy obserwatorami H’ i H można obliczyć z równania (3), gdzie
. (14)
Tutaj u jest prędkością względną między obserwatorami H’ i H, co daje następujące transformacje. 
(15) 
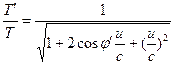(16)
Z 
można wyprowadzić następujące zależności: 
. (17)
W przypadku 
i 
, równanie (16) upraszcza się do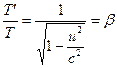
. (18)
Więc można wydedukować następujące relacje przekształceń:
, (19)
, (20)
, (21)
. (22)
Ponadto, gdy 
, 
, (23)
i 
, (24)
, (25)
, (26)
. (27)