1D & 3D Convoluções explicadas com… MS Excel!

Começamos com Convoluções 2D no primeiro post porque as convoluções ganharam popularidade significativa após os sucessos no campo da Visão Computacional. Como as tarefas neste domínio usam imagens como inputs, e as imagens naturais geralmente têm padrões ao longo de duas dimensões espaciais (de altura e largura), é mais comum ver exemplos de Convoluções 2D do que Convoluções 1D e 3D.

Mais recentemente, porém, houve um grande número de sucessos na aplicação de convoluções em tarefas de processamento de linguagem natural também. Como as tarefas neste domínio usam texto como inputs, e o texto tem padrões ao longo de uma única dimensão espacial (ou seja, tempo), as Convoluções 1D são um ótimo ajuste! Podemos usá-las como alternativas mais eficientes às tradicionais redes neurais recorrentes (RNNs), tais como LSTMs e GRUs. Ao contrário das RNNs, elas podem ser executadas em paralelo para cálculos realmente rápidos.

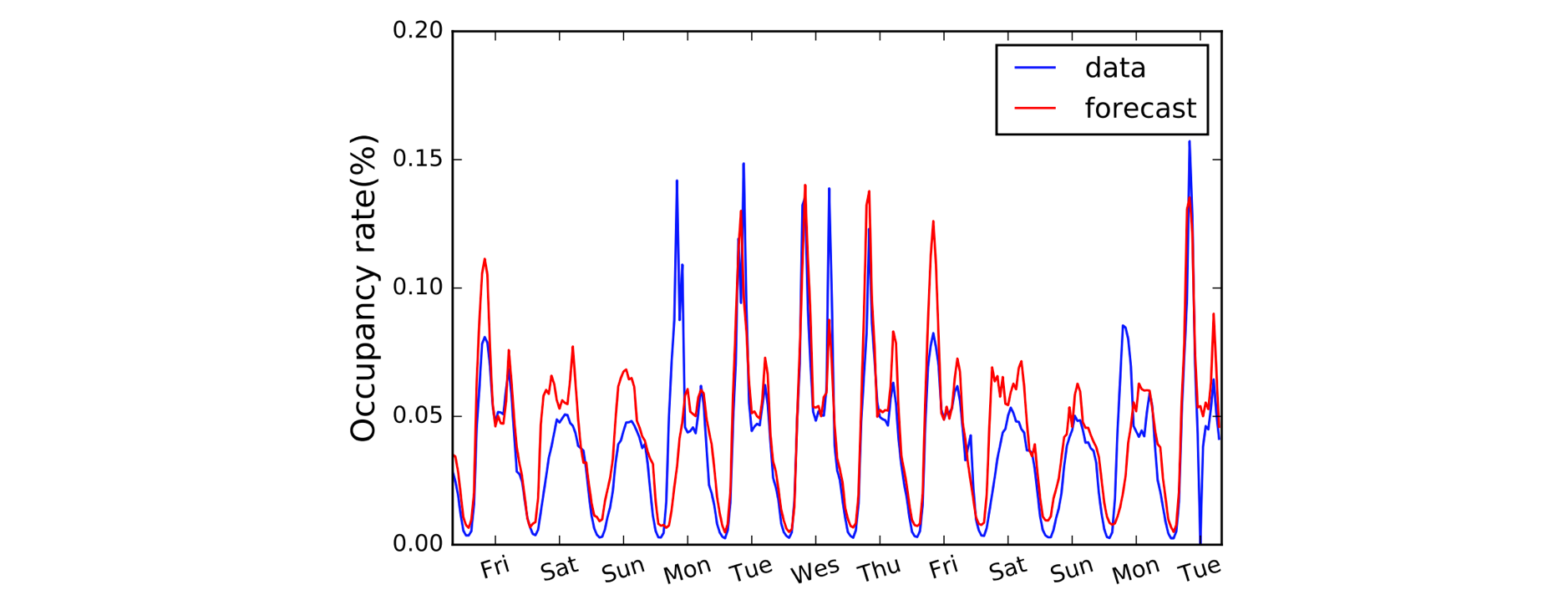
Outro domínio que se beneficia das Convoluções 1D é a modelagem de séries temporais. Como antes, temos uma única dimensão espacial nos nossos dados de entrada (isto é, tempo), e queremos captar padrões ao longo de períodos de tempo. Frequentemente chamamos este tipo de dados de ‘sequencial’ porque pode ser visto como uma sequência de valores. E a dimensão espacial que muitas vezes chamamos de dimensão ‘temporal’. O uso de Convoluções 1D antes de RNNs também é bastante comum: o modelo LSTNet é um exemplo disso e suas previsões para a previsão de tráfego são mostradas abaixo.

A, B, C. É fácil como (1,3,3) ponto (2,0,1) = 5.

Com as convenções de nomenclatura esclarecidas, vamos agora dar uma olhada mais de perto na aritmética. Estamos com sorte porque as Convoluções 1D são na verdade apenas uma versão simplificada da Convolução 2D!

Trabalhando através do cálculo de um único valor de saída, podemos aplicar o nosso kernel de tamanho 3 à região de tamanho equivalente no lado esquerdo da nossa matriz de entrada. Nós calculamos o ‘produto ponto’ da região de entrada e do kernel, que para recapitular é apenas o produto em forma de elemento (ou seja, multiplicar os pares de cores) seguido por uma soma global para obter um único valor. Então neste caso:

(1*2) + (3*0) + (3*1) = 5

Aplicamos a mesma operação (com o mesmo kernel) às outras regiões do array de entrada para obter o array de saída completo de (5,6,7,2); ou seja, deslizamos o kernel por todo o array de entrada. Ao contrário de Convoluções 2D, onde deslizamos o kernel em duas direções, para Convoluções 1D apenas deslizamos o kernel em uma única direção; esquerda/direita neste diagrama.

Avançado: uma Convolução 1D não é o mesmo que uma Convolução 1×1 2D.

Codificando coisas para cima

Insurpreendentemente, precisaremos de um Conv1D Bloco em Gluon para a nossa Convolução 1D. Definimos a forma do kernel como 3, e como estamos apenas trabalhando com um único kernel neste exemplo, vamos especificar channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Agora podemos passar nossa entrada para o bloco conv usando um kernel predefinido.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

O que muda com o padding, stride e dilatação?

Vimos o efeito do padding, stride e dilatação no último post em Convoluções 2D, e é muito semelhante para Convoluções 1D. Com o acolchoamento, desta vez só acolchoamos ao longo de uma única dimensão (a dimensão temporal). O nosso diagrama representa o tempo através do eixo horizontal, por isso, almofadamos à esquerda e à direita dos dados de entrada (e não acima e abaixo como no exemplo da Convolução 2D). Com stride e dilatação, nós só os aplicamos ao longo da dimensão temporal também. Assim um exemplo com padding e stride ficaria da seguinte forma:

Adicionamos dois argumentos adicionais no código: padding=1 e strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Avançado: as dimensões dos dados de entrada devem estar em conformidade com uma ordem particular chamada layout. Por padrão, a convolução 1D espera ser aplicada aos dados de entrada do formato ‘NCW’, ou seja, tamanho do lote (N) * canais (C) * largura/tempo (W). E para Convoluções 2D o padrão é NCHW, ou seja, tamanho do lote (N) * canais (C) * altura (H) * largura (W). Veja o argumento layout de Conv1D e Conv2D.

.