3D Reconstrução

Nesta prática, a intenção é programar a lógica necessária para permitir ao robô kobuki gerar uma reconstrução 3D da cena que está a receber através das suas câmaras esquerda e direita.

Instalação

Instalar a Infra-estrutura Geral da Academia de Robótica JdeRobot.

>

Como executar a sua solução?

Navigar para o diretório 3d_reconstruction

cd exercises/3d_reconstruction

Launch Gazebo com o mundo kobuki_3d_reconstruction através do comando

roslaunch ./launch/3d_reconstruction_ros.launch

Então você tem que executar a aplicação acadêmica, que irá incorporar o seu código:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Como realizar o exercício?

Para realizar o exercício, você tem que editar o arquivo MyAlgorithm.py e inserir nele seu código, que reconstrói pontos 3d a partir das duas vistas estéreo.

Onde inserir o código?

No ficheiro MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Interface de programação de aplicações

• self.getImage('left') – para obter a imagem esquerda
• self.getImage('right') – para obter a imagem direita
• self.point.PlotPoint(position, color) – para traçar o ponto na ferramenta 3d

Navegar na Interface GUI

Baseado no rato: Segurar e arrastar para se mover pelo ambiente. Rolar para aumentar ou diminuir o zoom

Baseado no teclado: Teclas de setas para se mover pelo ambiente. Teclas W e S para aumentar ou diminuir o zoom

Teoria

Na visão e computação gráfica, a reconstrução 3D é o processo de determinar o perfil 3D de um objeto, assim como conhecer a coordenada 3D de qualquer ponto do perfil. A reconstrução pode ser feita da seguinte forma:

• Baseado em Hardware: A abordagem baseada em hardware requer que utilizemos o hardware específico para a tarefa de reconstrução. O uso de luz estruturada, localizador de alcance de laser, medidor de profundidade e métodos radiométricos são alguns exemplos.

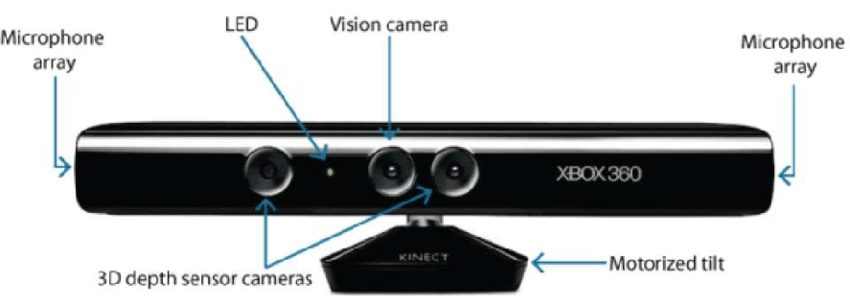
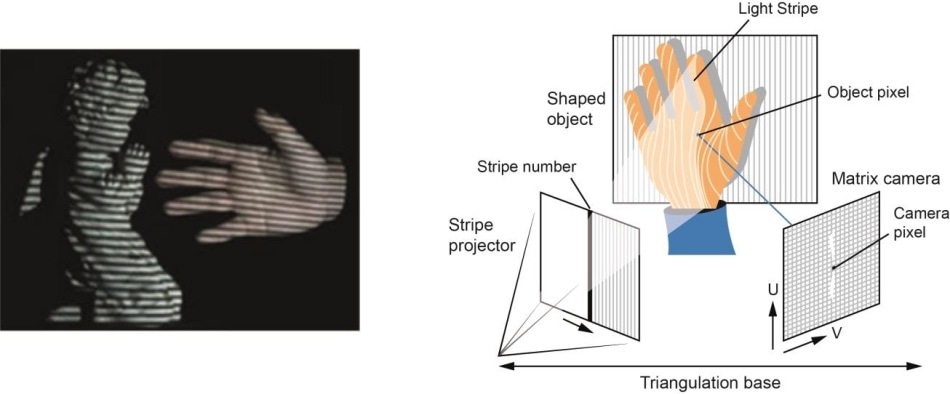
• Baseado em software: A abordagem baseada em software baseia-se nas capacidades de computação do computador para determinar as propriedades 3D do objecto. Forma a partir de sombras, textura, visão estéreo e homografia são alguns bons métodos.

Neste exercício nosso objetivo principal é realizar a reconstrução 3d usando uma abordagem baseada em software, particularmente a reconstrução 3d em visão estéreo.

Geometria Epipolar

Quando duas câmeras vêem uma cena 3D a partir de duas posições diferentes, há uma série de relações geométricas entre os pontos 3D e suas projeções sobre as imagens 2D que levam a restrições entre os pontos de imagem. O estudo destas propriedades e restrições é chamado de Geometrias Epipolares. A imagem e explicação abaixo pode generalizar a idéia:

Suponha um ponto X no espaço 3d é imitado em duas vistas, em x na primeira e x' na segunda. Projetando os raios para seus centros de câmera através dos planos da imagem, obtemos uma superfície plana, denotada por π.

Supondo agora que sabemos apenas x, podemos perguntar como o ponto correspondente x' é restringido. O plano π é determinado pela linha de base (linha que liga os centros da câmera) e pelo raio definido por x. De cima, sabemos que o raio correspondente ao ponto desconhecido x' se encontra em π, daí que o ponto x' se encontra na linha de intersecção l' de π com o segundo plano de imagem. Esta linha é chamada de linha epipolar correspondente a x. Esta relação nos ajuda a reduzir o espaço de busca do ponto na imagem da direita, de um plano para uma linha. Algumas definições importantes a notar são:

• A epipolo é o ponto de intersecção da linha que une os centros da câmara (a linha de base) com o plano da imagem.

• Um plano epipolar é um plano que contém a linha de base.

• Uma linha epipolar é a intersecção do plano epipolar com o plano da imagem.

Reconstrução de Stereo

Reconstrução de Stereo é um caso especial da reconstrução 3d acima, onde os dois planos da imagem são paralelos entre si e igualmente distantes do ponto 3d que queremos traçar.

Neste caso a linha epipolar para ambos os planos da imagem é a mesma, e são paralelas à largura dos planos, simplificando melhor a nossa restrição.

3D Algoritmo de Reconstrução

O algoritmo de reconstrução consiste em 3 passos:

1. Detectar os pontos de característica num plano de imagem
2. Detectar o ponto de característica correspondente ao encontrado acima
3. Triangular o ponto no espaço 3d

Vejamo-los um a um

Detecção do ponto de característica

Detecção do ponto de característica é uma vasta área de estudo onde vários algoritmos já estão estudados. Os algoritmos Harris Corner Detection e Shi-Tomasi usam valores próprios para obter um bom ponto de característica. Mas, o problema é que precisamos de muitos pontos para a Reconstrução 3D, e estes algoritmos não serão capazes de nos fornecer um número tão grande de pontos de característica.

Por isso, usamos pontos de borda como nossos pontos de característica. Pode haver ambiguidade na sua detecção na próxima etapa do algoritmo. Mas, o nosso problema é resolvido tomando as bordas como pontos de característica. Um detector de bordas realmente legal é o Algoritmo de Detecção de Bordas Canny. O algoritmo é bastante simples e confiável em termos de geração de bordas.

Extração de pontos de característica

O uso da restrição epipolar realmente simplifica a complexidade de tempo do nosso algoritmo. Para problemas gerais de reconstrução 3d, temos de gerar uma linha epipolar para cada ponto de um quadro de imagem, e depois procurar nesse espaço de amostra o ponto correspondente no outro quadro de imagem. A geração da linha epipolar também é muito fácil no nosso caso, é apenas a iterpolação da linha paralela da imagem esquerda para o plano da imagem direita.

A verificação da correspondência entre as imagens envolve muitos algoritmos, como a soma das diferenças quadriculadas ou a minimização de energia. Sem ir muito fundo, usando um simples filtro de Correlação também é suficiente o nosso caso de uso.

Triangulação

Triangulação em termos simples é apenas calcular onde o ponto 3d vai ficar usando os dois pontos determinados nos planos da imagem.

Na realidade, a posição dos pontos da imagem não pode ser medida exactamente. Para câmeras em geral, pode haver distorções geométricas ou físicas. Portanto, muita matemática vai para trás minimizando esse erro e calculando a projeção de pontos 3d mais precisa. Consulte este link para um modelo simples.

Dicas

Sugestões simples fornecidas para ajudá-lo a resolver o exercício 3d_reconstruction. A biblioteca OpenCV é usada extensivamente para este exercício.

Configuração

Usando a API do exercício, podemos facilmente recuperar as imagens. Além disso, depois de obter as imagens, é uma boa idéia realizar uma filtragem bilateral nas imagens, pois há alguns detalhes extras que não precisam ser incluídos durante a reconstrução 3d. Confira as ilustrações para os efeitos de realizar a filtragem bilateral.

Calculando Correspondências

OpenCV já possui filtros de correlação embutidos que podem ser chamados através de matchTemplate(). Cuidar de casos extremos como bordas e cantos.

Uma boa observação é que os pontos da esquerda terão correspondência na parte esquerda e os pontos da direita terão correspondência na parte direita. Usando esta observação, podemos facilmente acelerar o cálculo da correspondência.

Plotar os pontos

A função manual ou baseada no OpenCV triangulatePoints funciona bem para triangulação. Basta cuidar de todas as formas e tamanhos de matrizes enquanto executa as implementações algébricas.

Cuidado com a diferença entre coordenadas 3D simples e coordenadas 4D homogêneas. Confira este vídeo para detalhes. A simples divisão do vector 4d completo pela sua 4ª coordenada dá-nos as coordenadas 3d.

Devido a implementações variadas de utilizadores, o utilizador pode ter de ajustar a escala e o offset dos pontos triangulados de modo a torná-los visíveis e representáveis na interface GUI. Reduzir o vetor de coordenadas 3D por um valor entre 500 a 1000 funciona bem. Também um offset de 0 a 8 funciona bem.

Illustrações