Grupo Abeliano | CDhistory

Um grupo Abeliano é um grupo para o qual os elementos se deslocam (ou seja, para todos os elementos e ). Grupos abelianos, portanto, correspondem a grupos com tabelas de multiplicação simétricas.

Todos os grupos cíclicos são abelianos, mas um grupo abeliano não é necessariamente cíclico. Todos os subgrupos de um grupo Abeliano são normais. Em um grupo Abeliano, cada elemento está em uma classe conjugada por si só, e a tabela de caracteres envolve poderes de um único elemento conhecido como gerador de grupo.

Na linguagem Wolfram, a função AbelianGroup representa o produto direto dos grupos cíclicos de graus , , ….

Nenhuma fórmula geral é conhecida por dar o número de grupos finitos não isomórficos de uma dada ordem de grupo. Entretanto, o número de grupos finitos abelianos não-isomórficos de qualquer ordem de grupo dado é dado por escrito como

(1)

onde os são factores primordiais distintos, então

(2)

where é a função de partição, que é implementada na linguagem Wolfram como FiniteAbelianGroupCount. Os valores de para , 2, … são 1, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, … (OEIS A000688).

As ordens menores para as quais , 2, 3, … existem grupos abelianos não isomórficos são 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), onde 0 denota um número impossível (ou seja, não um produto de números de partição) de grupos de Abelianos não isomórficos. Os valores “em falta” são 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Os números incrementais dos grupos abelianos em função da ordem são 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), que ocorrem para as ordens 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

O teorema da decomposição Kronecker afirma que todo grupo finito abeliano pode ser escrito como um produto direto de grupos cíclicos de ordem de grupo de potência primária. Se a ordem de grupo de um grupo finito é um prime , então existe um único grupo Abeliano de ordem (denoted ) e nenhum grupo não-Abeliano. Se a ordem do grupo é um grupo prime ao quadrado , então existem dois grupos Abelianos (denotado e . Se a ordem do grupo é um cubo primo , então há três grupos abelianos (indicado , , e ), e cinco grupos no total. Se a ordem é um produto de dois primes e , então existe exatamente um grupo Abeliano de ordem de grupo (denoted ).

Outro resultado interessante é que se denota o número de grupos abelianos não isomórficos de ordem de grupo , então

(3)

where é a função zeta de Riemann.

Os números dos grupos de ordens abelianas são dados por 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) por , 2, …. Srinivasan (1973) também mostrou que

(4)

where

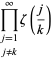			(5)
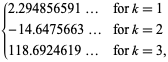			(6)

(OEIS A021002, A084892, e A084893) e é novamente a função zeta de Riemann. Note que Richert (1952) deu incorrectamente . As somas também podem ser escritas nas formas explícitas