Intervalos de Tolerância
Esta secção contém detalhes estatísticos para intervalos de tolerância unidireccionais e bidireccionais.
Intervalos de distribuição normal
Intervalo unilateral
O intervalo unilateral é calculado da seguinte forma:
Limite inferior = 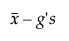
Limite superior = 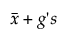
where
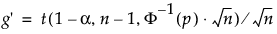
s é o desvio padrão
t é o quantil a partir do nãodistribuição t central
Φ-1 é o quantil normal padrão
Intervalo bilateral
O intervalo bilateral é calculado da seguinte forma:
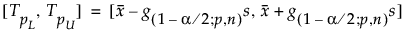
onde s é o desvio padrão e g(1-α/2; p,n) é uma constante.
Para determinar g, considere a fração da população capturada pelo intervalo de tolerância. Tamhane e Dunlop (2000) dão essa fração da seguinte forma:
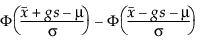
onde Φ denota o cdf normal padrão (função de distribuição cumulativa).
>Por isso, g resolve a seguinte equação:
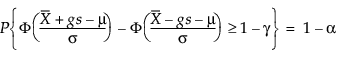
Onde 1 – γ é a fração de todas as observações futuras contidas no intervalo de tolerância.
Para mais informações sobre intervalos de tolerância baseados na distribuição normal, veja as Tabelas J.1a, J.1b, J.6a e J.6b de Meeker et al. (2017).
Intervalos não-paramétricos
Limite inferior unilateral
O limite inferior de tolerância de 100(1 – α)% unilateral para conter pelo menos uma proporção β da distribuição amostrada de uma amostra de tamanho n é a estatística de ordem x(l). O índice l é calculado da seguinte forma:
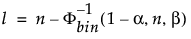
onde Φ-1bin(1-α, n, β) é o (1 – α)o quantil da distribuição binomial com n ensaios e probabilidade de sucesso β.
O nível de confiança real é calculado como Φbin(n-l, n, β), onde Φbin(x, n, β) é a probabilidade de uma variável aleatória binomial distribuída com n tentativas e probabilidade de sucesso β sendo menor ou igual a x.
Nota que para calcular um intervalo de tolerância unilateral inferior sem distribuição, o tamanho da amostra n deve ser pelo menos tão grande quanto 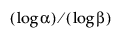 .
.
Limite superior unilateral
O limite superior de tolerância unilateral 100(1 – α)% para conter pelo menos uma proporção β da distribuição amostrada de uma amostra de tamanho n é a estatística de ordem x(u). O índice u é calculado da seguinte forma:
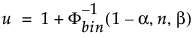
onde Φ-1bin(1-α, n, β) é o (1 – α)o quantil da distribuição binomial com n ensaios e probabilidade de sucesso β.
O nível de confiança real é calculado como Φbin(u-1, n, β), onde Φbin(x, n, β) é a probabilidade de uma variável aleatória binomial distribuída com n ensaios e probabilidade de sucesso β ser menor ou igual a x.
Nota que para calcular um intervalo superior de tolerância sem distribuição unilateral, o tamanho da amostra n deve ser pelo menos tão grande quanto 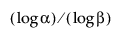 .
.
Intervalo bilateral
O intervalo de tolerância bilateral 100(1 – α)% para conter pelo menos uma proporção β da distribuição da amostra de uma amostra de tamanho n é calculado da seguinte forma:
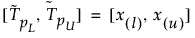
onde x(i) é a estatística da ordem ith e l e u são computados da seguinte forma:
Let ν = n – Φ-1bin(1-α, n, β), onde Φ-1bin(1-α, n, β) é o (1 – α)o quantil da distribuição binomial com n ensaios e probabilidade de sucesso β. Se ν for inferior a 2, não é possível calcular um intervalo de tolerância sem distribuição em dois lados. Se ν for maior ou igual a 2, l = piso(ν/2) e u = piso(n + 1 – ν/2).
O nível de confiança real é calculado como Φbin(u-l-1, n, β), onde Φbin(x, n, β) é a probabilidade de uma variável aleatória binomial distribuída com n tentativas e probabilidade de sucesso β sendo menor ou igual a x.
Nota que para calcular um intervalo de tolerância sem distribuição em dois lados, o tamanho da amostra n deve ser pelo menos tão grande quanto o n na seguinte equação:

Para mais informações sobre intervalos de tolerância sem distribuição, ver Meeker et al. (2017, seg. 5.3).