O procedimento de subtração para eliminação de PL foi elaborado pela primeira vez há cerca de duas décadas. Este procedimento não afeta os componentes do ECG vizinhos à freqüência do PL. Este estudo teórico é realizado para a freqüência básica do PL, mas as conclusões também são válidas para seus harmônicos e, consequentemente, para uma forma de onda de interferência arbitrária. A eficiência do procedimento não depende da amplitude da interferência, desde que o amplificador não esteja saturado. Além disso, o procedimento lida com sucesso com mudanças na amplitude e freqüência da interferência. O procedimento tem sido continuamente melhorado ao longo dos anos, e implementado em milhares de instrumentos de ECG e sistemas assistidos por computador. Abordagens similares também foram publicadas por outros pesquisadores .
- Princípios
- Critério linear
- Compensação das variações de amplitude do PL
- Filtragem linear
- Compensação da variação da frequência PL
- Avaliação da eficiência do procedimento
- Influência do ruído EMG
- Interferência de supressão em ECG de alta resolução
- Caso de dispositivos fornecidos com bateria e sistemas de ECG auxiliados por computador
- A adaptação automática à freqüência nominal do PL
- Desenvolvimento do procedimento teórico
Princípios
O procedimento de subtração é aplicado originalmente com freqüência de amostragem f S , um múltiplo de, e hardware sincronizado com a freqüência PL f PL . O procedimento consiste nos seguintes passos :
-
Segmentos ECG com banda de frequência próxima de zero são continuamente detectados usando um critério apropriado. Eles são referidos como segmentos lineares e são encontrados principalmente nos intervalos PQ e TP, mas também em partes retas suficientemente longas das ondas R e T.
-
As amostras destes segmentos estão em média móvel, ou seja, sujeitos a um filtro de pente de fase linear com o primeiro zero ajustado em f PL . Assim, as amostras filtradas não contêm interferências.
-
As amplitudes de interferência, chamadas correcções, são calculadas para cada uma das amostras bloqueadas de fase, n, no período PL, T PL , subtraindo as amostras filtradas das amostras correspondentes do sinal ECG (original) contaminado.
-
O conjunto de correcções obtidas é continuamente actualizado em segmentos lineares e utilizado em segmentos não lineares (normalmente em torno de complexos QRS e ondas T de alta amplitude) para subtrair a interferência do sinal ECG original.
Um dos primeiros resultados obtidos pelo método de subtracção é mostrado na Fig. 1 . A interferência foi adicionada a um sinal de ECG simulado limpo para avaliar os erros e a eficiência do método.
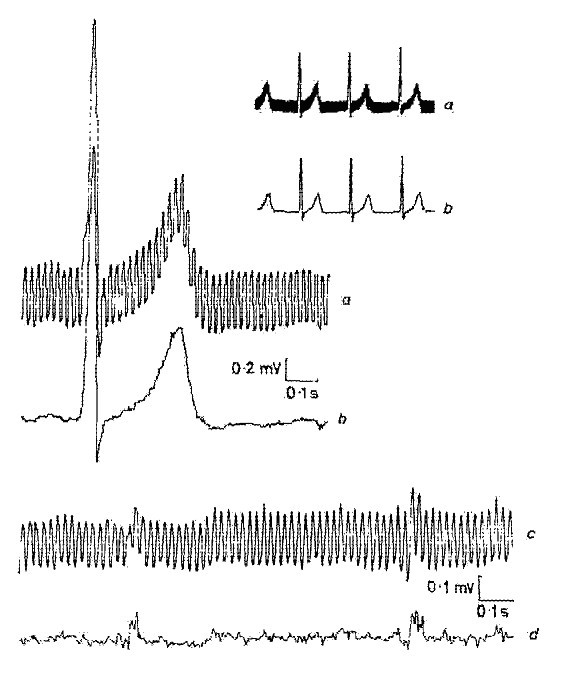
Um dos primeiros resultados obtidos pelo procedimento de subtração.
Critério linear
Critério linear, Cr, geralmente corresponde à segunda diferença do sinal (avaliação matemática da linearidade). O primeiro Cr é definido da seguinte forma. Seis primeiras diferenças consecutivas, FD i , são calculadas usando amostras de sinal, X i , espaçadas em um T PL :
FD i = X i+n – X i , para i = 1 … 6 (1)
A interferência PL nas primeiras diferenças é suprimida se n = f S /f PL . Neste caso n = 5, uma vez que o procedimento foi desenvolvido inicialmente para f PL nominal = 50 Hz e f S = 250 Hz. Além disso, os valores máximos FD max e mínimos FD min são tomados para determinar Cr:
Cr = | FD max – FD min | <M, (2)
onde M é o valor limiar.
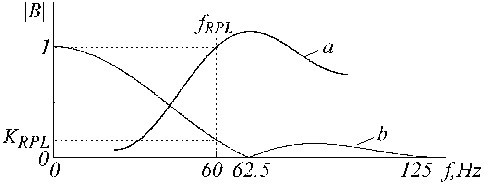
Segmentos lineares e não lineares típicos são mostrados na Fig. 2. O sinal real do ECG (traço a) é sobreposto por interferência (traço b). Os segmentos lineares incluem sinal de baixa frequência e componentes de frequência da linha de potência. Um espectro de frequência aproximado desses segmentos lineares é mostrado na Fig. 3.

Segmentos lineares e não lineares típicos em sinal real de ECG.
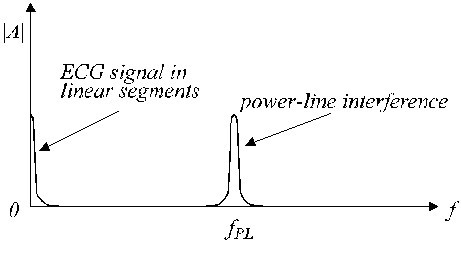
Espectro espectro de frequência aproximado de um segmento linear.
Este critério funciona com precisão, mas dificilmente pode ser aplicado em tempo real porque a sua implementação é relativamente lenta. Este inconveniente é superado por Christov e Dotsinsky que usam um critério modificado de apenas duas diferenças subsequentes.
Cr = | FDi+1- FD i | <M. (3)
A primeira amostra, que não preenche a equação (3), está associada ao início de um segmento não-liner. Na transição não linear para linear, a equação (3) deve ser satisfeita consecutivamente n vezes, a fim de evitar a detecção prematura do segmento linear. O critério é implementado em tempo real para f S = 400 Hz e n = 8,
Later, Dotsinsky e Daskalov definiram o critério como duas diferenças não subseqüentes:
Cr = |FDi+k- FD i | <M, para k >1 (4)
Esta abordagem torna a transição do segmento linear para o não-linear mais precisa.
Compensação das variações de amplitude do PL
Quanto mais frequentemente as correcções são actualizadas, melhor a compensação das variações de amplitude do PL é conseguida. Portanto, o limiar do critério linear, M, tem que ser razoavelmente menos restritivo para que os erros, cometidos através da média de alguns segmentos que se afastam do sinal linear ideal, sejam menores do que os erros, que aparecerão se M iniciar uma atualização esporádica da correção. Inicialmente, M foi fixado em 160 μV . Mais tarde, os valores heurísticos foram encontrados em M = 150 μV e M = 100 μV .
Filtragem linear
Para o número ímpar da amostra n = 2m + 1 em um período da interferência PL, o valor filtrado:
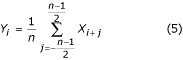
é coincidente em fase com o não filtrado.
No caso do número par n = 2m, os dois valores são desfasados em metade do período amostral:
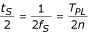
mas tornam-se coincidência na fase usando a fórmula
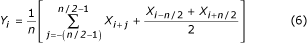
É possível tomar para a média a cada segundo, terceiro ou qthsample se n/q for inteiro. Dependendo se n/q é ímpar ou par, a equação (7) ou (8) é utilizada, respectivamente.

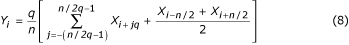
Surge um caso especial de redução máxima da amostra com q = n/2 . A fórmula correspondente:
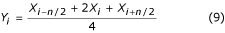
é chamada de filtro de ‘três pontos’. Além da equação (8), a seguinte fórmula
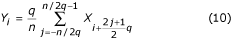
também pode ser aplicada se q for uniforme. No caso de q = n/2, o filtro torna-se ‘dois pontos’ e é representado por:

Número de amostra reduzido em um período da interferência levará a uma inclinação acentuada dos lóbulos do filtro do pente e encurtará o tempo de computação. Contudo, estas ‘vantagens’ devem ser avaliadas cuidadosamente para não violar a regra Nyquist com uma grande quantidade do terceiro harmónico presente. Os outros harmónicos não são tomados em consideração, uma vez que os harmónicos mais altos são normalmente suprimidos por filtros passa-baixo com corte na gama de 100-150 Hz, enquanto os pares estão praticamente ausentes devido à fabricação precisa dos pólos dos geradores da central eléctrica.
Compensação da variação da frequência PL
O desvio permitido da frequência PL nominal é limitado em alguns países até 1% pelos padrões. Na prática, o desvio é muitas vezes maior. Kumaravel et al. relataram uma variação de 3%. McManus et al. encontraram mudanças consideráveis na freqüência de interferência, que é sobreposta aos registros retirados da base de dados dos Padrões Comuns para Eletrocardiografia (CSE).
As variações de freqüência levam a um caso especial de amostragem não-múltipla com n real, ao invés de um inteiro. Esta complicação pode ser contornada se os desvios forem detectados pela medição contínua do hardware de f PL e corrigidos por pequenos ajustes do intervalo de amostragem t S em torno de seu valor nominal (R), t RS = T RPL /n (aqui, T RPL = 20 ms é o T PL nominal para f RPL = 50 Hz). Para f PL , desvio entre 49,5 e 50,1 Hz, as variações t S estão na faixa de 1%, e consequentemente não introduzem erros além da precisão de medição aceita dos parâmetros que são normalmente utilizados para a classificação automática do ECG.
A primeira abordagem associa o disparo de cada primeira amostra, S 1 , das seqüências S k (k = 1, 2…n) nos períodos T PL com amplitude arbitrária escolhida mas constante da tensão PL. As amostras seguintes, S k (k = 2…n), são espaçadas em t S , que é obtido por t S = T RTL /n. Para 50 Hz, e n = 5, t S = 4 ms. Dois tipos de erros cometidos usando esta abordagem são estudados por Dotsinsky e Daskalov . O primeiro, devido a irregularidades entre amostras, pode atingir 1% a f S = 400 Hz e 1,2% a f S = 250 Hz, em caso de desvio de 1% em torno da f RPL . O segundo tipo de erro não excede 3% e é uma consequência da localização adicionalmente deslocada da amostra filtrada.
Dotsinsky e Daskalov relataram uma abordagem melhorada. O período contínuo T PL é medido e dividido por n. O t S obtido é utilizado no T PL subsequente .
Avaliação da eficiência do procedimento
Exemplos de procedimento de subtração são mostrados na Fig. 4 e Fig. 5. Os sinais do ECG são retirados da base de dados da American Heart Association. Os sinais são filtrados para suprimir a interferência de 60 Hz (frequência PL nos EUA). Em seguida, os sinais são misturados com a interferência de 50 Hz, amplitude modulada de 0 a 3,2 mVp-p por uma taxa de variação de 200 μVs-1. Os traços são identificados da seguinte forma: i) sinal de entrada; ii) interferência sintetizada; iii) sinal misto; iv) sinal processado; v) diferença entre sinais originais e processados e vi) diferença ampliada. Na verdade, os componentes descartados incluem também os ruídos eletromiográficos (EMG) e outros ruídos. Uma parte não suprimida do sinal, juntamente com pequenas interferências residuais e distorções devido a comprometimento do valor M também estão presentes nas diferenças.
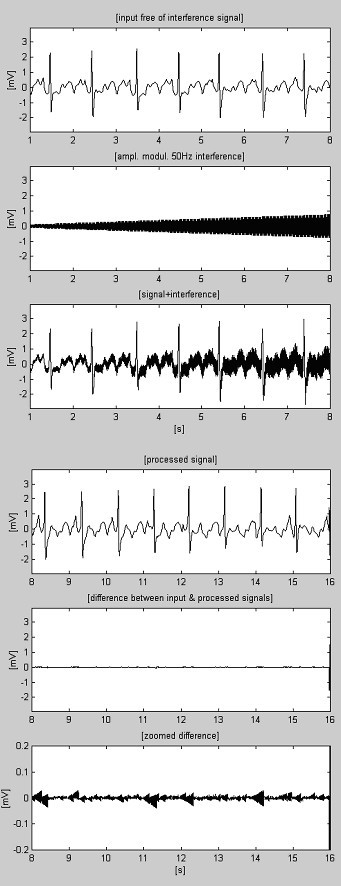
Registro AHA 3004d1 processado.
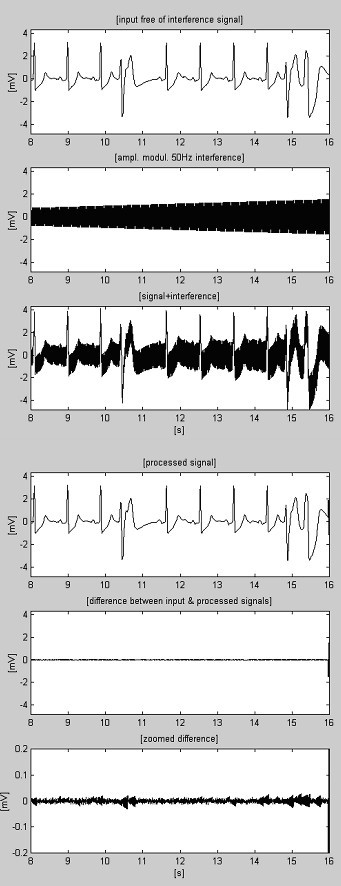
Gravação AHA 6007d1 processada.
Dois sinais são usados para avaliar a eficiência do procedimento de subtracção apenas no que diz respeito à interferência. O primeiro, retirado da nossa própria base de dados, é chamado condicionalmente ‘limpo’ (Fig. 6). O resultado mostra pequenas diferenças entre sinais de entrada e sinais processados, visualmente devido ao ruído apresentado na entrada. Este resultado é verificado com o segundo sinal sintetizado, que não contém quaisquer interferências (Fig. 7). Como pode ser visto, não são introduzidas distorções. O mesmo sinal sintetizado é sobreposto por interferência e processado (Fig. 8). Nenhuma interferência residual pode ser encontrada.
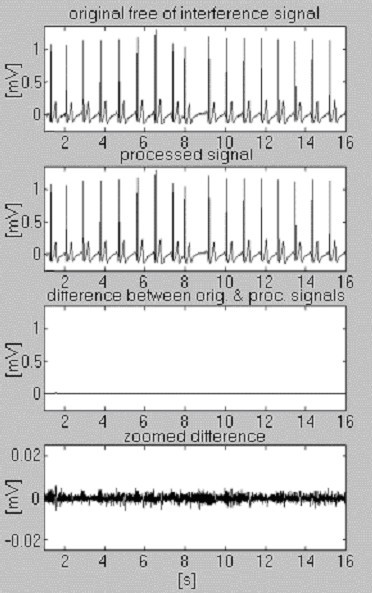
Processamento do sinal condicionalmente ‘limpo’.
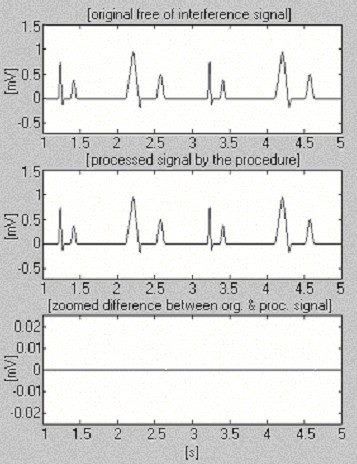
Processamento de sinal sintetizado.
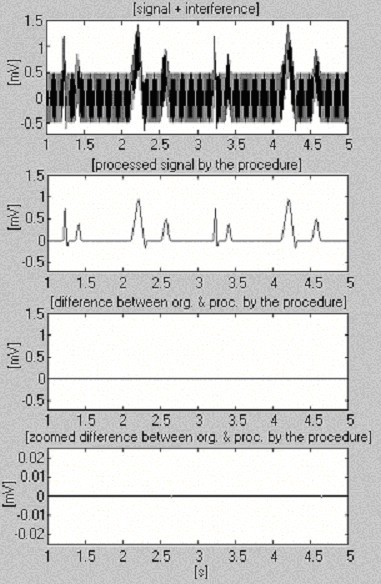
Sinal sintetizado processado+interferência.
Influência do ruído EMG
Por vezes o ruído EMG é tão alto que o achado do segmento linear é dificultado. Como consequência, correções imprecisas, que não correspondem à última alteração da amplitude da interferência, causarão erros (veja o ruído residual entre o 11º e o 14ºs na Fig. 9).
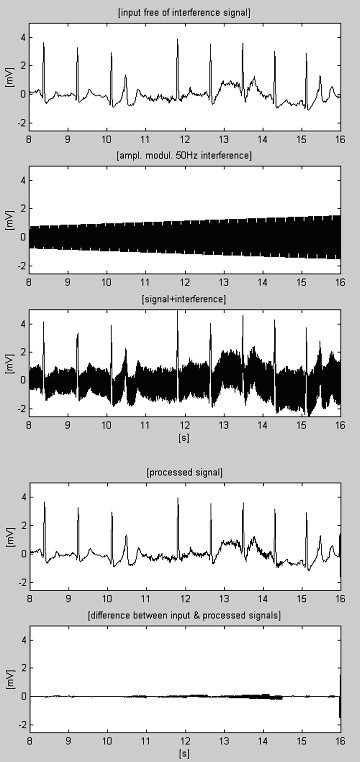
Sinal de ECG processado+ruído EMG+interferência.
Uma abordagem muito simples para a supressão da influência do ruído EMG no procedimento introduz um buffer paralelo adicional onde as porções contínuas do sinal são incondicionalmente calculadas como média. Este buffer é usado para a detecção precisa da linearidade. Fig. 10 e Fig. 11 mostram a comparação dos resultados sem e com o buffer paralelo. Os traços ‘a’ representam o sinal de ECG misturado com interferência e ruído EMG. Os traços ‘b’ na Fig. 10 e ‘c’ na Fig. 11 indicam transições de segmentos lineares para não lineares (funções on-off). Como pode ser visto, a parte do sinal médio na Fig. 10 é muito limitada. Como consequência, a eficiência do procedimento é reduzida (Fig. 10c e 10d. Em contraste, o buffer paralelo permite a detecção de segmentos lineares longos (Fig. 11c e o ruído residual no sinal processado (Fig. 11d é baixo. Entretanto, o ruído não é totalmente suprimido porque uma parte dele participa do cálculo de correção.
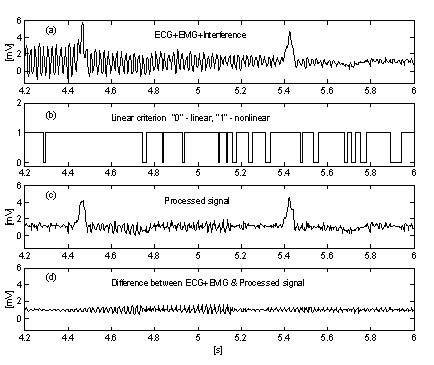
Subtração de interferência+ruído EMG sem buffer paralelo.
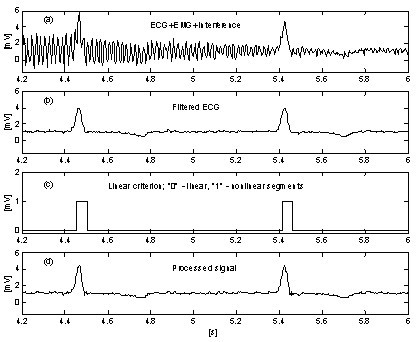
Subtracção de interferência+Ruído EMG com buffer paralelo.
Outra melhora na supressão de ruído EMG é obtida por Christov usando o valor limite adaptativo M, que é calculado com respeito à relação ruído/sinal Rt, definido como Rt = S NL /S F , onde o nível de ruído S NL é igual à largura sumária dos segmentos não lineares em uma época S F , aproximadamente correspondente ao intervalo RR em consideração. A pesquisa de linearidade com um critério de M = 150 μV para ECG ‘limpo’ (Fig. 12a) e para o mesmo sinal, mas contaminado com ruído EMG (Fig. 12b) mostra diferentes S NL , (Fig. 12c e 12d). O método é desenvolvido em ambiente MATLAB. O limiar inicial M é escolhido igual a 30 μV. Em seguida, ele é gradualmente aumentado até Rt atingir 10%, após o qual o procedimento de subtração é iniciado. O valor do nível Rt ≤ 0.1 é sugerido pela razão ‘QRS width versus seu intervalo RR’, que geralmente é em torno de 10%. A eliminação tanto da interferência como do ruído EMG pode ser observada nas Figuras 13b e 13d, onde M = 420 μV é utilizado. Para comparação, o sinal de ECG ‘limpo’ é processado com M = 35 μV (Fig. 13a e 13c).

Níveis de ruído SNL (traços c e d) no sinal de ECG ‘limpo’ (traço a) e no sinal contaminado por EMG (traço b), respectivamente.
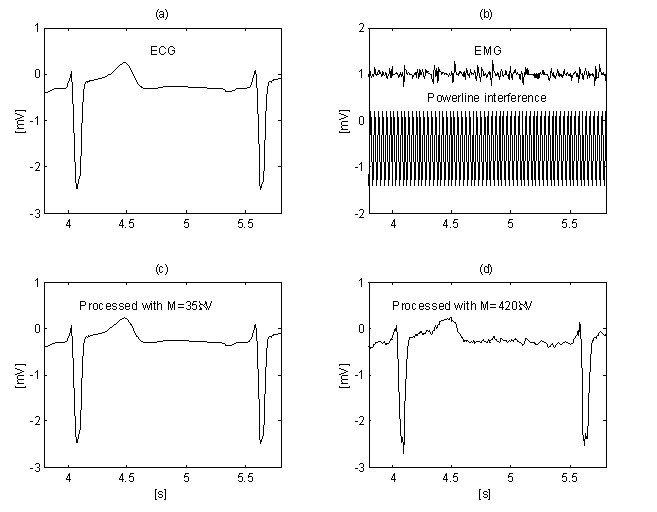
Interferência + supressão de ruído EMG usando limiar adaptativo M: ‘sinal limpo’ (a) processado com M = 35 μV (c) e sinal contaminado (b) submetido ao procedimento com M = 420 μV (d).
Segmentos lineares não podem ser encontrados regularmente em pacientes com fibrilação atrial e ventricular. Entretanto, a preservação total da forma da onda não é necessária para a detecção de fibrilação e, portanto, todos os tipos de filtros tradicionais podem ser aplicados.
Interferência de supressão em ECG de alta resolução
O procedimento de subtração não é diretamente aplicável à superfície do corpo His-ECG, pois a baixa amplitude e a freqüência relativamente baixa His-wave não pode ser distinguida em segmentos lineares. Assim, a His-wave será, na prática, suprimida ou mesmo removida do sinal. O ruído EMG é geralmente de maior amplitude e com um conteúdo de frequência muito mais elevado em comparação com a superfície da His-wave. Portanto, a simples alteração do valor limiar, M, não resulta em delimitação aceitável de segmentos lineares e não lineares.
Bazhina et al. implementaram a seguinte modificação. O início do segmento não-linear detectado antes de um complexo QRS é deslocado 100 ms para a esquerda, definindo assim a região de His-wave como um segmento não-linear por padrão (Fig. 14).
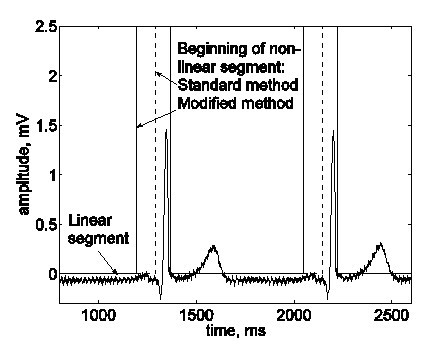
O início de um segmento não-linear incluindo o complexo QRS foi deslocado por padrão 100 ms para a esquerda, para incluir a zona onde se espera que a onda His-bundle apareça.
O procedimento de subtração e outros três métodos: filtros notch, interpolação espectral e subtração de regressão são testados contra distorção mínima do sinal original. A subtração e os procedimentos de regressão-subtração provaram ser os melhores, já que Baratta et al. usam um conceito similar para estimativa de ruído em segmentos lineares. A regressão-subtração trata mal as mudanças de amplitude da interferência dentro do segmento atual.
Caso de dispositivos fornecidos com bateria e sistemas de ECG auxiliados por computador
A medida de hardware de f PL , necessária para compensação da modulação da freqüência de interferência, não é viável em dispositivos fornecidos com bateria e em alguns sistemas de ECG auxiliados por computador. Dotsinsky e Stoyanov estudaram a faixa de mudanças de freqüência de interferência com amplitude constante, para a qual a parte residual é restrita a níveis aceitáveis sem o uso de amostragem sincronizada. Eles descobriram que a interferência residual abaixo de 20 μVp-p poderia ser obtida com o procedimento por: i) amplitude de interferência ≤ 0,4 mVp-p e ii) mudança de freqüência com uma taxa ≤ 0,0125 Hzs-1. Uma vez que tais requisitos para a fonte de alimentação podem frequentemente ser excedidos, foi desenvolvido um software de medição de interferência.
O sinal de ECG é processado inicialmente por um filtro passa-banda de 49-51 Hz. São medidas as amplitudes de duas amostras adjacentes, Br L e Br R , retiradas de uma inclinação positiva da interferência, localizadas abaixo e acima da linha zero (Fig. 15). A distância, t CP , entre o ponto de cruzamento CP e a amostra direita, Br R , é calculada continuamente por:
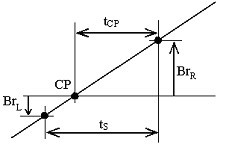
Interferência de cruzamento zero.

Em caso de mudança de T PL, t S é redefinido usando

Esta abordagem foi implementada no ambiente MATLAB. Para frequência de amostragem f S = 500 Hz e f RPL = 50 Hz, n é igual a 10. O produto kn determina o tempo recomendado antes de calcular e substituir o novo tCP,i + knf pelo tCP,i anterior. A figura 16 mostra um sinal de ECG de 1 mV processado após ser misturado por interferência com 2 mVp-p de amplitude constante e extremamente rápido variando em 1 Hz por 8 s de frequência (primeiro traço). Para avaliar a eficiência obtida, também é apresentada a diferença ampliada sem amostragem sincronizada (último traço).
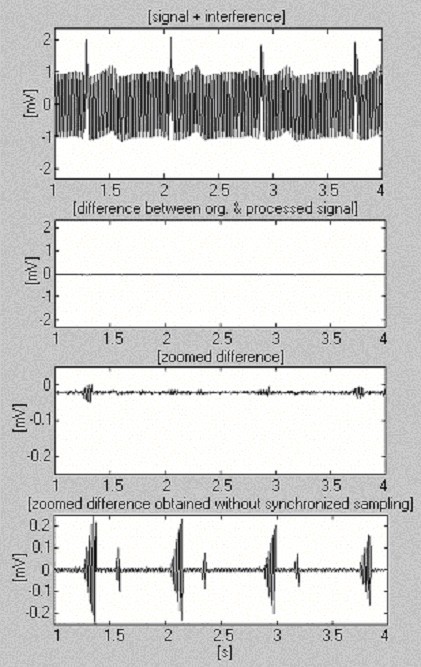
Procedimento de subtração utilizando o software de medição de freqüência da linha de força.
O próximo passo lógico a ser dado consiste em: i) manter a classificação t S do instrumento de ECG, ii) reamostragem do sinal de acordo com o PL medido em curso, a fim de eliminar a interferência e iii) retorno à classificação t S . Os primeiros resultados de tal abordagem são altamente promissores . Assim, a compensação do software da variável f PL , bem como uma implementação total do procedimento de subtração em um instrumento, incluindo o ajuste automático para f RPL de 50 ou 60 Hz, será concluída, independentemente dos circuitos de hardware e do software correspondente.
A adaptação automática à freqüência nominal do PL
Um programa comum para subtração alternativa de interferência em ambiente de 50 e 60 Hz leva a uma amostragem não múltipla, ou seja, a n. Valores largamente utilizados de t S para f RPL = 50 Hz, tais como 250, 500 e 1000 Hz, correspondem a n irracional de 4.1(6), 8.3(3) e 4.1(6) se a interferência de 60 Hz tiver que ser eliminada. No caso inverso, f S = 360 Hz requer n = 7,2. Valores arredondados n* são inaceitáveis de usar, pois eles introduziriam um erro considerável.
Uma solução muito simples que não precisa de f S alteração foi encontrada por Dotsinsky e Stoyanov . O procedimento original aplica um filtro de pente ao longo de um período, T PL , da interferência. Assim, o programa corre mais rápido. Geralmente, n pode ser retirado de k > 1 períodos inteiros. O procedimento é operado se:
n = kT PL /t S é um número inteiro.
Para t S = 2 ms (f S = 500 Hz) e f RPL = 50 Hz, o menor valor de k satisfatório (14) é realmente k = 1. No entanto, no caso de 60 Hz, k é igual a 3. Zeros associados com as sub-harmonicas 20 e 40 Hz também aparecerão, mas não têm influência no procedimento. Portanto, é suficiente trocar n entre 10 (k = 1) e 25 (k = 3) para operar com ambas as interferências. Para este efeito, dois filtros passa-banda digitais verificam o sinal de entrada. A figura 17 mostra que o filtro com banda de frequência sobreposta à interferência gera um sinal de saída de magnitude superior ao do outro filtro.
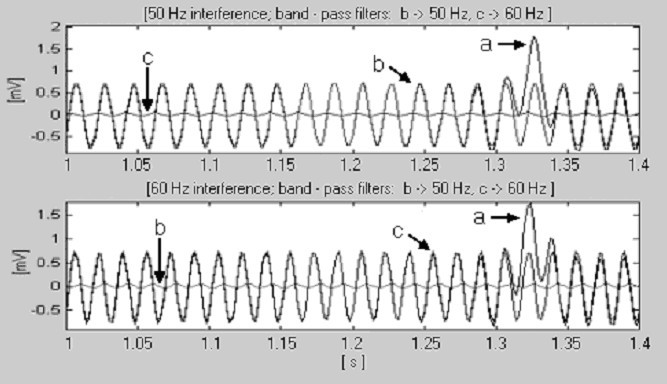
Detecção da frequência nominal da linha de potência, a) parte do complexo QRS, b) interferência de 50 Hz e c) interferência de 60 Hz.
Desenvolvimento do procedimento teórico
A teoria do procedimento de subtracção foi desenvolvida por Mihov , Levkov e Mihov , e Mihov et al. Eles propuseram quatro tipos de filtros, implementados em uma estrutura generalizada que pode superar os problemas com quase todos os casos de amostragem não-múltipla, incluindo variações de freqüência de interferência, sem utilizar a conversão AD sincronizada.
O chamado filtro D na amostragem múltipla é definido como Cr na equação (2), onde a segunda diferença, D i , é obtida com FD s que estão espaçados em um T PL :
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
A função de transferência do filtro D tem zeros a f = 0 e f = f PL Hz, que é mostrado igual a 50 Hz na figura. 18,
 >
>Função de transferência do filtro D para fPL = 50 Hz.
O filtro K descreve a média móvel apresentada pelas equações (5) e (6). Sua função de transferência é dada na Fig. 19 para n = 5 em caso de multiplicidade ímpar.
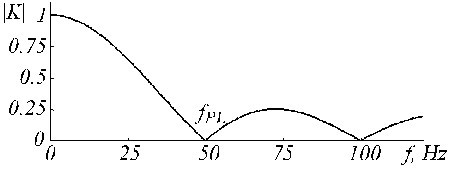
Função de transferência do filtro K para fPL = 50 Hz e n = 5.
A equação usada para o cálculo contínuo dos componentes de interferência:
B i = X i – Y i (16)
Filtro digital chamado (1-K)-filtro.
Outras vezes, os filtros são redefinidos para amostragem não múltipla, e f S = 250 Hz em conjunto com f RPL = 60 Hz é levado em consideração para ilustrar a melhoria do software.
Para preservar a função de transferência zeros, o filtro D tem que ser subtraído com um filtro de correção com zero em f = 0 e ganho de D RPL em f = f RPL , igual ao ganho do filtro D para a mesma freqüência, f RPL . A síntese do filtro de correção é baseada em um filtro auxiliar de três pontos dado pela equação:

onde (n/2)* é o valor arredondado de n/2.
Desde que A RPL é o ganho do filtro auxiliar para f = f RPL , o filtro de correção é multiplicado pela razão D RPL /A RPL . Usando as funções de transferência correspondentes, D RPL e A RPL são computados antecipadamente por:
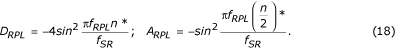
Finalmente, o filtro D* corrigido é apresentado como

e é mostrado na Fig. 20 pelo traço ‘c’, onde traços ‘a’ e ‘b’ são o filtro D-filtro e o filtro de correção, respectivamente.
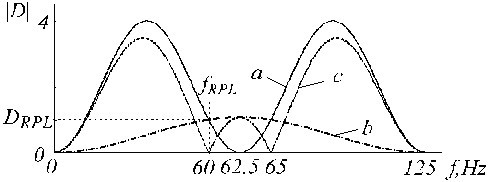
Funções de transferência de a) Filtro D, b) filtro auxiliar de correção e c) filtro D corrigido.
A função de transferência do filtro K deve preservar zero para f = f RPL , ganho unitário para f = 0 e resposta de fase linear. O procedimento de correção do filtro K é similar ao anterior. Um filtro auxiliar é dado pela fórmula usada para o cálculo das correções:
A i = X i – Y i , (20)
O ganho do filtro é igual a 1 – K RPL para f = f RPL , onde K RPL é o ganho do filtro K para a mesma freqüência f RPL . O filtro auxiliar é multiplicado por K RPL /(1 – K RPL ) e subtraído do filtro K. A equação para o filtro K* corrigido é:
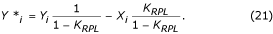
A constante K RPL pode ser estimada por:

para multiplicidade ímpar ou uniforme, respectivamente.
Um exemplo de correção do filtro K é mostrado na Fig. 21, onde traços ‘a’, ‘b’ e ‘c’ representam o filtro K primário, o filtro auxiliar, e o filtro K* corrigido.
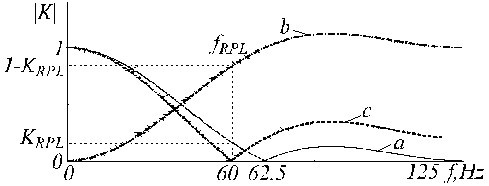
Função de transferência de a) filtro K, b) filtro auxiliar de correção e c) filtro K corrigido.
No caso de amostra não múltipla, aparece uma diferença de fase entre as amostras de ECG em curso e os componentes de interferência B i (equação 16) geralmente localizados em um buffer temporário first-in-first-out (FIFO). Portanto, o B i deve ser modificado sendo subtraído das amostras de ECG durante segmentos não lineares. O procedimento de compensação é relativamente complicado. A figura 22 mostra o conteúdo do tampão temporário. A amostra de interferência atual, B i-n *, não coincide com a amostra restaurada, B i . Sua amplitude deve ser recalculada a fim de compensar a diferença de fase entre elas. Isto é realizado por um novo filtro com resposta de fase linear e ganho de unidade para f = f RPL , denotado como o filtro B. Ele é sintetizado a partir do conhecido filtro K, com uma janela igual ao período de interferência. No caso de n* ímpar, pode ser descrito como:
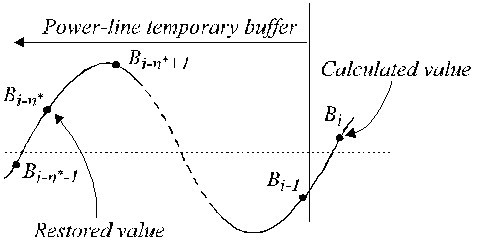
Valores restaurados no buffer temporário.
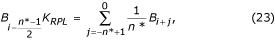
onde K RPL é o ganho para a interferência do filtro de média dada pela equação (22).
O valor do tampão B i restaurado pode ser calculado por:
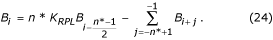
Em caso de n*:
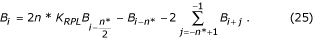
A função de transferência do filtro B é mostrada na figura. 23.
 >
>Funções de transferência do a) filtro B e b) do conhecido filtro K.
A estrutura generalizada é apresentada na Fig. 24, onde os módulos do procedimento de subtração são os seguintes:
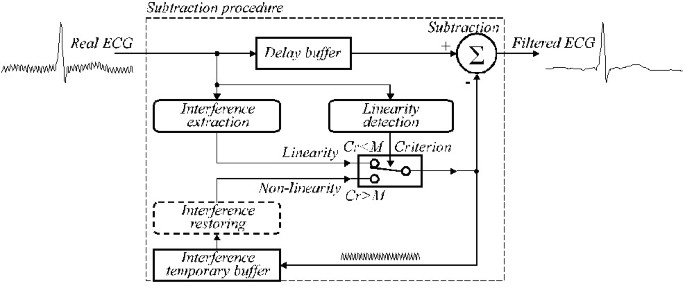
Estrutura generalizada do procedimento de subtração.
-
Detecção de linearidade. O filtro D é aplicado para avaliar a linearidade da vizinhança de cada amostra de sinal.
-
Extracção de interferências. (1-K)-filtro é usado para calcular o componente de interferência.
-
Critério. A condição Cr <M envia ou a interferência PL extraída ou restaurada para Subtração.
-
Buffer temporário de interferência. O componente de interferência extraído ou restaurado usado como correção em segmento não-linear é salvo na posição bloqueada com a fase em andamento da interferência da linha de alimentação.
-
Interferência restaurada. O filtro B é chamado em caso de amostragem não multipla para restaurar os valores de correção verdadeiros, que devem ser subtraídos das amostras de sinal de entrada em segmentos não-lineares.
-
Tampão de retardo. Compensa o atraso, que aparece com o filtro D e (1-K)-filtro e é imperativo se o procedimento for executado em tempo quase-real. Caso contrário, o buffer poderia ser desconsiderado.
-
Subtração. O valor da interferência extraído ou restaurado é subtraído do sinal de entrada retardado para a saída do sinal de ECG ‘limpo’. Em caso de não-linearidade tanto a extração de interferência quanto a subtração implementam o filtro K.
Um algoritmo melhorado de acordo com a estrutura generalizada foi testado off-line. Os resultados para f S = 250 Hz e f RPL = 60 Hz são mostrados na Fig. 25.
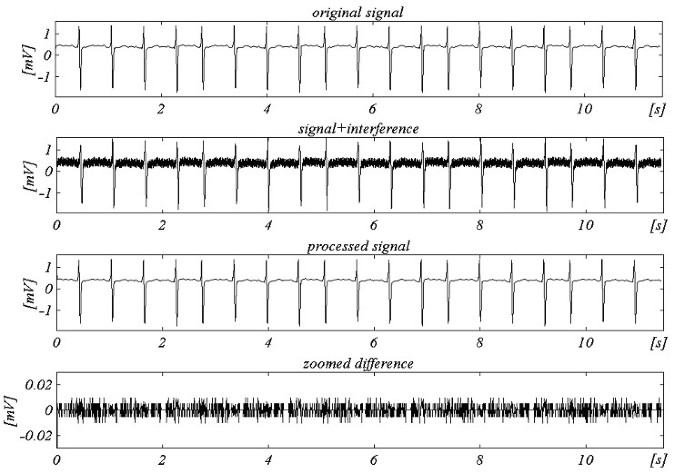
Exemplo para amostragem não múltipla com fRPL = 60 Hz e fS = 250 Hz.