Veja os artigos recentes

Abstract

Light travels through a vacuum at speed c regardless of the motion of the light source or that of an observer’s frame of reference. Consequentemente, é necessário algum tempo para que a luz viaje de uma fonte de luz para um observador no espaço, de forma que a emissão de luz e a observação da luz emitida não sejam simultâneas. Com base nestas considerações, é proposto um método para medir a velocidade absoluta de um observador, que poderia ser utilizado para determinar o estado de movimento de uma nave espacial a partir do interior de uma cabine fechada. Neste estudo, uma nova explicação da transformação de Lorentz também é introduzida.

Palavras-chave

sistema de coordenadas, sistema de referência, movimento, velocidade absoluta, relatividade, transformação de Lorentz, tempo, espaço, observador, fonte de luz
A análise seguinte apresenta uma abordagem prática para medir a velocidade absoluta de um observador, que poderia ser usada para determinar o estado de movimento de uma nave espacial a partir do interior de uma cabine fechada. O conceito de velocidade absoluta refere-se geralmente a uma velocidade uniforme padrão dos vários objetos de um sistema físico em relação a um espaço imóvel postulado que existe independentemente dos objetos físicos contidos nele (ou seja, um espaço absoluto). Apresentamos aqui uma abordagem baseada em cinemáticas rígidas para demonstrar que a velocidade absoluta de um observador pode ser determinada a partir do facto de a luz viajar através de um vácuo à velocidade c independentemente do movimento da fonte de luz ou do quadro de referência de um observador. Consequentemente, é necessário algum tempo para que a luz viaje de uma fonte de luz para um observador no espaço, de modo que a emissão de luz e a observação da luz emitida não sejam simultâneas.
Na análise proposta, fornecemos primeiro as seguintes convenções para os sistemas de coordenadas em consideração. Assumimos um sistema de coordenadas cartesianas composto por três pares de eixos perpendiculares com origem no ponto (0,0,0), onde qualquer ponto P no espaço pode ser definido pelas suas coordenadas ao longo dos eixos x, y e z, representados por um par ordenado de números reais (x,y,z). Um sistema de referência inercial S é assumido como representado por um sistema de coordenadas retangulares do espaço (x,y,z) cuja origem é O. Uma série de relógios padrão (denominados relógios S) estão localizados em pontos estacionários em S. Os relógios S são calibrados mutuamente (ou seja, fornecem leituras equivalentes no mesmo instante no tempo) com base na transmissão e recepção de um sinal luminoso. Especificamente, no tempo tA, um feixe de luz é projetado do relógio A para o relógio B, que é então refletido no tempo tB pelo relógio B de volta para o relógio A, e chega no relógio A no tempo tA’. Se , os dois relógios são calibrados. Para qualquer evento localizado nas coordenadas x,y,z, sua coordenada de tempo t é dada pela leitura do relógio S relacionado ao evento. Da mesma forma, outro sistema de referência inercial S’ é estabelecido com base num segundo sistema de coordenadas rectangulares espaciais (x’,y’,z’) cuja origem é O’, e uma outra série de relógios padrão calibrados mutuamente (relógios S’) estão localizados em pontos estacionários do sistema de referência S’. Para qualquer evento localizado nas coordenadas x’,y’,z’, a sua coordenada temporal t’ é dada pela leitura do relógio S’ relacionado com o evento.
Porque as respectivas origens das coordenadas espaciais e temporais, bem como as direcções dos eixos de coordenadas podem ser seleccionadas arbitrariamente em grande medida, as relações entre S e S’ aqui empregues baseiam-se nas seguintes convenções, que foram aplicadas para simplificar.
(1) Num determinado instante, as origens e coordenadas dos dois sistemas são sobrepostas, e os relógios localizados respectivamente em O e O’ são colocados a zero, ou seja .
(2) Os eixos x e x’ são coincidentes na direcção do movimento relativo de S e S’; assim, x e x’ são sempre coincidentes, enquanto y e y’, assim como z e z’ são paralelos.
(3) S’ move-se na direcção +x de S.
A análise proposta baseia-se no princípio fundamental de que a luz num vácuo viaja a uma velocidade constante c, independentemente do movimento do observador ou da fonte de luz. Assim, definimos aqui a velocidade absoluta U do observador, que se assume ser linear e uniforme, como , onde f(φ) representa uma função da relação geométrica entre a direcção de um sinal luminoso e a direcção de U, aqui designada como φ.
Duas novas explicações sobre a relatividade do tempo e do comprimento são fornecidas na análise proposta, que diferem das explicações de Einstein (ver “On the Electrodynamics of Moving Bodies”). Estas explicações são introduzidas nas secções seguintes.

A relatividade do tempo

Devido à velocidade finita da luz, é necessário algum tempo para a luz viajar de uma fonte de luz para um observador no espaço. Pode-se portanto deduzir que a emissão de luz e a observação da luz não podem ser simultâneas. Com base na constância da velocidade da luz e nas condições ilustradas na Figura 1, definimos os seguintes factores. As posições de uma fonte de luz e de um observador a , momento em que a fonte de luz emite luz (indicado como evento R), são dadas respectivamente como A e H0. Durante o período de propagação da luz de a , o observador percorre uma distância U∙T da posição H0 a H, onde o observador recebe a luz emitida. Assim, definimos como a distância l entre a posição do observador ao receber o sinal luminoso em e a posição da fonte luminosa ao emitir a luz em . Devido à constância da velocidade da luz, . A distância é equivalente a U∙T. Finalmente, definimos como a distância l0 entre a posição do observador a e a posição da fonte de luz a . Aqui, introduzimos uma consideração da posição do observador em , que anteriormente se pensava não ter qualquer significado físico. Se os estados de movimento do observador e da fonte de luz forem equivalentes, é dado l0, de modo que U pode ser calculado através das relações triangulares ilustradas na Figura 1.
No presente trabalho, o tempo de um evento é medido utilizando o seguinte método. Tanto o observador como um relógio são colocados na origem. Quando o sinal luminoso que representa a ocorrência de um evento chega ao observador, a hora de chegada da luz corresponderá à hora indicada pelo relógio. A vantagem da correspondência é que ela está sempre relacionada com a posição do observador que emprega o relógio. Como visto na Figura 1, o ponto espacial O3 pode ser definido com base na posição da fonte luminosa ao emitir luz a , e o ponto espacial O2 pode ser definido com base na posição do observador ao receber luz a . Contudo, o meio de definir o ponto espacial O1 no qual o observador se encontra quando a fonte de luz emite luz a , não é óbvio. Para resolver este problema, são introduzidos os conceitos de repouso absoluto (ou seja, ) e movimento absoluto (ou seja, ). Substituímos respectivamente o observador em movimento único em H0 e H por dois observadores H1 e H2 em repouso nos pontos espaciais O1 e O2, respectivamente, enquanto a fonte de luz A está em repouso no ponto espacial O3. Cada um dos observadores e a fonte de luz empregam relógios padrão calibrados, e A emite um sinal luminoso a , denotado como evento R0. Quando o observador H1 recebe o sinal luminoso viajando em c, a leitura do relógio é T0, e quando H2 recebe, a leitura é T. Como tal, as distâncias e podem ser definidas com base nos respectivos tempos de viagem do sinal luminoso da seguinte forma:
, (1)
e
. (2)
De acordo com as relações triangulares mostradas na Figura 1, a transformação do evento R0 entre os observadores H1 e H2 é dada da seguinte forma:
(3)
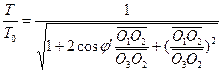(4)
Aqui, é o ângulo entre a linha O3O1 e o eixo x, e é o ângulo entre a linha O3O2 e o eixo x.
Retornando agora à condição de um único observador em movimento, assumimos que, no sistema S, tanto o observador H como a fonte luminosa A empregam um relógio padrão calibrado. No instante do evento R, a fonte de luz A está no ponto espacial O3, e o observador H está em O1. O instante em que o sinal luminoso atinge o ponto espacial O1 corresponde a uma leitura de relógio S de T0. Quando o observador H recebe o sinal luminoso, a leitura é T, e H está em O2.
Obtendo o curso, H não pode observar o evento R no ponto O1. Para resolver este problema, outro observador H-é colocado no sistema S no ponto O1 correspondendo com , onde a posição de H- é empregada para definir o ponto espacial O1. Então, a transformação do evento R entre os observadores H- e H pode ser obtida através da Equação (3) da seguinte forma.
(5)
Hence, Equações (3) e (4) podem ser reescritas da seguinte forma.
(6)
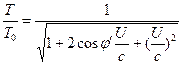(7)
e observe também que, para , as Equações (6) e (7) simplificam para o seguinte.
(8)
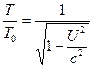(9)
Por isso, com base na análise acima, um método simples de determinação de U pode ser obtido da Equação (6), dado que (φ) é conhecido.
Para efeitos de simplicidade, uma fonte de luz com um estado de movimento equivalente ao dos observadores é escolhida como quadro de referência. Um observador é colocado no centro de uma barra rígida reta em movimento linear uniforme, e os sinais luminosos de diferentes posições na barra chegam ao observador em momentos diferentes. O observador detecta a deflexão da barra na posição do observador com um ângulo de deflexão que pode ser obtido a partir da Equação (8).
Por este método, o estado de movimento de uma nave espacial pode ser determinado a partir de uma cabine fechada.

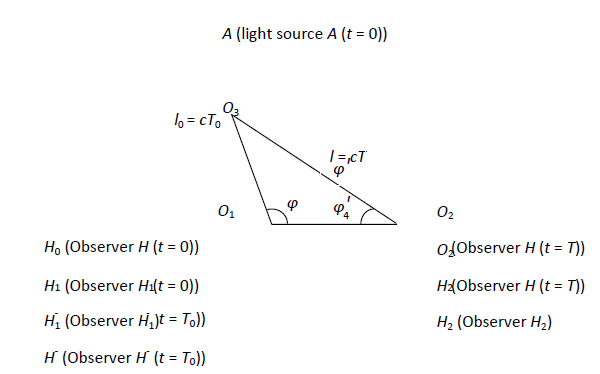
Figure 1: estados de movimento do observador e da fonte de luz

A relatividade do comprimento

Na análise acima, dois comprimentos foram introduzidos, ou seja, e . Neste caso, consideramos o comprimento de uma barra que se assume ser uma barra rígida estacionária de comprimento L dentro do seu sistema de coordenadas, para o qual L é medido com uma mira estacionária, e onde o eixo da barra é coincidente com o eixo x de um sistema de coordenadas que se desloca com movimento linear uniforme no sentido +x a uma velocidade absoluta U. Assume-se que L é determinado pelas duas operações definidas abaixo.
(a) O observador reside no mesmo sistema de coordenadas em movimento que o calibre da barra e da mira, e L é medido por sobreposição do calibre da barra e da mira.
(b) Com a ajuda de vários relógios posicionados em coordenadas estacionárias, que se movem em sincronização, o observador mede as posições das duas extremidades da barra em coordenadas estacionárias num momento específico t, e a distância entre as duas posições é medida com o calibre da mira estacionária. é o comprimento calculado a partir da operação (a), que é aqui indicado como o comprimento da barra na coordenada em movimento. é o comprimento calculado a partir da operação (b), que é aqui indicado como o comprimento de uma barra em movimento na coordenada estacionária. É óbvio que e são diferentes.
Anos supomos que, no sistema S, o observador H- está no mesmo estado de movimento que H. Então, como mostrado na Figura 1, H- está no ponto O1 quando recebe o sinal luminoso em , e, simultaneamente, o observador H está no ponto O4. Portanto, t=0,04
é a distância entre H- e H a , e
. (10)
é a distância percorrida pelo observador H no intervalo de T0 a T, de modo que
. (11)
é a distância entre H- em e H em , tal que
. (12)
Assim, pode-se deduzir a seguinte expressão.
(13)
Próximo, vamos considerar as transformações de coordenadas e tempo entre dois sistemas de coordenadas em movimento, ambos se movem com uma velocidade linear uniforme, o que representa uma nova explicação da transformação de Lorentz.
Assumindo que o observador H (no sistema S), o observador H’ (no sistema S’), e a fonte de luz A” (no sistema S”) empregam relógios padrão calibrados individualmente, e, em , a fonte de luz A” emite um sinal luminoso, denotado como evento R”. No instante do evento R”, A” está no ponto O3, e os observadores H e H” são coincidentes. Quando o observador H recebe o sinal luminoso, a leitura do relógio S é T, e H está no ponto O1. Quando o observador H’ recebe o sinal luminoso, a leitura do relógio S é o T’, e H’ está no ponto O2. Então, a transformação do evento R” entre os observadores H’ e H pode ser calculada a partir da Equação (3), onde
. (14)
Here, u é a velocidade relativa entre os observadores H’ e H, que produz as seguintes transformações.
(15)
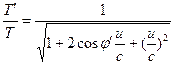(16)
De , as seguintes relações podem ser derivadas:
. (17)
Quando e , a Equação (16) simplifica para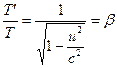
. (18)
Por isso, as seguintes relações de transformação podem ser deduzidas:
, (19)
, (20)
, (21)
. (22)
Mais, quando ,
, (23)
e
, (24)
, (25)
, (26)
. (27)