Consultați articolele recente

Abstract

Lumina călătorește în vid cu viteza c, indiferent de mișcarea sursei de lumină sau de cea a cadrului de referință al observatorului. În consecință, este necesar un anumit timp pentru ca lumina să călătorească de la o sursă de lumină până la un observator în spațiu, astfel încât emisia de lumină și observarea luminii emise nu sunt simultane. Pe baza acestor considerații, se propune o metodă de măsurare a vitezei absolute a unui observator, care ar putea fi utilizată pentru a determina starea de mișcare a unei nave spațiale din interiorul unei cabine închise. În acest studiu, se introduce, de asemenea, o nouă explicație a transformării Lorentz.

Cuvintele cheie

sistem de coordonate, sistem de referință, mișcare, viteză absolută, relativitate, transformarea Lorentz, timp, spațiu, observator, sursă de lumină
Analiza de mai jos prezintă o abordare practică pentru măsurarea vitezei absolute a unui observator, care ar putea fi utilizată pentru determinarea stării de mișcare a unei nave spațiale din interiorul unei cabine închise. Conceptul de viteză absolută se referă, în general, la o viteză uniformă standard a diferitelor obiecte ale unui sistem fizic în raport cu un spațiu imobil postulat care există independent de obiectele fizice conținute în el (adică un spațiu absolut). În acest articol, prezentăm o abordare bazată pe cinematica rigidă pentru a demonstra că viteza absolută a unui observator poate fi determinată pornind de la faptul că lumina călătorește prin vid cu viteza c, indiferent de mișcarea sursei de lumină sau de cea a cadrului de referință al observatorului. În consecință, este necesar un anumit timp pentru ca lumina să călătorească de la o sursă de lumină până la un observator în spațiu, astfel încât emisia de lumină și observarea luminii emise nu sunt simultane.
În analiza propusă, oferim mai întâi următoarele convenții pentru sistemele de coordonate luate în considerare. Presupunem un sistem de coordonate carteziene alcătuit din trei axe perpendiculare perechi cu originea în punctul (0,0,0), unde orice punct P din spațiu poate fi definit prin coordonatele sale de-a lungul axelor x, y și z, reprezentate de o pereche ordonată de numere reale (x,y,z). Se presupune că un sistem de referință inerțial S este reprezentat de un sistem de coordonate spațiale dreptunghiulare (x,y,z) a cărui origine este O. O serie de ceasuri standard (denumite „ceasuri S”) sunt amplasate în puncte staționare din S. Ceasurile S sunt calibrate reciproc (adică furnizează citiri echivalente în același moment de timp) pe baza transmiterii și recepționării unui semnal luminos. Mai exact, la momentul tA, un fascicul de lumină este proiectat de la ceasul A la ceasul B, care este apoi reflectat la momentul tB de către ceasul B înapoi spre ceasul A și ajunge la ceasul A la momentul tA’. Dacă , cele două ceasuri sunt calibrate. Pentru orice eveniment situat la coordonatele x,y,z, coordonata de timp t a acestuia este dată de citirea ceasului S legat de eveniment. În mod similar, un alt sistem de referință inerțial S’ este stabilit pe baza unui al doilea sistem de coordonate dreptunghiulare spațiale (x’,y’,z’) a cărui origine este O’, iar o altă serie de ceasuri standard calibrate reciproc (ceasurile S’) sunt amplasate în puncte staționare în sistemul de referință S’. Pentru orice eveniment situat la coordonatele x’,y’,z’, coordonata sa temporală t’ este dată de citirea ceasului S’ legat de eveniment.
Pentru că originile respective ale coordonatelor spațiale și temporale, precum și direcțiile axelor de coordonate pot fi alese în mare măsură în mod arbitrar, relațiile dintre S și S’ utilizate aici se bazează pe următoarele convenții, care au fost aplicate pentru simplitate.
(1) La un anumit moment în timp, originile și axele de coordonate ale celor două sisteme sunt suprapuse, iar ceasurile situate la O și, respectiv, O’ sunt setate la zero, și anume, .
(2) Axele x și x’ sunt coincidente în direcția mișcării relative a lui S și S’; astfel, x și x’ coincid în orice moment, în timp ce y și y’, precum și z și z’ sunt paralele.
(3) S’ se deplasează de-a lungul direcției +x a lui S.
Analiza propusă se bazează pe principiul fundamental că lumina în vid se deplasează cu o viteză constantă c, indiferent de mișcarea observatorului sau a sursei de lumină. Astfel, definim aici viteza absolută U a observatorului, care este presupusă a fi liniară și uniformă, ca , unde f(φ) reprezintă o funcție a relației geometrice dintre direcția unui semnal luminos și direcția lui U, notată aici ca φ.
Două noi explicații ale relativității timpului și a lungimii sunt oferite în analiza propusă, care diferă de explicațiile lui Einstein (vă rugăm să vă referiți la „Despre electrodinamica corpurilor în mișcare”). Aceste explicații sunt prezentate în următoarele secțiuni.

Relativitatea timpului

Datorită vitezei finite a luminii, este necesar un anumit timp pentru ca lumina să călătorească de la o sursă de lumină până la un observator din spațiu. Prin urmare, se poate deduce că emisia de lumină și observarea luminii nu pot fi simultane. Pe baza constanței vitezei luminii și a condițiilor ilustrate în figura 1, se definesc următorii factori. Pozițiile unei surse de lumină și a unui observator la , moment în care sursa de lumină emite lumină (notat ca eveniment R), sunt date de A și, respectiv, H0. În timpul perioadei de propagare a luminii de la la , observatorul parcurge o distanță U∙T de la poziția H0 la H, în urma căreia observatorul primește lumina emisă. În consecință, definim ca fiind distanța l dintre poziția observatorului la primirea semnalului luminos la și poziția sursei de lumină în momentul emiterii luminii la . Datorită constanței vitezei luminii, . Distanța este echivalentă cu U∙T. În sfârșit, definim ca fiind distanța l0 dintre poziția observatorului la și poziția sursei de lumină la . Aici, introducem o considerație privind poziția observatorului la , despre care se credea anterior că nu are nicio semnificație fizică. Dacă stările de mișcare ale observatorului și ale sursei de lumină sunt echivalente, l0 este dat, astfel încât U poate fi calculat prin intermediul relațiilor triunghiulare ilustrate în ,figura 1.
În lucrarea de față, timpul unui eveniment este măsurat folosind următoarea metodă. Atât observatorul cât și un ceas sunt plasate la origine. Atunci când semnalul luminos care reprezintă apariția unui eveniment ajunge la observator, ora de sosire a luminii va corespunde cu ora indicată de ceas. Avantajul acestei corespondențe este că ea este întotdeauna legată de poziția observatorului care utilizează ceasul. După cum se vede în figura 1, punctul spațial O3 poate fi definit pe baza poziției sursei de lumină atunci când emite lumină la , iar punctul spațial O2 poate fi definit pe baza poziției observatorului atunci când primește lumina la . Cu toate acestea, mijloacele de definire a punctului spațial O1 la care se află observatorul atunci când sursa de lumină emite lumină la nu sunt evidente. Pentru a rezolva această problemă, se introduc conceptele de repaus absolut (de exemplu, ) și mișcare absolută (de exemplu, ). Înlocuim observatorul unic în mișcare de la H0 și H cu doi observatori H1 și H2 aflați în repaus în punctele spațiale O1 și, respectiv, O2, în timp ce sursa de lumină A este în repaus în punctul spațial O3. Fiecare dintre observatori și sursa de lumină utilizează ceasuri standard calibrate, iar A emite un semnal luminos la , notat ca eveniment R0. Când observatorul H1 primește semnalul luminos care se deplasează cu c, citirea ceasului este T0, iar când îl primește H2, citirea este T. Astfel, distanțele și pot fi definite pe baza timpilor de deplasare respectivi ai semnalului luminos, după cum urmează:
, (1)
și
. (2)
Conform relațiilor triunghiulare prezentate în figura 1, transformarea evenimentului R0 între observatorii H1 și H2 este dată după cum urmează:
(3)
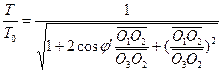(4)
Aici, este unghiul dintre linia O3O1 și axa x, iar este unghiul dintre linia O3O2 și axa x.
Returnându-ne acum la condiția unui singur observator în mișcare, presupunem că, în sistemul S, atât observatorul H, cât și sursa de lumină A utilizează un ceas etalon calibrat. În momentul evenimentului R, sursa de lumină A se află în punctul spațial O3, iar observatorul H se află în O1. Momentul în care semnalul luminos ajunge în punctul spațial O1 corespunde cu o citire a ceasului S de T0. În momentul în care observatorul H primește semnalul luminos, citirea este T, iar H se află la O2.
Desigur, H nu poate observa evenimentul R în punctul O1. Pentru a rezolva această problemă, un alt observator H- este plasat în sistemul S în punctul O1 care corespunde cu , unde poziția lui H- este folosită pentru a defini punctul spațial O1. Apoi, transformarea evenimentului R între observatorii H- și H poate fi obținută prin ecuația (3) după cum urmează.
(5)
În consecință, Ecuațiile (3) și (4) pot fi rescrise după cum urmează:
(6)
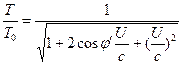(7)
e observă, de asemenea, că, pentru , Ecuațiile (6) și (7) se simplifică în felul următor.
(8)
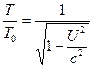(9)
Prin urmare, pe baza analizei de mai sus, se poate obține o metodă simplă de determinare a lui U din Ecuația (6), având în vedere că (φ) este cunoscută.
Pentru simplificare, se alege ca cadru de referință o sursă de lumină cu o stare de mișcare echivalentă cu cea a observatorilor. Un observator este plasat în centrul unei bare rigide drepte în mișcare liniară uniformă, iar semnalele luminoase din diferite poziții de pe bară ajung la observator în momente diferite. Observatorul detectează devierea barei în poziția observatorului cu un unghi de deviere care poate fi obținut din ecuația (8).
Prin această metodă, starea de mișcare a unei nave spațiale ar putea fi determinată dintr-o cabină închisă.

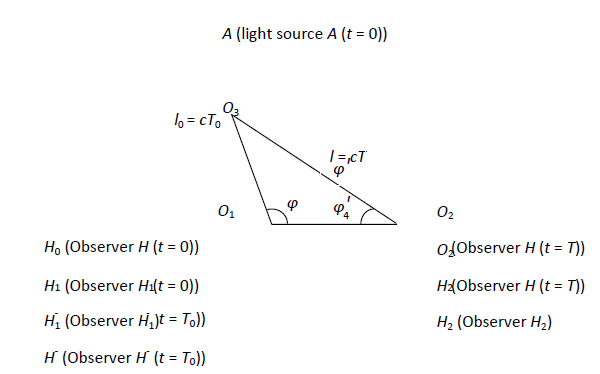
Figura 1: stările de mișcare ale observatorului și ale sursei de lumină

Relativitatea lungimii

În analiza de mai sus, au fost introduse două lungimi, și anume și . În acest caz, se consideră lungimea unei bare despre care se presupune că este o bară rigidă staționară de lungime L în cadrul sistemului său de coordonate, pentru care L se măsoară cu un etalon staționar și în care axa barei coincide cu axa x a unui sistem de coordonate care se deplasează cu o mișcare liniară uniformă pe direcția +x cu o viteză absolută U. Se presupune că L se determină prin cele două operații definite mai jos.
(a) Observatorul locuiește în același sistem de coordonate în mișcare ca și bara și rigla, iar L se măsoară prin suprapunerea barei și a riglei.
(b) Cu ajutorul mai multor ceasuri poziționate în coordonate staționare, care se mișcă în sincronizare, observatorul măsoară pozițiile celor două capete ale barei în coordonate staționare la un anumit moment t, iar distanța dintre cele două poziții se măsoară cu rigla staționară. este lungimea calculată din operația (a), care este notată aici ca lungimea barei în coordonate mobile. este lungimea calculată din operația (b), care este notată aici ca lungime a barei în mișcare în coordonatele staționare. Este evident că și sunt diferite.
Să presupunem că, în sistemul S, observatorul H- se află în aceeași stare de mișcare ca și H. Atunci, așa cum se arată în figura 1, H- se află în punctul O1 atunci când primește semnalul luminos la , iar, simultan, observatorul H se află în punctul O4. Prin urmare, t=0,04
este distanța dintre H- și H la , iar
. (10)
este distanța parcursă de observatorul H în intervalul de la T0 la T, astfel încât
. (11)
este distanța dintre H- la și H la , astfel încât
. (12)
Ca atare, se poate deduce următoarea expresie.
(13)
În continuare, vom considera transformările de coordonate și de timp între două sisteme de coordonate în mișcare, ambele mișcându-se cu o viteză liniară uniformă, ceea ce reprezintă o nouă explicație a transformării lui Lorentz.
Să presupunem că observatorul H (în sistemul S), observatorul H’ (în sistemul S’) și sursa de lumină A” (în sistemul S”) utilizează toate individual ceasuri standard calibrate și, la , sursa de lumină A” emite un semnal luminos, notat ca eveniment R”. În momentul evenimentului R”’, A” se află în punctul O3, iar observatorii H și H’ sunt coincidenți. În momentul în care observatorul H primește semnalul luminos, citirea ceasului S este T, iar H se află în punctul O1. Când observatorul H’ primește semnalul luminos, citirea ceasului S’ este T’, iar H’ se află în punctul O2. Apoi, transformarea evenimentului R”’ între observatorii H’ și H poate fi calculată din ecuația (3), unde
. (14)
Aici, u este viteza relativă între observatorii H’ și H, ceea ce conduce la următoarele transformări.
(15)
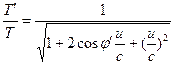(16)
Din , se pot obține următoarele relații:
. (17)
Când și , ecuația (16) se simplifică la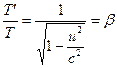
. (18)
Prin urmare, se pot deduce următoarele relații de transformare:
, (19)
, (20)
, (21)
. (22)
Mai mult, când ,
, (23)
și
, (24)
, (25)
, (26)
. (27)