Convoluțiile 2D și 3D explicate cu… MS Excel!

Am început cu convoluțiile 2D în prima postare deoarece convoluțiile au câștigat o popularitate semnificativă după succesele din domeniul Computer Vision. Deoarece sarcinile din acest domeniu folosesc imagini ca intrări, iar imaginile naturale au, de obicei, modele de-a lungul a două dimensiuni spațiale (de înălțime și lățime), este mai frecvent să vedem exemple de convoluții 2D decât de convoluții 1D și 3D.

Mai recent, însă, a existat un număr foarte mare de succese în aplicarea convoluțiilor și în sarcinile de procesare a limbajului natural. Deoarece sarcinile din acest domeniu utilizează text ca intrări, iar textul are modele de-a lungul unei singure dimensiuni spațiale (adică timpul), convoluțiile 1D se potrivesc de minune! Le putem utiliza ca alternative mai eficiente la rețelele neuronale recurente (RNN) tradiționale, cum ar fi LSTM și GRU. Spre deosebire de RNN-uri, ele pot fi rulate în paralel pentru calcule foarte rapide.

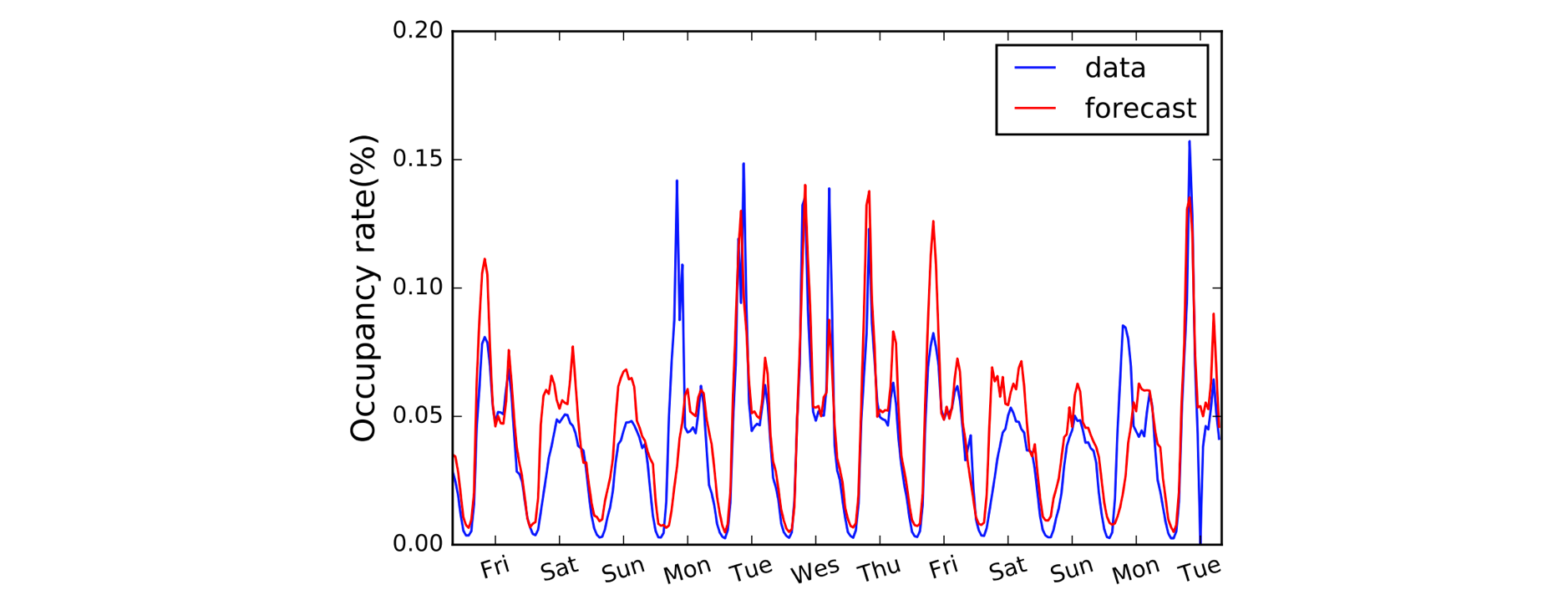
Un alt domeniu care beneficiază de Convoluțiile 1D este modelarea seriilor temporale. Ca și înainte, avem o singură dimensiune spațială pe datele noastre de intrare (adică timpul) și dorim să preluăm modele pe perioade de timp. Adesea numim acest tip de date „secvențiale”, deoarece pot fi privite ca o secvență de valori. Iar dimensiunea spațială o numim adesea dimensiunea „temporală”. Utilizarea convoluțiilor 1D înaintea RNN-urilor este, de asemenea, destul de frecventă: modelul LSTNet este un exemplu în acest sens, iar predicțiile sale pentru prognoza traficului sunt prezentate mai jos.

A, B, C. Este simplu ca (1,3,3) punct (2,0,1) = 5.

După ce convențiile de denumire au fost clarificate, haideți acum să ne uităm mai atent la aritmetică. Suntem norocoși, deoarece convoluțiile 1D sunt de fapt doar o versiune simplificată a convoluției 2D!

Lucrând cu calculul unei singure valori de ieșire, putem aplica nucleul nostru de mărime 3 la regiunea de mărime echivalentă din partea stângă a matricei noastre de intrare. Calculăm „produsul în puncte” al regiunii de intrare și al nucleului, care, pentru a recapitula, este doar produsul element-înțelept (adică înmulțirea perechilor de culori) urmat de o sumă globală pentru a obține o singură valoare. Deci, în acest caz:

(1*2) + (3*0) + (3*1) = 5

Aplicăm aceeași operație (cu același nucleu) la celelalte regiuni ale matricei de intrare pentru a obține matricea de ieșire completă de (5,6,7,2); adică glisăm nucleul pe întreaga matrice de intrare. Spre deosebire de convoluțiile 2D, unde glisăm nucleul în două direcții, pentru convoluțiile 1D glisăm nucleul doar într-o singură direcție; stânga/dreapta în această diagramă.

Avansat: o convoluție 1D nu este același lucru cu o convoluție 1×1 2D.

Codarea lucrurilor

În mod surprinzător, vom avea nevoie de un bloc Conv1D în Gluon pentru convoluția noastră 1D. Definim forma nucleului ca fiind 3 și, din moment ce lucrăm doar cu un singur nucleu în acest exemplu, vom specifica channels=1.

import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)

Acum putem trece intrarea noastră în blocul conv folosind un nucleu predefinit.

input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>

Ce se schimbă cu padding, stride și dilatare?

Am văzut efectul padding, stride și dilatare în ultima postare despre convoluțiile 2D și este foarte similar pentru convoluțiile 1D. În ceea ce privește padding-ul, de data aceasta vom face pad doar de-a lungul unei singure dimensiuni (dimensiunea temporală). Diagrama noastră reprezintă timpul de-a lungul axei orizontale, așa că facem pad la stânga și la dreapta datelor de intrare (și nu deasupra și dedesubt ca în exemplul Convoluției 2D). Cu stride și dilatare, le aplicăm doar de-a lungul dimensiunii temporale, de asemenea. Așadar, un exemplu cu padding și stride ar arăta după cum urmează:

Aducem două argumente suplimentare în cod: padding=1 și strides=2.

conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>

Avansat: dimensiunile datelor de intrare trebuie să se conformeze unei anumite ordini numite layout. În mod implicit, convoluția 1D se așteaptă să fie aplicată datelor de intrare în formatul „NCW”, adică dimensiunea lotului (N) * canale (C) * lățime/timp (W). Iar pentru convoluțiile 2D, valoarea implicită este „NCHW”, adică dimensiunea lotului (N) * canale (C) * înălțime (H) * lățime (W). Verificați argumentul layout din Conv1D și Conv2D.

.