Grup abelian | CDhistory

DOWNLOAD Mathematica Notebook

Un grup abelian este un grup pentru care elementele se comută (i.e., pentru toate elementele și ). Grupurile abeliene corespund, prin urmare, grupurilor cu tabele de înmulțire simetrice.

Toate grupurile ciclice sunt abeliene, dar un grup abelian nu este neapărat ciclic. Toate subgrupurile unui grup abelian sunt normale. Într-un grup abelian, fiecare element se află într-o clasă de conjugare de sine stătătoare, iar tabelul de caractere implică puteri ale unui singur element cunoscut sub numele de generator de grup.

În limbajul Wolfram, funcția AbelianGroup reprezintă produsul direct al grupurilor ciclice de grade , , ….

Nu se cunoaște o formulă generală pentru a da numărul de grupuri finite neisomorfe de un anumit ordin de grup. Cu toate acestea, numărul de grupuri finite abeliene neisomorfe de ordinul al oricărui grup dat este dat prin scrierea sub forma

(1)

unde sunt factori primi distincți, atunci

(2)

unde este funcția de partiție, care este implementată în limbajul Wolfram ca FiniteAbelianGroupCount. Valorile lui pentru , 2, … sunt 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 3, 2, … (OEIS A000688).

Cele mai mici ordine pentru care există , 2, 3, … grupuri abeliene neisomorfe sunt 1, 4, 8, 36, 16, 72, 32, 900, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), unde 0 reprezintă un număr imposibil (adică nu este un produs de numere de partiții) de grupuri Abeliene neisomorfe. Valorile „lipsă” sunt 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Cele mai mari numere incrementale de grupuri abeliene în funcție de ordin sunt: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), care apar pentru ordinele 1, 4, 8, 16, 32, 64, 128, 256, 512, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

Teorema de descompunere a lui Kronecker afirmă că orice grup abelian finit poate fi scris ca un produs direct de grupuri ciclice de ordinul grupurilor de putere primă. Dacă ordinul de grup al unui grup finit este un prim , atunci există un singur grup abelian de ordin (notat ) și nici un grup neabelian. Dacă ordinul grupului este un număr prim la pătrat , atunci există două grupuri abeliene (notate și . Dacă ordinul grupului este un număr prim cubic , atunci există trei grupuri abeliene (notate , și ), și cinci grupuri în total. Dacă ordinul este un produs a două numere prime și , atunci există exact un grup abelian de ordinul (notat ).

Un alt rezultat interesant este că dacă denotă numărul de grupuri abeliene neisomorfe de ordinul grupului , atunci

(3)

unde este funcția zeta Riemann.

Numele grupurilor abeliene de ordine sunt date de 1, 2, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 19, 20, 25, … (OEIS A063966) pentru , 2, …. Srinivasan (1973) a arătat, de asemenea, că

(4)

unde

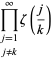			(5)
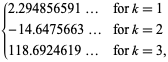			(6)

(OEIS A021002, A084892, și A084893) și este din nou funcția zeta Riemann. Rețineți că Richert (1952) a dat incorect . Sumele pot fi, de asemenea, scrise în formele explicite