Intervale de toleranță
Această secțiune conține detalii statistice pentru intervale de toleranță unilaterale și bilaterale.
Intervale bazate pe distribuția normală
Intervalul unilateral
Intervalul unilateral se calculează după cum urmează:
Limita inferioară = 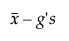
Limita superioară = 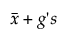
unde
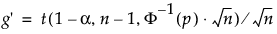
s este abaterea standard
t este cuantilul de la noncentrală a distribuției t
Φ-1 este cuantila normală standard
Intervalul bilateral
Intervalul bilateral se calculează după cum urmează:
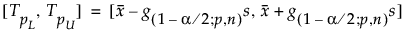
unde s este abaterea standard și g(1-α/2; p,n) este o constantă.
Pentru a determina g, considerați fracțiunea din populație captată de intervalul de toleranță. Tamhane și Dunlop (2000) dau această fracție după cum urmează:
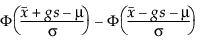
unde Φ denotă cdf (funcția de distribuție cumulativă) normală standard.
În consecință, g rezolvă următoarea ecuație:
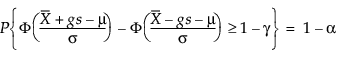
unde 1 – γ este fracțiunea tuturor observațiilor viitoare conținute în intervalul de toleranță.
Pentru mai multe informații despre intervalele de toleranță bazate pe distribuția normală, a se vedea tabelele J.1a, J.1b, J.6a și J.6b din Meeker et al. (2017).
Intervale neparametrice
Limita inferioară unilaterală
Limita inferioară de toleranță unilaterală 100(1 – α)% pentru a conține cel puțin o proporție β din distribuția eșantionată dintr-un eșantion de dimensiune n este statistica de ordin x(l). Indicele l se calculează după cum urmează:
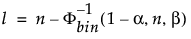
unde Φ-1bin(1-α, n, β) este cel de-al (1 – α)-lea cuantile al distribuției binomiale cu n încercări și probabilitatea de succes β.
Nivelul real de încredere se calculează ca Φbin(n-l, n, β), unde Φbin(x, n, β) este probabilitatea ca o variabilă aleatoare distribuită binomial cu n încercări și probabilitatea de succes β să fie mai mică sau egală cu x.
Rețineți că pentru a calcula un interval inferior de toleranță unilaterală fără distribuție unilaterală, dimensiunea eșantionului n trebuie să fie cel puțin la fel de mare ca 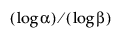 .
.
Limita superioară unilaterală
Limita superioară de toleranță unilaterală 100(1 – α)% pentru a conține cel puțin o proporție β din distribuția eșantionată dintr-un eșantion de dimensiune n este statistica de ordine x(u). Indicele u se calculează după cum urmează:
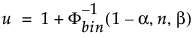
unde Φ-1bin(1-α, n, β) este al (1 – α)-lea cuantile al distribuției binomiale cu n încercări și probabilitatea de succes β.
Nivelul de încredere real se calculează ca Φbin(u-1, n, β), unde Φbin(x, n, β) este probabilitatea ca o variabilă aleatoare distribuită binomial cu n încercări și probabilitatea de succes β să fie mai mică sau egală cu x.
Rețineți că pentru a calcula un interval de toleranță superior unilateral fără distribuție, dimensiunea eșantionului n trebuie să fie cel puțin la fel de mare ca 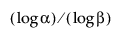 .
.
Intervalul de toleranță bilaterală
Intervalul de toleranță bilaterală de 100(1 – α)% pentru a conține cel puțin o proporție β din distribuția eșantionată dintr-un eșantion de dimensiune n se calculează după cum urmează:
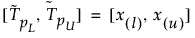
unde x(i) este statistica de ordinul i-lea, iar l și u se calculează după cum urmează:
Să ν = n – Φ-1bin(1-α, n, β), unde Φ-1bin(1-α, n, β) este al (1 – α)-lea cuantile al distribuției binomiale cu n încercări și probabilitatea de succes β. În cazul în care ν este mai mic de 2, nu se poate calcula un interval de toleranță fără distribuție bilaterală. Dacă ν este mai mare sau egal cu 2, l = floor(ν/2) și u = floor(n + 1 – ν/2).
Nivelul de încredere real se calculează ca Φbin(u-l-1, n, β), unde Φbin(x, n, β) este probabilitatea ca o variabilă aleatoare distribuită binomial cu n încercări și probabilitatea de succes β să fie mai mică sau egală cu x.
Rețineți că, pentru a calcula un interval de toleranță fără distribuție bilaterală, dimensiunea eșantionului n trebuie să fie cel puțin la fel de mare ca n din următoarea ecuație:

Pentru mai multe informații despre intervalele de toleranță fără distribuție, a se vedea Meeker et al. (2017, sec. 5.3).
.