Reconstituire 3D

În această practică, se intenționează să se programeze logica necesară pentru a permite robotului kobuki să genereze o reconstrucție 3D a scenei pe care o recepționează prin intermediul camerelor sale din stânga și din dreapta.

Instalare

Instalează infrastructura generală a Academiei de Robotică JdeRobot.

Cum să vă executați soluția?

Navigați în directorul 3d_reconstruction

cd exercises/3d_reconstruction

Lansează Gazebo cu lumea kobuki_3d_reconstruction prin comanda

roslaunch ./launch/3d_reconstruction_ros.launch

Apoi trebuie să execuți aplicația academică, care va încorpora codul tău:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Cum se execută exercițiul?

Pentru a realiza exercițiul, trebuie să editați fișierul MyAlgorithm.py și să inserați în el codul dumneavoastră, care reconstruiește punctele 3d din cele două vederi stereo.

Unde se introduce codul?

În fișierul MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Interfața de programare a aplicației

• self.getImage('left') – pentru a obține imaginea din stânga
• self.getImage('right') – pentru a obține imaginea din dreapta
• self.point.PlotPoint(position, color) – pentru a trasa punctul în instrumentul 3d

Navigația în interfața GUI

Bazată pe mouse: Țineți apăsat și trageți pentru a vă deplasa în mediul înconjurător. Derulați pentru a mări sau micșora imaginea

Bazat pe tastatură: Tastele săgeată pentru a vă deplasa în mediul înconjurător. Tastele W și S pentru a mări sau micșora imaginea

Teorie

În domeniul vederii computerizate și al graficii computerizate, reconstrucția 3D este procesul de determinare a profilului 3D al unui obiect, precum și de cunoaștere a coordonatelor 3D ale oricărui punct de pe acest profil. Reconstrucția poate fi realizată după cum urmează:

• Bazat pe hardware: Abordarea bazată pe hardware ne cere să utilizăm hardware-ul specific sarcinii de reconstrucție. Utilizarea luminii structurate, a telemetrului laser, a radiometrului de adâncime și a metodelor radiometrice sunt câteva exemple.

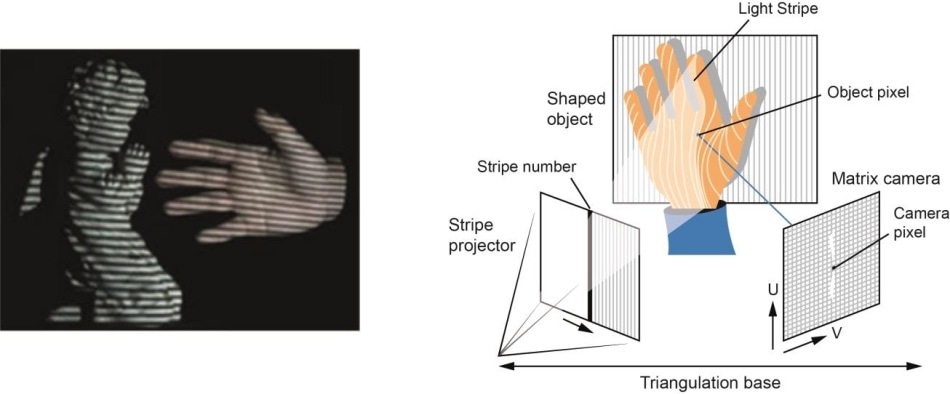
• Software Based: Abordarea bazată pe software se bazează pe capacitățile de calcul ale computerului pentru a determina proprietățile 3D ale obiectului. Forma din umbrire, textura, viziunea stereo și omografia sunt câteva metode bune.

În acest exercițiu, scopul nostru principal este de a realiza reconstrucția 3D folosind o abordare bazată pe software, în special reconstrucția 3D prin viziune stereo.

Geometrie epipolară

Când două camere de luat vederi vizualizează o scenă 3D din două poziții diferite, există o serie de relații geometrice între punctele 3D și proiecțiile lor pe imaginile 2D care conduc la constrângeri între punctele imaginii. Studiul acestor proprietăți și constrângeri se numește Geometrie epipolară. Imaginea și explicația de mai jos pot generaliza ideea:

Să presupunem că un punct X din spațiul 3d este imaginat în două vederi, la x în prima și x' în a doua. Retroproiectând razele spre centrele lor de cameră prin planurile imaginii, obținem o suprafață plană, notată cu π.

Supunând acum că știm doar x, ne putem întreba cum este constrâns punctul corespunzător x'. Planul π este determinat de linia de bază(linia care unește centrele camerelor de luat vederi) și de raza definită de x. Din cele de mai sus, știm că raza corespunzătoare punctului necunoscut x' se află în π, prin urmare punctul x' se află pe linia de intersecție l' a lui π cu al doilea plan al imaginii. Această dreaptă se numește dreaptă epipolară corespunzătoare lui x. Această relație ne ajută să reducem spațiul de căutare a punctului din imaginea din dreapta, de la un plan la o dreaptă. Câteva definiții importante de reținut sunt:

• Epipolul este punctul de intersecție a dreptei care unește centrele camerei (linia de bază) cu planul imaginii.

• Un plan epipolar este un plan care conține linia de bază.

• O linie epipolară este punctul de intersecție a planului epipolar cu planul imaginii.

Reconstrucția stereo

Reconstrucția stereo este un caz special al reconstrucției 3d de mai sus, în care cele două planuri ale imaginii sunt paralele între ele și la aceeași distanță față de punctul 3d pe care dorim să îl reprezentăm.

În acest caz, linia epipolară pentru ambele planuri de imagine este aceeași și este paralelă cu lățimea planurilor, simplificând mai bine constrângerea noastră.

Algoritm de reconstrucție 3D

Algoritmul de reconstrucție constă în 3 etape:

Să le analizăm pe rând

Detectarea punctelor caracteristice

Detectarea punctelor caracteristice este un domeniu vast de studiu în care sunt deja studiați mai mulți algoritmi. Algoritmii Harris Corner Detection și Shi-Tomasi folosesc valorile proprii pentru a obține un punct caracteristic bun. Dar, problema este că avem nevoie de o mulțime de puncte pentru reconstrucția 3D, iar acești algoritmi nu vor putea să ne ofere un număr atât de mare de puncte caracteristice.

De aceea, folosim punctele de margine ca puncte caracteristice. Este posibil să existe o ambiguitate în detectarea lor în următoarea etapă a algoritmului. Dar, problema noastră este rezolvată prin luarea marginilor ca puncte caracteristice. Un detector de margini foarte interesant este Algoritmul Canny Edge Detection. Algoritmul este destul de simplu și fiabil în ceea ce privește generarea marginilor.

Feature Point Extraction

Utilizarea constrângerii epipolare simplifică într-adevăr complexitatea în timp a algoritmului nostru. Pentru problemele generale de reconstrucție 3d, trebuie să generăm o linie epipolară pentru fiecare punct dintr-un cadru de imagine și apoi să căutăm în acel spațiu de eșantionare punctul corespunzător din celălalt cadru de imagine. Generarea liniei epipolare este, de asemenea, foarte ușoară în cazul nostru, fiind vorba doar de iterpolarea liniei paralele din planul imaginii din stânga în planul imaginii din dreapta.

Verificarea corespondenței dintre imagini implică mulți algoritmi, cum ar fi suma diferențelor pătratice sau minimizarea energiei. Fără a intra prea mult în profunzime, utilizarea unui simplu filtru de corelație este, de asemenea, suficientă pentru cazul nostru de utilizare.

Triangulație

Triangulația, în termeni simpli, este doar calcularea locului în care se va afla punctul 3d folosind cele două puncte determinate în planurile imaginii.

În realitate, poziția punctelor imaginii nu poate fi măsurată cu exactitate. În cazul camerelor foto generale, pot exista distorsiuni geometrice sau fizice. Prin urmare, în spatele minimizării acestei erori și a calculării celei mai exacte proiecții a punctelor 3d se află o mulțime de matematică. Consultați acest link pentru un model simplu.

Sugestii

Sugestii simple furnizate pentru a vă ajuta să rezolvați exercițiul 3d_reconstruction. Biblioteca OpenCV este folosită intensiv pentru acest exercițiu.

Setup

Utilizând API-ul exercițiului, putem prelua cu ușurință imaginile. De asemenea, după obținerea imaginilor, este o idee bună să efectuăm o filtrare bilaterală a imaginilor, deoarece există unele detalii suplimentare care nu trebuie să fie incluse în timpul reconstrucției 3d. Consultați ilustrațiile pentru a vedea efectele efectuării filtrării bilaterale.

Calcularea corespondențelor

OpenCV are deja filtre de corelație încorporate, care pot fi apelate prin matchTemplate(). Aveți grijă de cazurile extreme, cum ar fi marginile și colțurile.

O observație bună este că punctele din stânga vor avea corespondență în partea stângă, iar punctele din dreapta vor avea corespondență în partea dreaptă. Folosind această observație, putem accelera cu ușurință calculul corespondenței.

Plotarea punctelor

Funcția manuală sau cea bazată pe OpenCV triangulatePoints funcționează bine pentru triangulație. Aveți grijă doar de toate formele și dimensiunile matricelor în timp ce efectuați implementările algebrice.

Rețineți diferența dintre coordonatele 3D simple și coordonatele 4D omogene. Consultați acest videoclip pentru detalii. Simpla împărțire a vectorului 4d complet la a 4-a coordonată a acestuia ne dă coordonatele 3d.

Datorită implementărilor variate ale utilizatorilor, este posibil ca utilizatorul să fie nevoit să ajusteze scara și decalajul punctelor triangulate pentru a le face vizibile și reprezentabile în interfața GUI. Reducerea scării vectorului de coordonate 3D cu o valoare cuprinsă între 500 și 1000 funcționează bine. De asemenea, un decalaj de la 0 la 8 funcționează bine.

Ilustrații

.