Subtraktiomenetelmä PL:n poistamiseksi kehitettiin ensimmäisen kerran noin kaksi vuosikymmentä sitten . Tämä menettely ei vaikuta PL-taajuuden viereisiin EKG-komponentteihin. Tämä teoreettinen tutkimus on tehty PL:n perustaajuudelle, mutta johtopäätökset pätevät myös sen harmonisille taajuuksille ja näin ollen mielivaltaiselle häiriöaaltomuodolle. Menettelyn tehokkuus ei riipu häiriön amplitudista, kunhan vahvistin ei ole kyllästynyt. Lisäksi menettely selviää onnistuneesti häiriön amplitudin ja taajuuden muutoksista. Menettelyä on vuosien mittaan jatkuvasti parannettu, ja se on otettu käyttöön tuhansissa EKG-laitteissa ja tietokoneavusteisissa järjestelmissä. Myös muut tutkijat ovat julkaisseet samankaltaisia lähestymistapoja.
- PERIAATTEET
- Lineaarinen kriteeri
- PL:n amplitudivaihteluiden kompensointi
- Lineaarinen suodatus
- PL-taajuuden vaihtelun kompensointi
- Menettelyn tehokkuuden arviointi
- EMG-kohinan vaikutus
- Häiriöiden vaimentaminen korkean resoluution EKG:ssä
- Paristokäyttöisten laitteiden ja tietokoneavusteisten EKG-järjestelmien tapaus
- Automaattinen sovitus nimelliselle PL-taajuudelle
- Teoreettisen menettelyn kehittäminen
PERIAATTEET
Subtraktiomenetelmää sovelletaan alun perin näytteenottotaajuudella f S , joka on moninkertainen PL-taajuuden f PL kanssa ja laitteisto synkronoitu siihen. Menettely koostuu seuraavista vaiheista :
-
ECG-segmentit, joiden taajuuskaista on lähellä nollaa, havaitaan jatkuvasti käyttäen sopivaa kriteeriä. Niitä kutsutaan lineaarisiksi segmenteiksi, ja niitä esiintyy pääasiassa PQ- ja TP-väleissä, mutta myös R- ja T-aaltojen riittävän pitkissä suorissa osissa.
-
Näytteet näistä segmenteistä keskiarvoistetaan liukuvasti eli niille tehdään lineaarinen vaihekammiosuodatin, jonka ensimmäinen nollakohta on asetettu tasolle f PL . Näin suodatetut näytteet eivät sisällä interferenssiä.
-
Interferenssiamplitudit, joita kutsutaan korjauksiksi, lasketaan kullekin PL-jakson T PL vaihelukitulle näytteelle n vähentämällä suodatetut näytteet saastuneen (alkuperäisen) EKG-signaalin vastaavista näytteistä.
-
Saatujen korjausten joukko päivitetään jatkuvasti lineaarisissa segmenteissä ja sitä käytetään epälineaarisissa segmenteissä (tavallisesti QRS-kompleksien ja suuramplitudisten T-aaltojen ympärillä) häiriön vähentämiseksi alkuperäisestä EKG-signaalista.
Yksi ensimmäisistä subtraktiomenetelmällä saaduista tuloksista on esitetty kuvassa 1 . Häiriö lisättiin puhtaaseen simuloituun EKG-signaaliin menetelmän virheiden ja tehokkuuden arvioimiseksi.
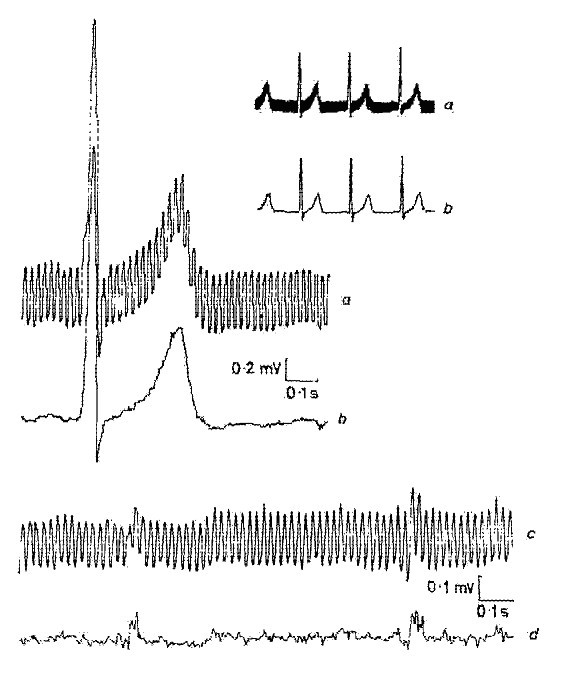
Yksi ensimmäisistä subtraktiomenetelmällä saaduista tuloksista.
Lineaarinen kriteeri
Lineaarinen kriteeri, Cr, vastaa yleensä signaalin toista erotusta (lineaarisuuden matemaattinen arviointi). Ensimmäinen Cr määritellään seuraavasti. Kuusi peräkkäistä ensimmäistä eroa, FD i , lasketaan käyttäen signaalinäytteitä, X i , jotka ovat yhden T PL:n välein :
FD i = X i+n – X i , varten i = 1 … 6 (1)
PL:n interferenssi ensimmäisissä eroissa vaimenee, jos n = f S /f PL . Tässä tapauksessa n = 5, koska menettely kehitettiin alun perin nimellisille f PL = 50 Hz ja f S = 250 Hz. Lisäksi Cr:
Cr = | FD max – FD min | <M, (2)
jossa M on kynnysarvo.
Tyypilliset lineaariset ja epälineaariset segmentit on esitetty kuvassa 2. Todellinen EKG-signaali (jälki a) on päällekkäin interferenssin kanssa (jälki b). Lineaariset segmentit sisältävät matalataajuisen signaalin ja voimalinjan taajuuskomponentit. Tällaisten lineaaristen segmenttien likimääräinen taajuusspektri on esitetty kuvassa 3.

Tyypillisiä lineaarisia ja epälineaarisia segmenttejä todellisessa EKG-signaalissa.
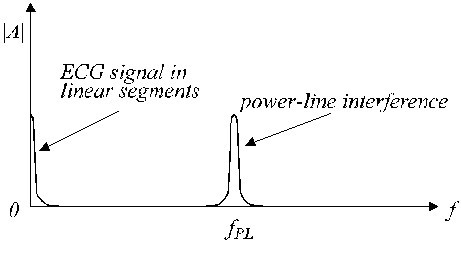
Lineaarisen segmentin likimääräinen taajuusspektri.
Kriteeri toimii tarkasti, mutta sitä tuskin pystytään soveltamaan tosiaikana, koska sen toteutus on suhteellisen hidas. Tämän epäkohdan poistavat Christov ja Dotsinsky, jotka käyttävät muokattua kriteeriä, jossa on vain kaksi peräkkäistä eroa.
Cr = | FDi+1- FD i | <M. (3)
Ensimmäinen näyte, joka ei täytä yhtälöä (3), liittyy ei-liner-segmentin alkuun. Ei-lineaarisesta lineaariseksi siirtymässä yhtälön (3) pitäisi täyttyä peräkkäin n kertaa, jotta vältettäisiin lineaarisen segmentin ennenaikainen havaitseminen. Kriteeri on toteutettu reaaliajassa f S = 400 Hz:lle ja n = 8:lle.
Myöhemmin Dotsinsky ja Daskalov määrittelivät kriteerin kahtena ei-peräkkäisenä erona:
Cr = |FDi+k- FD i | <M, kun k >1 (4)
Tämän lähestymistavan avulla siirtyminen lineaarisesta segmentistä epälineaariseen segmenttiin saadaan tarkemmaksi.
PL:n amplitudivaihteluiden kompensointi
Mitä useammin korjauksia päivitetään, sitä paremmin PL:n amplitudivaihtelut kompensoidaan. Tämän vuoksi lineaarisen kriteerin kynnysarvon M on oltava kohtuullisesti vähemmän rajoittava, jotta virheet, jotka aiheutuvat joidenkin ihanteellisesta lineaarisesta signaalista poikkeavien segmenttien keskiarvoistamisesta, ovat pienempiä kuin virheet, joita syntyy, jos M käynnistää korjauksen satunnaisen päivittämisen. Aluksi M oli 160 μV . Myöhemmin todettiin heuristisiksi arvoiksi M = 150 μV ja M = 100 μV .
Lineaarinen suodatus
Parittomalla näytemäärällä n = 2m + 1 yhdessä PL-interferenssin jaksossa suodatettu arvo:
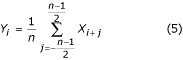
on vaiheeltaan yhteneväinen suodattamattoman arvon kanssa.
Jos kyseessä on parillinen luku n = 2m, nämä kaksi arvoa ovat puoli näytteenottojakson verran vaihesuuntautuneita:
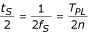
mutta muuttuvat vaiheyhteensopiviksi kaavalla
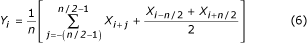
Keskiarvoistukseen voidaan ottaa joka toinen, kolmas tai q:s näyte, jos n/q on kokonaisluku. Riippuen siitä, onko n/q pariton vai parillinen, käytetään vastaavasti yhtälöä (7) tai (8).

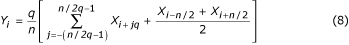
Erikoistapaus maksimaalisesta otoksen pienentämisestä syntyy, kun q = n/2 . Vastaava kaava:
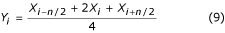
on nimeltään ’kolmen pisteen’ suodatin. Yhtälön (8) lisäksi voidaan soveltaa myös seuraavaa kaavaa
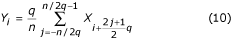
, jos q on parillinen. Jos q = n/2, suodattimesta tulee ”kaksipistesuodatin” ja se esitetään kaavalla:

Vähennetty näytteiden lukumäärä interferenssijaksossa johtaa kampasuodattimen lohkojen jyrkempään kaltevuuteen ja lyhentää laskenta-aikaa. Näitä ”etuja” on kuitenkin arvioitava huolellisesti, jotta Nyquistin sääntöä ei rikota, kun läsnä on suuri määrä kolmatta harmonista. Muita harmonisia ei oteta huomioon, koska korkeimmat parittomat harmoniset vaimennetaan yleensä alipäästösuodattimilla, joiden katkaisu on 100-150 Hz:n alueella, kun taas parilliset harmoniset puuttuvat käytännössä kokonaan sähkövoimaloiden generaattoreiden tarkan napavalmistuksen vuoksi.
PL-taajuuden vaihtelun kompensointi
Sallittua poikkeamaa PL-taajuuden nimellisestä taajuudesta rajoitetaan standardeissa joissakin maissa jopa 1 prosenttiin asti. Käytännössä poikkeama on usein suurempi. Kumaravel et al. raportoivat 3 prosentin vaihtelusta. McManus et al. havaitsivat huomattavia muutoksia häiriötaajuudessa, joka on päällekkäin Common Standards for Electrocardiography (CSE) -tietokannasta otetuissa tallenteissa.
Taajuusvaihtelut johtavat erikoistapaukseen, jossa näytteenotto ei ole moninkertainen ja jossa n on reaalinen kokonaisluvun n sijaan. Tämä komplikaatio voidaan kiertää, jos poikkeamat havaitaan jatkuvalla f PL:n laitteistomittauksella ja korjataan pienillä näytteenottovälin t S pienillä muutoksilla sen nimellisarvon (R) ympärillä, t RS = T RPL /n (tässä T RPL = 20 ms on nimellinen T PL, kun f RPL = 50 Hz). Kun f PL:n poikkeama on 49,5-50,1 Hz, t S:n vaihtelut ovat 1 %:n luokkaa, eivätkä ne näin ollen aiheuta virheitä, jotka ylittävät sellaisten parametrien hyväksytyn mittaustarkkuuden, joita yleensä käytetään automaattiseen EKG-luokitukseen.
Ensimmäinen lähestymistapa liittää jokaisen ensimmäisen näytteen, S 1 , laukaisemisen jaksoissa S k (k = 1, 2…n) jaksoissa T PL mielivaltaisesti valittuun, mutta pysyvään amplitudiin PL-jännitteestä. Seuraavien näytteiden, S k (k = 2…n), väli on t S , joka saadaan kaavalla t S = T RTL /n. Jos taajuus on 50 Hz ja n = 5, t S = 4 ms. Dotsinsky ja Daskalov tutkivat kahta erilaista virhetyyppiä, joihin tätä lähestymistapaa käyttäen on syyllistytty. Ensimmäinen virhe, joka johtuu näytteiden välisistä epäsäännöllisyyksistä, voi nousta 1 %:iin, kun f S = 400 Hz, ja 1,2 %:iin, kun f S = 250 Hz, jos poikkeama on 1 % f RPL:n ympärillä. Toinen virhetyyppi ei ylitä 3 %:a, ja se on seurausta suodatetun näytteen lisäksi siirtyneestä sijainnista.
Dotsinsky ja Daskalov raportoivat parannetun lähestymistavan. Jatkuva jakso T PL mitataan ja jaetaan n:llä. Saatua t S:ää käytetään seuraavassa T PL:ssä.
Menettelyn tehokkuuden arviointi
Subtraktiomenettelyn esimerkit on esitetty kuvissa 4 ja 5. EKG-signaalit on otettu American Heart Associationin tietokannasta. Signaalit on lovisuodatettu 60 Hz:n (PL-taajuus Yhdysvalloissa) häiriöiden poistamiseksi. Sitten signaalit sekoitetaan 50 Hz:n häiriöihin, joiden amplitudi on moduloitu 0-3,2 mVp-p 200 μVs-1:n nousunopeudella. Jäljet tunnistetaan seuraavasti: i) tulosignaali; ii) syntetisoitu häiriö; iii) sekoitettu signaali; iv) käsitelty signaali; v) alkuperäisen ja käsitellyn signaalin välinen ero ja vi) suurennettu ero. Hylätyt komponentit sisältävät itse asiassa myös elektromyografisia (EMG) ja muita häiriöitä. Eroissa on myös signaalin vaimentamaton osa yhdessä pienten jäännöshäiriöiden ja M-arvon kanssa tehdyistä kompromisseista johtuvien vääristymien kanssa.
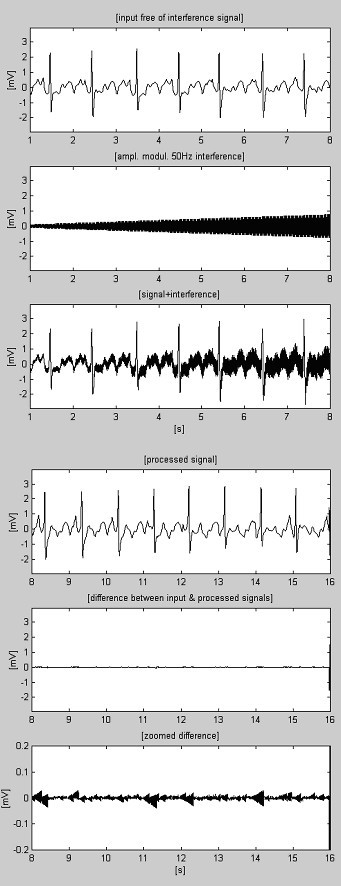
Käsitelty AHA 3004d1 -tallennus.
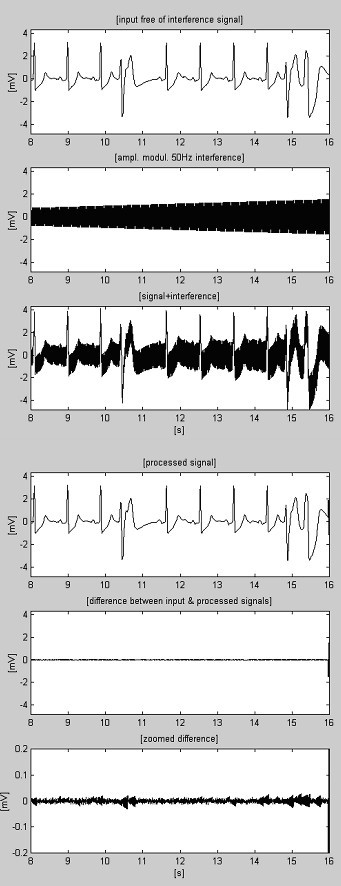
Käsitelty AHA 6007d1 -tallennus.
Kahden signaalin avulla arvioidaan subtraktiomenettelyn tehokkuutta vain häiriöiden osalta. Ensimmäistä, omasta tietokannastamme otettua signaalia kutsutaan ehdollisesti ”puhtaaksi” (kuva 6). Tulos osoittaa pieniä eroja syötetyn ja käsitellyn signaalin välillä, mikä johtuu silmämääräisesti syötetyssä signaalissa esiintyvästä kohinasta. Tämä tulos tarkistetaan toisella syntetisoidulla signaalilla, joka ei sisällä häiriöitä (kuva 7). Kuten voidaan nähdä, vääristymiä ei esiinny. Sama syntetisoitu signaali asetetaan päällekkäin häiriöiden kanssa ja käsitellään (kuva 8). Jäännöshäiriöitä ei ole havaittavissa.
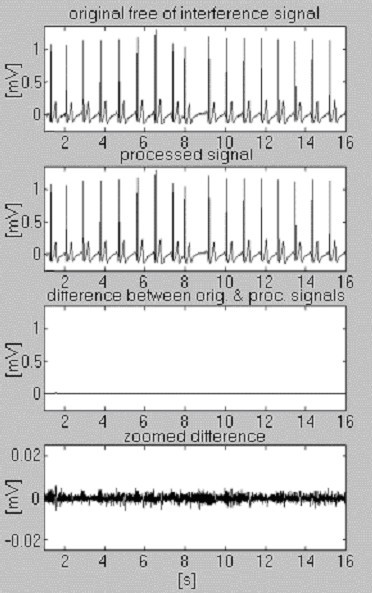
Edellytyksellisesti ”puhtaan” signaalin käsittely.
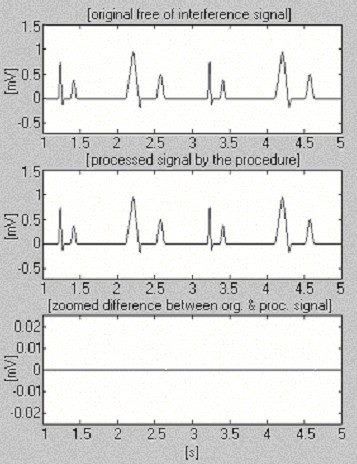
Syntetisoidun signaalin käsittely.
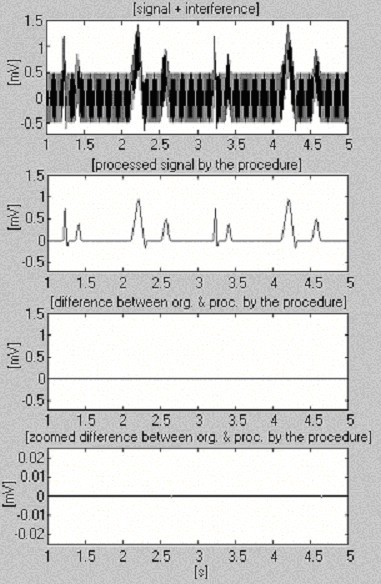
Syntetisoidun signaalin+häiriöiden käsittely.
EMG-kohinan vaikutus
Joskus EMG-kohina on niin suurta, että lineaarisen segmentin löytäminen vaikeutuu. Tämän seurauksena epätarkat korjaukset, jotka eivät vastaa häiriöamplitudin viimeistä muutosta, aiheuttavat virheitä (ks. jäännöskohina 11. ja 14. s:n välillä kuvassa 9).
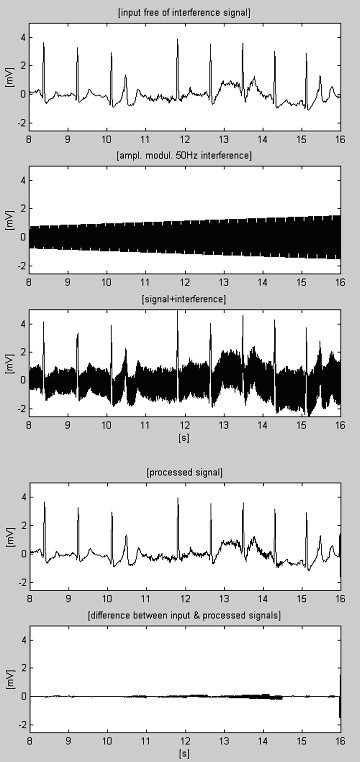
Käsitelty EKG-signaali+EMG-kohina+häiriö.
Erittäin yksinkertainen lähestymistapa EMG-kohinan vaikutuksen tukahduttamiseksi menettelyyn ottaa käyttöön ylimääräisen rinnakkaisen puskurin, jossa meneillään olevat signaalin osat ehdoitta keskiarvoistetaan . Tätä puskuria käytetään tarkkaan lineaarisuuden havaitsemiseen. Kuvissa 10 ja 11 esitetään tulosten vertailu ilman rinnakkaispuskuria ja rinnakkaispuskurin kanssa. Jäljet ”a” edustavat EKG-signaalia, johon on sekoitettu häiriöitä ja EMG-kohinaa. Jäljet ”b” kuvassa 10 ja ”c” kuvassa 11 osoittavat siirtymiä lineaarisista segmenteistä epälineaarisiin segmentteihin (on-off-funktiot). Kuten voidaan nähdä, kuvan 10 keskiarvoistettu signaaliosa on hyvin rajallinen. Tämän seurauksena menettelyn tehokkuus heikkenee (kuvat 10c ja 10d. Sen sijaan rinnakkaispuskuri mahdollistaa pitkien lineaaristen segmenttien havaitsemisen (kuva 11c), ja jäännöskohina käsitellyssä signaalissa (kuva 11d) on vähäistä. Kohinaa ei kuitenkaan tukahduteta kokonaan, koska osa siitä osallistuu korjauslaskentaan.
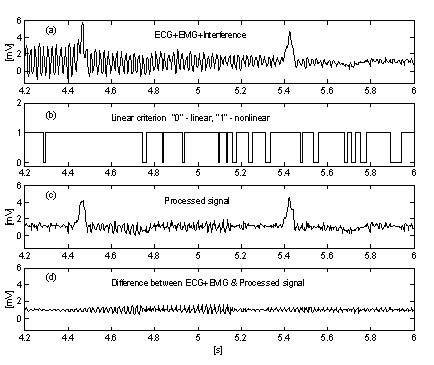
Häiriö+EMG-kohinan poisto ilman rinnakkaispuskuria.
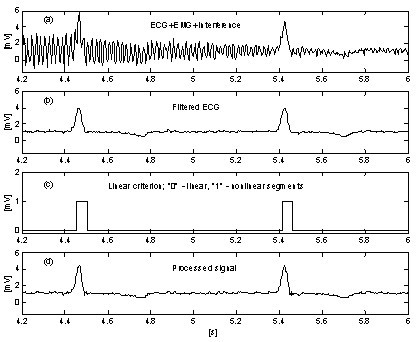
Interferenssi+EMG-kohinan subtraktio rinnakkaispuskurin kanssa.
Lisäparannusta EMG-kohinan vaimentamiseen Christov saa käyttämällä adaptiivista kynnysarvoa M, joka lasketaan suhteessa kohinan/signaalin suhdelukuun Rt, joka on määritelty seuraavasti: Rt = S NL /S F, jossa kohinataso S NL on yhtä suuri kuin epookin S F epookin epälineaaristen segmenttien yhteenlaskettu leveys, joka vastaa suurin piirtein tarkastelun kohteena olevaa RR-intervallia. Lineaarisuushaku kriteerillä M = 150 μV ”puhtaalle” EKG:lle (kuva 12a) ja samalle signaalille, mutta EMG-kohinan saastuttamana (kuva 12b), osoittaa erilaisia S NL -arvoja (kuvat 12c ja 12d). Menetelmä on kehitetty MATLAB-ympäristössä. Alustava kynnysarvo M on valittu 30 μV:ksi. Sen jälkeen sitä nostetaan asteittain, kunnes Rt saavuttaa 10 %, minkä jälkeen aloitetaan subtraktiomenettely. Tasoa Rt ≤ 0,1 ehdotetaan QRS-leveyden ja sen RR-välin suhteen perusteella, joka on yleensä noin 10 %. Sekä häiriöiden että EMG-kohinan poistaminen voidaan havaita kuvissa 13b ja 13d, joissa käytetään M = 420 μV. Vertailun vuoksi ”puhdasta” EKG-signaalia käsitellään M = 35 μV:llä (kuvat 13a ja 13c).

Kohinatasot SNL (jäljet c ja d) ”puhtaassa” EKG-signaalissa (jälki a) ja EMG:n saastuttamassa signaalissa (jälki b).
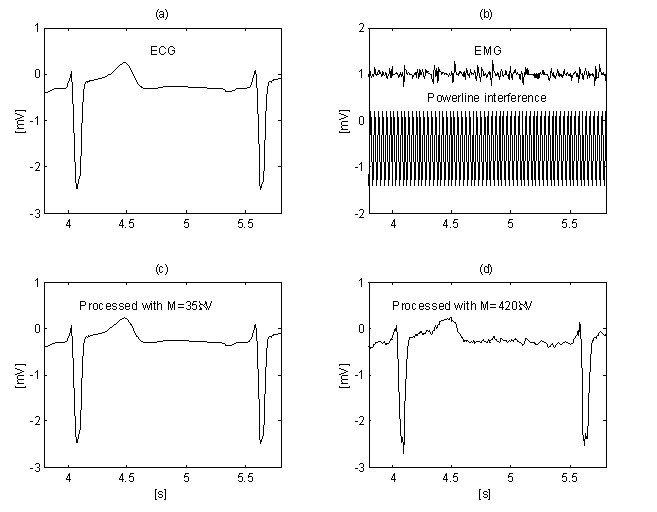
Häiriöiden + EMG-kohinan vaimentaminen adaptiivisella kynnysarvolla M: ’puhdas signaali’ (a), joka on käsitelty menetelmällä M = 35 μV (c), ja kontaminoitunut signaali (b), johon on sovellettu menettelyä menetelmällä M = 420 μV (d).
Lineaarisia segmenttejä ei löydy säännöllisesti eteis- ja kammiovärinäpotilailta. Aaltomuodon täydellinen säilyttäminen ei kuitenkaan ole välttämätöntä värinän havaitsemiseksi, joten kaikenlaisia perinteisiä suodattimia voidaan käyttää.
Häiriöiden vaimentaminen korkean resoluution EKG:ssä
Subtraktiomenetelmä ei ole suoraan sovellettavissa kehon pinnalla olevaan His-EKG:hen, koska matalaamplitudista ja suhteellisen matalataajuista His-aaltoa ei voida erottaa lineaarisissa segmenteissä. Näin ollen His-aalto käytännössä tukahdutetaan tai jopa poistetaan signaalista. EMG-kohina on yleensä amplitudiltaan ja taajuussisällöltään paljon suurempaa kuin pinnan His-aalto. Siksi pelkkä kynnysarvon M muuttaminen ei johda lineaaristen ja epälineaaristen segmenttien hyväksyttävään erotteluun.
Bazhina ym. toteuttivat seuraavan muutoksen. Havaitun epälineaarisen segmentin alkua ennen QRS-kompleksia siirretään 100 ms vasemmalle, jolloin His-aallon alue määritellään oletusarvoisesti epälineaariseksi segmentiksi (kuva 14).
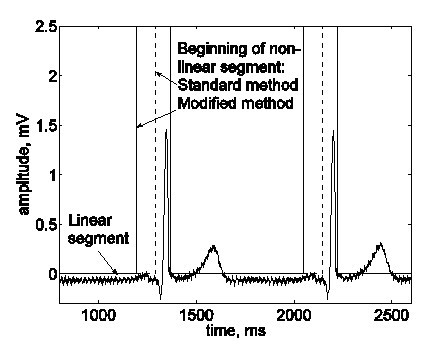
QRS-kompleksin sisältävän epälineaarisen segmentin alku siirrettiin oletusarvoisesti 100 ms vasemmalle, jotta se sisältäisi vyöhykkeen, jossa His-kimppuisen aallon odotetaan esiintyvän.
Subtraktiomenetelmää ja kolmea muuta menetelmää: lovisuodattimia, spektraalista interpolointia ja regressiosubtraktiota testattiin alkuperäisen signaalin minimaalista vääristymistä vastaan. Subtraktiomenetelmä ja regressiosubtraktiomenetelmä osoittautuivat parhaiksi, sillä Baratta et al. käyttävät vastaavaa konseptia lineaaristen segmenttien kohinan estimointiin. Regressio-subtraktio käsittelee huonosti häiriön amplitudimuutoksia nykyisen segmentin sisällä.
Paristokäyttöisten laitteiden ja tietokoneavusteisten EKG-järjestelmien tapaus
Häiriön taajuusmodulaation kompensoimiseksi tarvittava f PL:n laitteistomittaus ei ole toteutettavissa paristokäyttöisissä laitteissa ja joissakin tietokoneavusteisissa EKG-järjestelmissä. Dotsinsky ja Stoyanov tutkivat vakioamplitudin omaavien häiriöiden taajuusmuutosten vaihteluväliä, jolla jäännösosa rajoitetaan hyväksyttävälle tasolle ilman synkronoitua näytteenottoa. He havaitsivat, että alle 20 μVp-p:n jäännöshäiriö voidaan saada aikaan menettelyllä, jossa: i) häiriön amplitudi ≤ 0,4 mVp-p ja ii) taajuuden muutos nopeudella ≤ 0,0125 Hz-1. Koska tällaiset virtalähteelle asetetut vaatimukset voidaan usein ylittää, kehitettiin ohjelmistollinen häiriöiden mittaus.
EKG-signaali käsitellään aluksi 49-51 Hz:n kaistanpäästösuodattimella. Mitataan kahden vierekkäisen näytteen, Br L ja Br R , amplitudit, jotka on otettu nollaviivan alapuolella ja yläpuolella olevasta interferenssin positiivisesta kaltevuudesta (kuva 15). Interferenssin nollapisteen CP ja oikean näytteen, Br R , välinen etäisyys, t CP , lasketaan jatkuvasti seuraavasti:
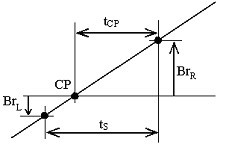
Interferenssin nollapisteen ylitys.

T PL:n muuttuessa t S määritellään uudelleen käyttäen

Tämä lähestymistapa toteutettiin MATLAB-ympäristössä. Kun näytteenottotaajuus f S = 500 Hz ja f RPL = 50 Hz, n on 10. Tuote kn määrittää ajan, jonka suositellaan kuluvan ennen uuden tCP,i + kn laskemista ja edellisen tCP,i:n korvaamista uudella tCP,i:llä. Kuvassa 16 esitetään käsitelty 1 mV:n EKG-signaali sen jälkeen, kun se on sekoitettu interferenssillä, jonka amplitudi on vakio 2 mVp-p ja jonka taajuus vaihtelee erittäin nopeasti 1 Hz:n taajuudella 8 s:n välein (ensimmäinen jälki). Saadun tehokkuuden arvioimiseksi esitetään myös suurennettu erotus ilman synkronoitua näytteenottoa (viimeinen jälki).
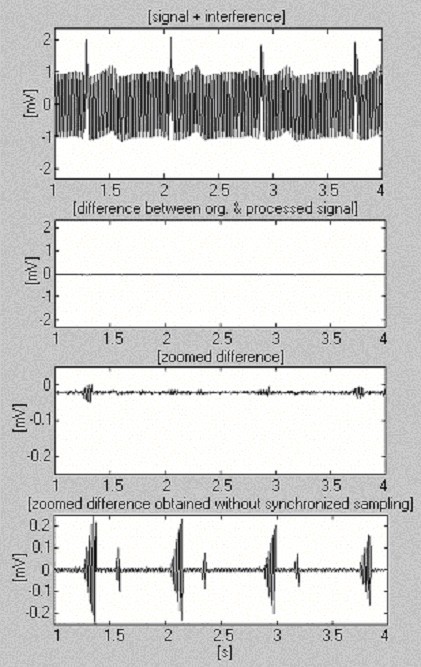
Subtraktiomenetelmä, jossa käytetään ohjelmiston voimajohtotaajuuden mittausta.
Seuraavana loogisena askeleena on: i) säilytetään EKG-laitteen nimellinen t S, ii) näytteistetään signaali uudelleen meneillään olevan mitatun f PL:n mukaisesti häiriöiden poistamiseksi ja iii) palataan nimelliseen t S:ään. Tällaisen lähestymistavan ensimmäiset tulokset ovat erittäin lupaavia. Näin ollen muuttujan f PL ohjelmistokompensointi sekä subtraktiomenettelyn kokonaistoteutus instrumentissa, mukaan lukien automaattinen säätö 50 tai 60 Hz:n f RPL:lle, saadaan valmiiksi laitteistopiireistä ja vastaavasta ohjelmistosta riippumatta.
Automaattinen sovitus nimelliselle PL-taajuudelle
Vaihtoehtoisen häiriöiden vähennysmenetelmän yhteinen ohjelma 50 ja 60 Hz:n ympäristössä johtaa ei-moninkertaiseen näytteenottoon eli reaaliseen n:ään. Laajasti käytetyt t S:n arvot f RPL = 50 Hz:n tapauksessa, kuten 250, 500 ja 1000 Hz, vastaavat epärationaalista n:ää, joka on suuruusluokkaa 4.1(6), 8.3(3) ja 4.1(6), jos 60 Hz:n taajuudella esiintyviä häiriöitä halutaan poistettavan. Käänteisessä tapauksessa f S = 360 Hz edellyttää n = 7,2. Pyöristettyjä arvoja n* ei voida käyttää, koska ne aiheuttaisivat huomattavaa virhettä.
Dotsinsky ja Stoyanov löysivät hyvin yksinkertaisen ratkaisun, joka ei tarvitse f S:n muutosta. Alkuperäisessä menettelyssä käytetään kampasuodatinta interferenssin yhden jakson, T PL , aikana. Näin ohjelma toimii nopeammin. Yleensä n voidaan ottaa k > 1 kokonaisesta jaksosta. Menettely toimii, jos:
n = kT PL /t S on kokonaisluku.
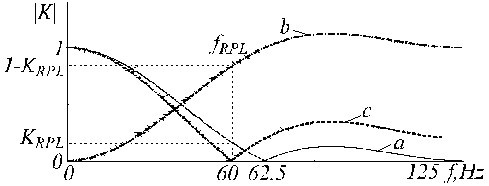
Jos t S = 2 ms (f S = 500 Hz) ja f RPL = 50 Hz, pienin k:n arvo, joka tyydyttää yhtälön (14), on oikeastaan k = 1. 60 Hz:n tapauksessa k on kuitenkin 3. Myös 20 ja 40 Hz:n alaharmonioihin liittyviä nollia esiintyy, mutta niillä ei ole vaikutusta menettelyyn. Näin ollen riittää, että n vaihdetaan 10:n (k = 1) ja 25:n (k = 3) välillä, jotta voidaan toimia molempien häiriöiden kanssa. Tätä tarkoitusta varten kaksi digitaalista kaistanpäästösuodatinta tarkastaa saapuvan signaalin. Kuvasta 17 nähdään, että suodatin, jonka taajuuskaista on päällekkäinen häiriön kanssa, tuottaa kertaluokkaa suuremman lähtösignaalin kuin toinen suodatin.
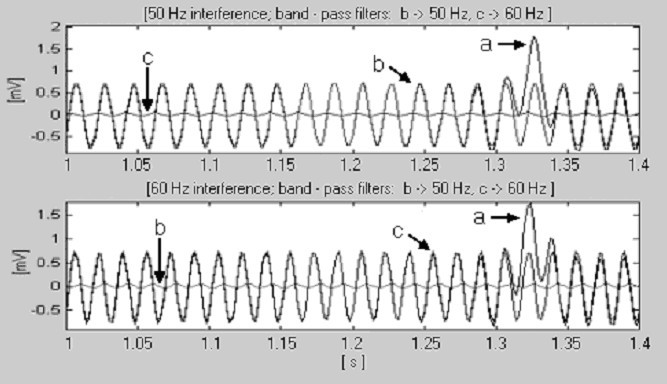
Nimellisen verkkotaajuuden havaitseminen, a) osa QRS-kompleksista, b) 50 Hz:n taajuuden häiriö ja c) 60 Hz:n taajuuden häiriö.
Teoreettisen menettelyn kehittäminen
Subtraktiomenettelyn teoriaa kehittivät edelleen Mihov , Levkov ja Mihov sekä Mihov ym. He ehdottivat neljää erilaista suodatintyyppiä, jotka on toteutettu yleistetyllä rakenteella, jolla voidaan ratkaista ongelmat lähes kaikissa tapauksissa, joissa ei ole moninkertaista näytteenottoa, mukaan lukien häiriöiden taajuusvaihtelut, ilman synkronoitua AD-muunnosta.
Ns. D-suodatin moninkertaisessa näytteenotossa määritellään on Cr yhtälössä (2), jossa toinen ero, D i , saadaan FD s:llä, jotka ovat yhden T PL:n välein:
D i = (X i+n – X i ) – (X i – X i-n ) = X i-n – 2X i + X i+n (15)
D-suodattimen siirtofunktiolla on nollakohdat pisteissä f = 0 ja f = f PL Hz, joka on kuvassa esitetty yhtä suurena kuin 50 Hz. 18.

D-suodattimen siirtofunktio fPL = 50 Hz:lle.
K-suodatin kuvaa yhtälöiden (5) ja (6) esittämää liukuvaa keskiarvoa. Sen siirtofunktio on esitetty kuvassa 19 n = 5:lle parittoman kertaluvun tapauksessa.
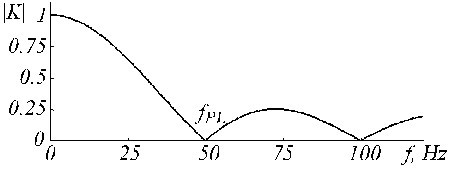
K-suodattimen siirtofunktio, kun fPL = 50 Hz ja n = 5.
Häiriökomponenttien jatkuvaan laskentaan käytetty yhtälö:
B i = X i – Y i (16)
määrittelee itse asiassa digitaalisen suodattimen nimeltä (1-K)-suodatin.
Suodattimet määritellään lisäksi uudelleen, kun näytteenotto ei ole moninkertainen, ja f S = 250 Hz yhdessä f RPL = 60 Hz:n kanssa otetaan huomioon ohjelmiston parannuksen havainnollistamiseksi.
Transferfunktion nollakohtien säilyttämiseksi D-suodatin on vähennettävä korjaussuodattimella, jonka nollakohta on nollakohta f = 0 ja jonka vahvistusarvot ovat D RPL:n kohdalla f = f RPL , joka on yhtä suuri kuin saman taajuuden D-suodattimen vahvistusarvot samalla taajuudella f RPL . Korjaussuodattimen synteesi perustuu kolmipisteiseen apusuodattimeen, joka annetaan yhtälöllä:

jossa (n/2)* on n/2:n pyöristetty arvo.
Sen vuoksi, että A RPL on apusuodattimen vahvistus taajuudella f = f RPL , korjaussuodatin kerrotaan suhdeluvulla D RPL /A RPL . Vastaavien siirtofunktioiden avulla D RPL ja A RPL lasketaan etukäteen seuraavasti:
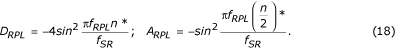
Viimein korjattu D*-suodatin esitetään

ja se on esitetty kuvassa 20 jäljellä ’c’, jossa jäljet ’a’ ja ’b’ kuvaavat D- ja korjaussuodatinta.
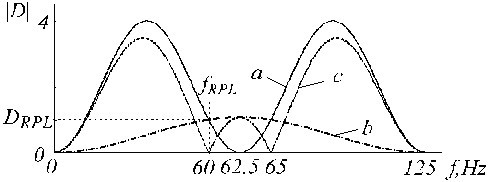
A) D-suodattimen, b) ylimääräisen korjaussuodattimen ja c) korjatun D-suodattimen siirtofunktiot.
K-suodattimen siirtofunktion on säilyttävä nollana, kun f = f RPL , ykkösvahvistus, kun f = 0 ja lineaarinen vaihevaste. K-suodattimen korjausmenettely on samanlainen kuin edellinen. Apusuodatin saadaan korjausten laskennassa käytetyllä kaavalla:
A i = X i – Y i , (20)
Suodattimen vahvistus on yhtä suuri kuin 1 – K RPL, kun f = f RPL , missä K RPL on K-suodattimen vahvistus samalle taajuudelle f RPL . Apusuodatin kerrotaan K RPL /(1 – K RPL ) ja vähennetään K-suodattimesta. Korjatun K*-suodattimen yhtälö on:
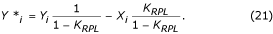
Vakio K RPL voidaan arvioida:

parittomalle tai parilliselle kertaluvulle vastaavasti.
Esimerkki K-suodattimen korjauksesta on esitetty kuvassa 21, jossa jäljet ”a”, ”b” ja ”c” kuvaavat ensisijaista K-suodatinta, apusuodatinta ja korjattua K*-suodatinta.
A) K-suodattimen, b) apukorjaussuodattimen ja c) korjatun K-suodattimen siirtofunktio.
Ei-monikerrosnäytteenotossa syntyy vaihe-ero meneillään olevien EKG-näytteiden ja häiriökomponenttien B i (yhtälö 16) välille, jotka sijaitsevat yleensä väliaikaisessa FIFO-puskurissa (FIFO-puskuri, first-in-first-out). Siksi B i:tä on muutettava vähentämällä se EKG-näytteistä epälineaaristen segmenttien aikana. Kompensointimenettely on suhteellisen monimutkainen. Kuvassa 22 esitetään väliaikaisen puskurin sisältö. Nykyinen häiriönäyte B i-n * ei ole sama kuin palautettu näyte B i . Sen amplitudi on laskettava uudelleen niiden välisen vaihe-eron kompensoimiseksi. Tämä toteutetaan uudella suodattimella, jonka vaihevaste on lineaarinen ja vahvistus on yksikäsitteinen, kun f = f RPL, ja jota kutsutaan B-suodattimeksi. Se syntetisoidaan tunnetusta K-suodattimesta, jonka ikkuna on sama kuin häiriöjakso. Jos n* on pariton, se voidaan kuvata seuraavasti:
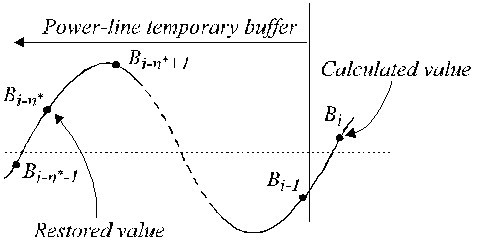
Väliaikaisen puskurin palautetut arvot.
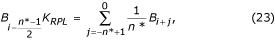
joissa K RPL on yhtälön (22) antama keskiarvosuodattimen häiriövahvistus.
Palautettu puskuriarvo B i voidaan laskea seuraavasti:
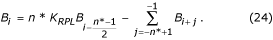
Tapauksessa, jossa n* on parillinen:
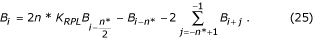
B-suodattimen siirtofunktio on esitetty kuvassa. 24, jossa subtraktiomenettelyn moduulit ovat seuraavat:
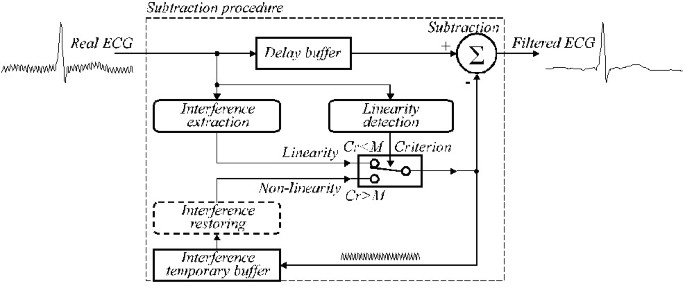
Subtraktiomenettelyn yleistetty rakenne.
-
Lineaarisuuden tunnistus. D-suodatinta käytetään kunkin signaalinäytteen naapuruston lineaarisuuden arviointiin.
-
Häiriöiden poisto. (1-K)-suodatinta käytetään häiriökomponentin laskemiseen.
-
Kriteeri. Ehto Cr <M lähettää joko uutetun tai palautetun PL-interferenssin Subtractioniin.
-
Interferenssin väliaikainen puskuri. Poistettu tai palautettu häiriökomponentti, jota käytetään korjauksena epälineaarisessa segmentissä, tallennetaan sijaintiin, joka on lukittu voimajohtohäiriön meneillään olevan vaiheen kanssa.
-
Häiriön palautus. B-suodatinta kutsutaan, jos näytteenotto ei ole moninkertainen, jotta voidaan palauttaa todelliset korjausarvot, jotka on vähennettävä tulosignaalin näytteistä epälineaarisissa segmenteissä.
-
Viivepuskuri. Kompensoi viivettä, joka ilmenee D-suodattimen ja (1-K)-suodattimen yhteydessä ja joka on välttämätön, jos menettely suoritetaan lähes reaaliajassa. Muussa tapauksessa puskuri voidaan jättää huomiotta.
-
Subtraktio. Poistettu tai palautettu häiriöarvo vähennetään viivästyneestä tulosignaalista ”puhtaan” EKG-signaalin tuottamiseksi. Epälineaarisuuden tapauksessa sekä interferenssin poisto että subtraktio toteuttavat K-suodattimen.
Yleistetyn rakenteen mukaista parannettua algoritmia on testattu off-line. Tulokset f S = 250 Hz:lle ja f RPL = 60 Hz:lle on esitetty kuvassa 25.
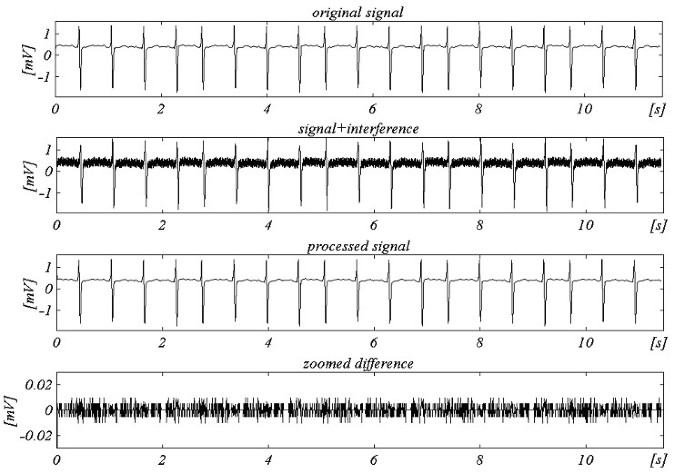
Esimerkki ei-monikerrosnäytteenotosta fRPL = 60 Hz:n ja fS = 250 Hz:n taajuudella.