Den tredje lagen postulerar att entropin i ett ämne alltid är ändlig och att den närmar sig en konstant när temperaturen närmar sig noll. Värdet på denna konstant är oberoende av värdena på alla andra tillståndsfunktioner som karakteriserar ämnet. För varje givet ämne är vi fria att tilldela ett godtyckligt valt värde till gränsvärdet vid nolltemperaturen. Vi kan dock inte tilldela alla ämnen godtyckliga nolltemperaturentropier. Den uppsättning tilldelningar vi gör måste stämma överens med de experimentellt observerade nolltemperatursgränsvärdena för entropiförändringarna vid reaktioner mellan olika ämnen. För perfekt kristallina ämnen är alla dessa reaktionsentropier noll. Vi kan uppfylla detta villkor genom att tilldela ett godtyckligt värde till varje grundämnes molära entropi vid nolltemperatur och fastställa att nolltemperaturentropin hos en förening är summan av nolltemperaturentropin hos de ingående grundämnena. Denna beräkning förenklas avsevärt om vi låter nolltemperatursentropin för varje grundämne vara noll. Detta är det väsentliga innehållet i den tredje lagen.
Lewis och Randalls uttalande innehåller detta val av nollentropi-referenstillstånd för entropier genom att ange det som ”ett kristallint tillstånd” för varje grundämne vid noll grader. Som ett resultat av detta är entropin för varje ämne vid noll grader större än eller lika med noll. Det innebär att Lewis och Randalls uttalande innehåller en konvention som fastställer gränsvärdet vid nolltemperatur för entropin hos alla ämnen. I detta avseende gör Lewis och Randalls uttalande ett i huvudsak godtyckligt val som inte är en inneboende egenskap hos naturen. Vi ser dock att det är ett överväldigande bekvämt val.
Vi har diskuterat alternativa uttalanden av den första och andra lagen. Ett antal alternativa uttalanden av den tredje lagen är också möjliga. Vi överväger följande:
Det är omöjligt att uppnå en temperatur på absolut noll.
Detta påstående är mer allmänt än Lewis och Randalls påstående. Om vi betraktar tillämpningen av detta påstående på de temperaturer som kan uppnås i processer som involverar ett enda ämne, kan vi visa att det implicerar, och är implicerat av, Lewis och Randalls påstående.
Värmekapacitetens egenskaper, \(C_P\), spelar en central roll i dessa argument. Vi har sett att \(C_P\) är en funktion av temperaturen. Även om det inte är användbart att göra det, kan vi tillämpa det definierande förhållandet för \(C_P\) på ett ämne som genomgår en fasövergång och finna \(C_P=\infty\). Om vi tänker på ett ämne vars värmekapacitet är mindre än noll stöter vi på en motsägelse av våra grundläggande idéer om värme och temperatur: Om \(q>0\) och \({q}/{\Delta T}<0\) måste vi ha \(\Delta T<0\); det vill säga, uppvärmning av ämnet får dess temperatur att sjunka. Kort sagt, den teori vi har utvecklat inrymmer premisser som kräver \(C_P>0\) för varje system som vi kan göra mätningar på.
Låt oss karakterisera ett system med ren substans genom dess tryck och temperatur och betrakta reversibla processer med konstant tryck i vilka endast tryck-volymarbete är möjligt. Då är \({\left({\partial S}/{\partial T}\right)}_P={C_P}/{T}\) och \(dS={C_PdT}/{T}\). Vi vill nu visa: Lewis och Randalls villkor att entropin alltid är ändlig kräver att värmekapaciteten går till noll när temperaturen går till noll. (Eftersom vi ska visa att den tredje lagen förbjuder mätningar vid den absoluta nollpunkten är denna slutsats förenlig med vår slutsats i föregående stycke). Att värmekapaciteten går till noll när temperaturen går till noll framgår av \(S={C_PdT}/{T}.\) Om \(C_P\) inte går till noll när temperaturen går till noll, blir \(dS\) godtyckligt stor när temperaturen går till noll, vilket motsäger Lewis och Randalls påstående.
För att utveckla detta resultat mer explicit låter vi värmekapaciteten vid temperatur \(T\) och noll vara \(C_P\left(T\right)\) respektive \(C_P\left(0\right)\). Eftersom \(C_P\left(T\right)>0\) för varje \(T\ >0\), har vi \(S\left(T\right)-S\left(T^*\right)>0\) för varje \(T>T^*>0\). Eftersom entropin alltid är ändlig, \(\infty >S\left(T\right)-S\left(T^*\right)>0\), så att
\\\ }>0\]
och
\
för temperaturer i närheten av noll, kan vi expandera värmekapaciteten, med godtycklig noggrannhet, som en Taylor-serie polynom i \(T\):
\
Ojämlikheterna blir
\
Det vänstra villkoret kräver \(C_P\left(0\right)=0\).
Vi kan se den tredje lagen som ett uttalande om värmekapaciteten hos rena ämnen. Vi drar inte bara slutsatsen att \(C_P>0\) för alla \(T>0\), utan också att
\
Mer generellt kan vi dra slutsatsen att motsvarande påståenden gäller för slutna reversibla system som inte är rena ämnen: \({{\left({\partial H}/{\partial T}\right)}_P>0\) för alla \(T>0\), och \({\mathop{\mathrm{lim}}_{T\to 0} T^{-1}{\left({\partial H}/{\partial T}\right)}_P=0\ }\). (Nolltemperaturentropierna för sådana system är dock inte noll.) I diskussionen nedan beskriver vi systemet som en ren substans. Vi kan föra i stort sett samma resonemang för vilket system som helst; vi behöver bara ersätta \(C_P\) med \({\left({\partial H}/{\partial T}\right)}_P\). Lewis och Randalls påstående hävdar att entropin blir konstant vid den absoluta nollpunkten, oberoende av värdena för alla andra termodynamiska funktioner. Därav följer att entropin vid noll grader är oberoende av tryckets värde. För två tryck, \(P_1\) och \(P_2\), gäller \(S\vänster(P_2,0\right)-S\vänster(P_1,0\right)=0\). Om vi låter \({P=P}_1\) och \(P_2=P+\Delta P\) och , har vi
\
för varje \(\Delta P\). Därför har vi
\
I kapitel 10 finner vi \({\left({\partial S}/{\partial }P\right)}_T=-{\left({\partial V}/{\partial T}\right)}_P\), så både entropin och volymen närmar sig sina nolltemperatursvärden asymptotiskt.
När vi säger att den absoluta nollpunkten är ouppnåelig menar vi att inget system kan genomgå någon förändring där dess sluttemperatur är noll. För att se varför den absoluta nollpunkten måste vara ouppnåelig, låt oss betrakta processer som kan sänka temperaturen i ett system. I allmänhet har vi värmereservoarer som är tillgängliga vid olika temperaturer. Vi kan välja den tillgängliga reservoaren vars temperatur är lägst och föra systemet till denna temperatur genom enkel termisk kontakt. Så mycket är trivialt; utmaningen är uppenbarligen att sänka temperaturen ytterligare. För att göra det måste vi åstadkomma någon annan förändring. Vad denna förändring än må vara kan den inte främjas av ett värmeutbyte med omgivningen. När vi väl har fört systemet till temperaturen i den kallaste tillgängliga delen av omgivningen kan varje ytterligare utbyte av värme med omgivningen bara vara kontraproduktivt. Vi drar slutsatsen att varje process som lämpar sig för vårt syfte måste vara adiabatisk. Eftersom en adiabatisk process inte utbyter någon värme med omgivningen, \(\Delta \hat{S}=0\).
Processen måste också vara en möjlig process, så att \(\(\Delta S+\Delta \hat{S}\ge 0\), och eftersom den är adiabatisk, \(\(\Delta S\ge 0\). Låt oss betrakta en reversibel process och en irreversibel process där samma system\({}^{2}\) går från det tillstånd som anges av \(P_1\) och \(T_1\) till ett andra tillstånd där trycket är \(P_2\). Sluttemperaturerna och entropiförändringarna för dessa processer är olika. För den reversibla processen är \(\(\Delta S=0\); vi anger sluttemperaturen som \(T_2\). För den irreversibla processen, \(\Delta S>0\); vi anger sluttemperaturen som \(T^*_2\). Det visar sig att temperaturförändringen är mindre för den irreversibla processen än för den reversibla processen, dvs. \(T_2-T_1<t^*_2-t_1\)>. På motsvarande sätt når den reversibla processen en lägre temperatur: \({T_2<t}^*_2\)>. Från
\
kan vi beräkna entropiförändringarna för dessa processer. För den reversibla processen beräknar vi \
För att göra detta beräknar vi först
\
för den isotermiska reversibla omvandlingen från tillståndet \(P_1\), \(T_1\) till det tillstånd som specificeras av \(P_2\) och \(T_1\). För detta steg är \(dT\) noll, och därför
\
Vi beräknar sedan
\
för den isobära reversibla omvandlingen från tillståndet \(P_2\), \(T_1\) till tillståndet \(P_2\), \(T_2\). För denna omvandling är \(dP\) noll, och
\
Då,
\
Då,
eftersom \(\(\(\Delta S^{rev}=0=0\), är den reversibla processen unik; det vill säga, givet \(P_1\), \(T_1\), och \(P_2\), bestäms systemets sluttemperatur. Vi finner \(T_2\) från
\
För att förstå entropiförändringen för den irreversibla processen noterar vi först att det finns ett oändligt antal sådana processer. Det finns inget unikt med sluttemperaturen. Givet \(P_1\), \(T_1\) och \(P_2\) kan sluttemperaturen \(T^*_2\) ha vilket värde som helst som är förenligt med ämnets egenskaper. För att specificera en viss irreversibel process måste vi specificera alla fyra storheterna \(P_1\), \(T_1\), \(P_2\) och \(T^*_2\). Efter att ha gjort detta kan vi emellertid beräkna entropiförändringen för den irreversibla processen,
\
genom att beräkna entropiförändringarna när vi på ett reversibelt sätt för systemet längs den isoterma tvåstegsvägen från \(P_1\), \(T_1\) till \(P_2\), \(T_1\) och sedan längs den isobariska vägen från \(P_2\), \(T_1\) till \(P_2\), \(T^*_2\). Beräkningen av \(\Delta S^{irrev}\) för denna reversibla väg från \(P_1\), \(T_1\) till \(P_2\), \(T^*_2\) använder samma logik som beräkningen, i föregående stycke, av \(\(\Delta S\) för den reversibla vägen från \(P_1\), \(T_1\) till \(P_2\), \(T_2\). Skillnaden är att \(T^*_2\) ersätter \(T_2\) som övre gräns i temperaturintegralen. Tryckintegralen är densamma. Vi har
\
Från \(\(\Delta S^{irrev}>\Delta S^{rev}\) har vi
\
Då integranterna är desamma och positiva, följer att \(T^*_2>T_2\), som hävdats ovan.
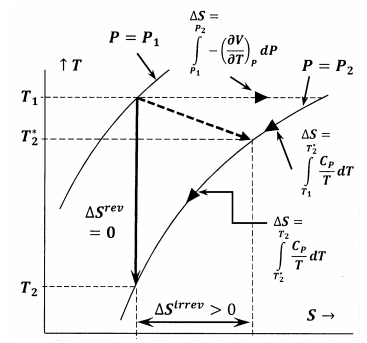
Figur 6 visar sambanden mellan de olika storheter som diskuteras i detta resonemang. I första hand visar figur 6 en plott av två av systemets isobarer i temperatur-entropirummet. Det vill säga, linjen \(P=P_1\) visar den uppsättning temperatur-entropipunkter där det jämviktade systemet har trycket \(P_1\); linjen \(P=P_2\) visar jämviktslägena vid trycket \(P_2\). Andra linjer i denna skiss representerar vägar längs vilka systemet kan genomgå reversibla förändringar vid konstant entropi eller konstant temperatur. Den streckade linjen representerar den irreversibla process där systemet går från tillståndet \(P_1\), \(T_1\) till tillståndet \(P_2\), \(T^*_2\). Denna linje är streckad för att representera det faktum att systemets temperatur kanske inte är väl definierad under den irreversibla processen.
Effektiv kylning kan uppnås med hjälp av tryckförändringar om systemet är en gas. För vätskor och fasta ämnen är dock \({\left({\partial V}/{\partial T}\right)}_P\) liten; följaktligen är temperaturförändringen för en reversibel tryckförändring också liten. Vid temperaturer nära den absoluta nollpunkten är nästan alla ämnen fasta. För att uppnå effektiv kylning måste vi ändra en termodynamisk variabel för vilken ett fast ämnes temperaturkoefficient är så stor som möjligt. För att kunna ta ställning till det allmänna problemet med att sänka temperaturen i ett system genom att variera något annat än trycket, måste vi betrakta ett system där någon form av icke tryck-volymarbete är möjligt. Ett sådant system är utsatt för en extra kraft, och dess energi förändras när denna kraft förändras.
Adiabatisk avmagnetisering
Den praktiska metod genom vilken extremt låga temperaturer uppnås kallas adiabatisk avmagnetisering. Denna metod utnyttjar egenskaperna hos paramagnetiska fasta ämnen. I sådana fasta ämnen ger oparade elektroner som är lokaliserade på enskilda atomer upphov till ett magnetiskt moment. Kvantmekaniken leder till viktiga slutsatser om interaktionen mellan sådana magnetiska moment och ett applicerat magnetfält: I ett tillämpat magnetfält är det magnetiska momentet hos en enskild atom kvantiserat. I det enklaste fallet kan det bara riktas i två riktningar; det måste vara antingen parallellt eller antiparallellt med det applicerade magnetfältet. När en atoms magnetiska moment är parallellt med magnetfältet är systemets energi mindre än när det är antiparallellt. Det applicerade magnetfältet utövar en kraft på de magnetiska moment som är associerade med enskilda atomer. Systemets energi beror på storleken av det applicerade magnetfältet.
Istället för att fokusera på det speciella fallet med adiabatisk avmagnetisering, låt oss betrakta de energi- och entropiförändringar som är förknippade med förändringar i en generaliserad potential, \({\mathit{\Phi}}_{\theta }\), och dess generaliserade förskjutning, \(\theta\). (För adiabatisk avmagnetisering är \(\theta\) det applicerade magnetfältet). Tre variabler krävs för att beskriva reversibla förändringar i detta system. Vi kan uttrycka energin och entropin som funktioner av temperatur, tryck och \(\theta\):
\(E=E\left(T,P,\theta \right)\) och \(S=S\left(T,P,\theta \right)\). Entropins totala differential inkluderar en term som specificerar entropins beroende av \(\theta\). Vi har
\
där vi skriver \(C\left(T,P,\theta \right)\) för att betona att våra nuvarande syften nu kräver att vi mäter värmekapaciteten vid konstant tryck och konstant \(\theta\).
För konstant tryck, P, och konstant förskjutning, \(\theta\), beror entropin på temperaturen som
\
Postulatet att entropin ska vara ändlig vid varje temperatur innebär att den tryck- och \(\theta\)-beroende värmekapaciteten blir noll vid absolut noll. Det vill säga, vid den absoluta nollpunkten försvinner värmekapaciteten oavsett värdena för P och \(\theta\). Argumentet är exakt detsamma som tidigare. Tidigare skrev vi \(C_P\left(0\right)=0\); för detta generaliserade fall skriver vi \(C\left(0,P,\theta \right)=0\).
Sålunda följer det av postulatet att entropin blir konstant vid absoluta nollpunkten för alla värden på de andra termodynamikvariablerna att för två valfria tryck \(P_1\) och \(P_2\), och för två valfria värden på den generaliserade förskjutningen, \({\theta }_1\) och \({\theta }_2\),
\
och därmed att
\ och \
Vi vill betrakta en process där ett system går från den lägsta temperatur som finns i omgivningen till en ännu lägre temperatur. För att minimera sluttemperaturen måste denna process genomföras adiabatiskt. Det måste också vara en möjlig process, så att \(dS\ge 0\). Låt oss nu för enkelhetens skull anta att vi utför denna process vid ett konstant tryck, \(P\), och att systemet går från tillståndet \(P\), \(T_1\), \({\theta }_1\), \({\theta }_1\) till tillståndet \(P\), \(T_2\), \({\theta }_2\) där \(T_1>T_2\). Entropierna för dessa två tillstånd är
\ och \
Entropen för denna process är
\ \
Entroppförändringen för denna process är
\ \
Vi kan nu anta att sluttemperaturen är noll; Det vill säga \(T_2=0\), så att
\ Det följer att \
där ojämlikheten till höger följer av det faktum att \(C\vänster(T,P,{\theta }_1\right)>0\). Av detta följer att
\
vilket motsäger Lewis och Randalls uttalande om den tredje lagen. Antagandet att systemet kan nå den absoluta nollpunkten leder till en motsägelse av Lewis och Randalls uttalande om den tredje lagen. Om Lewis och Randalls påstående är sant är därför den absoluta nollan ouppnåelig.
Det omvända gäller också; det vill säga, från satsen att den absoluta nollan är ouppnåelig kan vi visa att Lewis och Randalls påstående är sant. För att göra detta omformar vi ovanstående ekvation för \(\Delta S\),
\ \
Om vi nu antar att Lewis och Randalls påstående är falskt, kan uttrycket till höger vara mindre än eller lika med noll. Integralen till vänster kan då vara noll, i vilket fall systemet kan nå den absoluta nollpunkten. Om Lewis och Randalls påstående är falskt är det sant att systemet kan nå den absoluta nollpunkten. Därför: Om systemet inte kan nå den absoluta nollpunkten är Lewis och Randalls påstående sant.
Figurerna 7 och 8 visar dessa idéer med hjälp av konturplottar i temperatur-entropirum. Varje figur visar två konturlinjer. En av dessa konturlinjer är en uppsättning temperatur- och entropivärden längs vilka trycket är konstant vid \(P\) och \(\theta\) är konstant vid \({\theta }_1\). Den andra konturlinjen är en uppsättning temperatur- och entropivärden där trycket är konstant vid \(P\) och \(\theta\) är konstant vid \({\theta }_2\). Lutningen på en konturlinje är
\
Eftersom värmekapaciteten alltid är positiv är denna lutning alltid positiv.
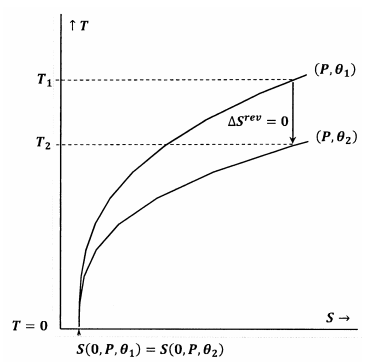
I figur 7 är Lewis och Randalls påstående uppfyllt. När temperaturen går till noll möts konturlinjerna vid samma entropivärde; dessa konturer uppfyller förhållandet
\
En adiabatisk (vertikal) väg från konturen för \(P\) och \({\theta }_1\) möter konturen för \(P\) och \({\theta }_2\) vid en positiv temperatur, \(T_2>0\). Eftersom detta uppenbarligen är sant för varje \(P\) och \({\theta }_2\), kommer sluttillståndet för varje adiabatisk process att ha \(T_2>0\). Eftersom Lewis och Randalls uttalande är uppfyllt kan systemet inte nå den absoluta nollpunkten, och vice versa.
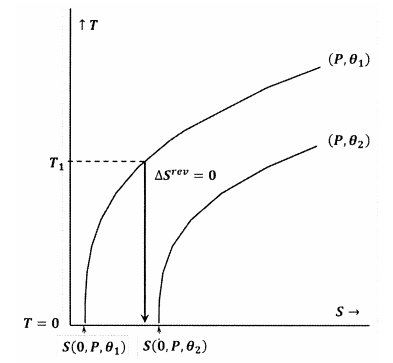
I figur 8 bryts Lewis och Randalls påstående eftersom vi har \(S\left(0,P,{\theta }_1\right)\). I detta fall kommer en adiabatisk process som inleds från en tillräckligt låg utgångstemperatur, \(T_1\), att nå den absoluta nollpunkten utan att skära konturen för konstanta \(P\) och \({\theta }_2\). Eftersom Lewis- och Randal-uttalandet bryts kan systemet nå den absoluta nollpunkten, och vice versa.