Vi började med 2D Convolutions i det första inlägget eftersom konvolutioner fick stor popularitet efter framgångar inom Computer Vision. Eftersom uppgifter inom detta område använder bilder som indata, och naturliga bilder vanligtvis har mönster längs två rumsliga dimensioner (höjd och bredd), är det vanligare att se exempel på 2D-konvolutioner än 1D- och 3D-konvolutioner.
Men på senare tid har man dock haft ett stort antal framgångar när det gäller att tillämpa konvolutioner även på uppgifter för behandling av naturliga språk. Eftersom uppgifter inom detta område använder text som indata, och text har mönster längs en enda rumslig dimension (dvs. tid), passar 1D-konvolutioner utmärkt! Vi kan använda dem som effektivare alternativ till traditionella recurrent neural networks (RNNs) såsom LSTMs och GRUs. Till skillnad från RNNs kan de köras parallellt för riktigt snabba beräkningar.
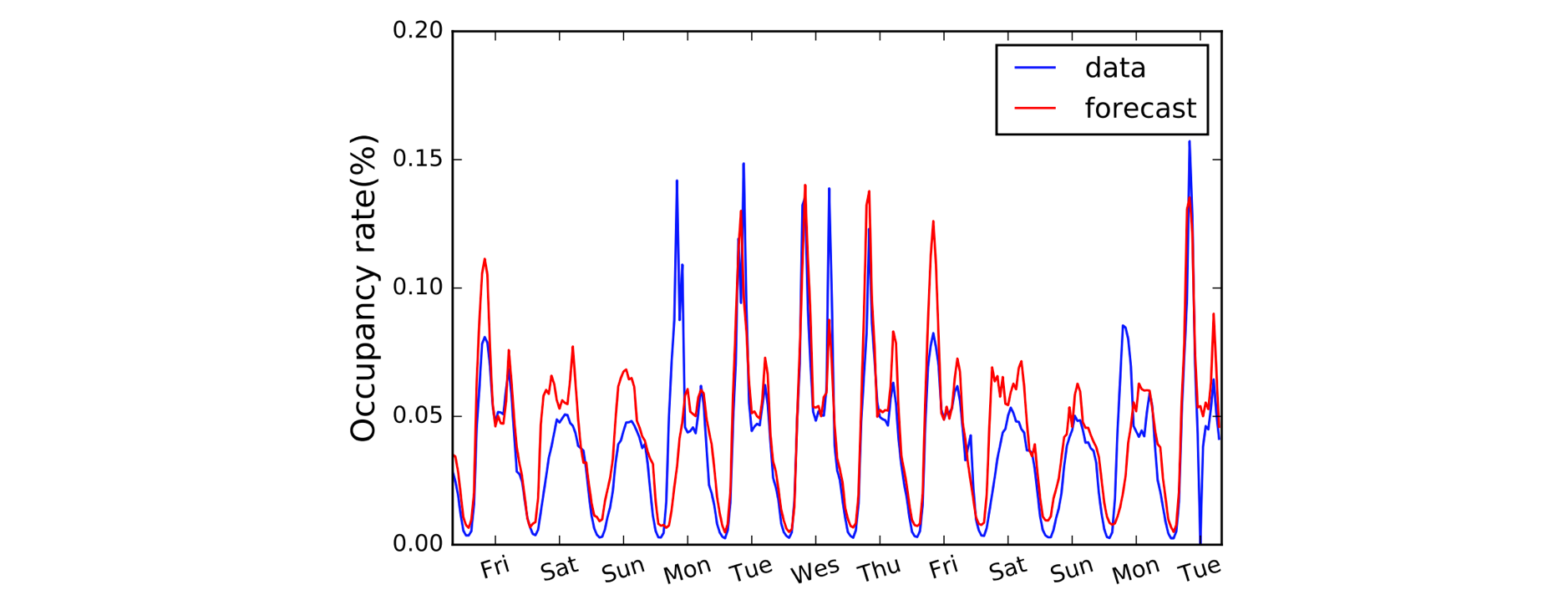
En annan domän som drar nytta av 1D Convolutions är tidsseriemodellering. Liksom tidigare har vi en enda rumslig dimension på våra indata (dvs. tid), och vi vill plocka upp mönster över tidsperioder. Vi kallar ofta denna typ av data för ”sekventiell” eftersom den kan ses som en sekvens av värden. Och den rumsliga dimensionen kallar vi ofta för den ”temporala” dimensionen. Det är också ganska vanligt att använda 1D-konvolutioner före RNN: LSTNet-modellen är ett exempel på detta och dess förutsägelser för trafikprognoser visas nedan.
A, B, C. Det är enkelt som (1,3,3) punkt (2,0,1) = 5.
Med namnkonventioner klargjorda, låt oss nu ta en närmare titt på aritmetiken. Vi har tur eftersom 1D-konvolutioner faktiskt bara är en förenklad version av 2D-konvolutionen!

Vid beräkning av ett enda utdatavärde kan vi tillämpa vår kärna av storlek 3 på det motsvarande stora området på vänster sida av vår inmatningsmatris. Vi beräknar ”punktprodukten” av inmatningsregionen och kärnan, som för att sammanfatta är bara den elementvisa produkten (dvs. multiplicera färgparen) följt av en global summa för att få ett enda värde. Så i det här fallet:
(1*2) + (3*0) + (3*1) = 5
Vi tillämpar samma operation (med samma kärna) på de andra regionerna i inmatningsmatrisen för att få fram den kompletta utmatningsmatrisen på (5,6,7,2); dvs. vi förflyttar kärnan över hela inmatningsmatrisen. Till skillnad från 2D-konvolutioner, där vi förflyttar kärnan i två riktningar, för 1D-konvolutioner förflyttar vi bara kärnan i en enda riktning; vänster/höger i det här diagrammet.
Fördjupning: en 1D-konvolution är inte samma sak som en 1×1 2D-konvolution.
Kodning av saker och ting
Oförvånansvärt nog kommer vi att behöva ett Conv1D Block i Gluon för vår 1D-konvolution. Vi definierar kärnformen som 3, och eftersom vi bara arbetar med en enda kärna i det här exemplet anger vi channels=1.
import mxnet as mxconv = mx.gluon.nn.Conv1D(channels=1,
kernel_size=3)
Vi kan nu skicka vår indata till conv-blocket med hjälp av en fördefinierad kärna.
input_data = mx.nd.array((1,3,3,0,1,2))
kernel = mx.nd.array((2,0,1))# see appendix for definition of `apply_conv`
output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x4 @cpu(0)>
Vad förändras med padding, stride och dilatation?
Vi såg effekten av padding, stride och dilatation i det senaste inlägget om 2D-konvolutioner, och det är mycket liknande för 1D-konvolutioner. Med utfyllnad fyller vi bara ut längs en enda dimension (den temporala dimensionen) den här gången. Vårt diagram representerar tid över den horisontella axeln, så vi fyller på till vänster och höger om indata (och inte över och under som i 2D-konvolutionsexemplet). Vi tillämpar även stegning och utvidgning endast längs den temporala dimensionen. Så ett exempel med padding och stride skulle se ut på följande sätt:

Vi lägger till två ytterligare argument i koden: padding=1 och strides=2.
conv = mx.gluon.nn.Conv1D(channels=1, kernel_size=3,
padding=1, strides=2)output_data = apply_conv(input_data, kernel, conv)
print(output_data)# ]]
# <NDArray 1x1x3 @cpu(0)>
Avancerat: dimensionerna på indata måste överensstämma med en särskild ordning som kallas layout. Som standard förväntar sig 1D-faltningen att tillämpas på indata i formatet ”NCW”, dvs. satsstorlek (N) * kanaler (C) * bredd/tid (W). Och för 2D-konvolutioner är standardvärdet NCHW, dvs. satsstorlek (N) * kanaler (C) * höjd (H) * bredd (W). Kolla in
layout-argumentet iConv1DochConv2D.
.