3D-rekonstruktion

roslaunch ./launch/3d_reconstruction_ros.launch

Därefter måste du exekvera den akademiska applikationen, som kommer att innehålla din kod:

python2 ./3d_reconstruction.py 3d_reconstruction_conf.yml

Hur utför man övningen?

För att utföra övningen måste du redigera filen MyAlgorithm.py och infoga din kod i den, som rekonstruerar 3d-punkter från de två stereovyerna.

Var ska koden infogas?

I filen MyAlgorithm.py,

def algorithm(self):#GETTING THE IMAGES# imageR = self.getImage('right')# imageL = self.getImage('left')#EXAMPLE OF HOW TO PLOT A RED COLORED POINT# position = X, Y, Z# color = R, G, B# self.point.plotPoint(position, color) 

Användningsgränssnitt

• self.getImage('left') – för att få fram den vänstra bilden
• self.getImage('right') – för att få fram den högra bilden
• self.point.PlotPoint(position, color) – för att rita upp punkten i 3d-verktyget

Navigering av gränssnittet för grafiska gränssnittet

Musbaserad: Håll och dra för att flytta runt i miljön. Rulla för att zooma in eller ut

Tangentbordsbaserat: Piltangenter för att flytta runt i miljön. W- och S-tangenterna för att zooma in eller ut

Teori

Inom datorseende och datorgrafik är 3D-rekonstruktion processen att bestämma ett objekts 3D-profil, samt att känna till 3D-koordinaten för varje punkt på profilen. Rekonstruktion kan åstadkommas på följande sätt:

• Hårdvarubaserad: Hårdvarubaserad metod: Hårdvarubaserad metod kräver att vi använder hårdvara som är specifik för rekonstruktionsuppgiften. Användning av strukturerat ljus, laseravståndsmätare, djupmätare och radiometriska metoder är några exempel.

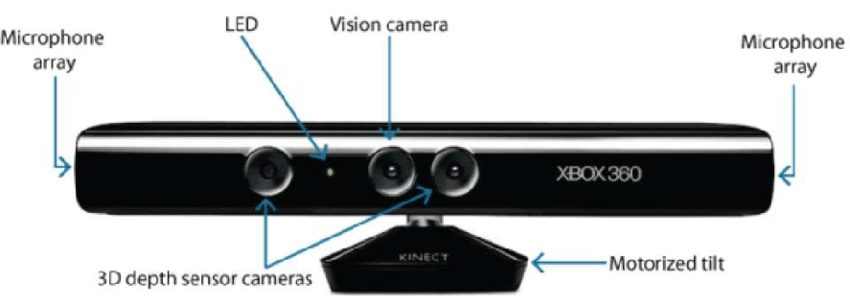
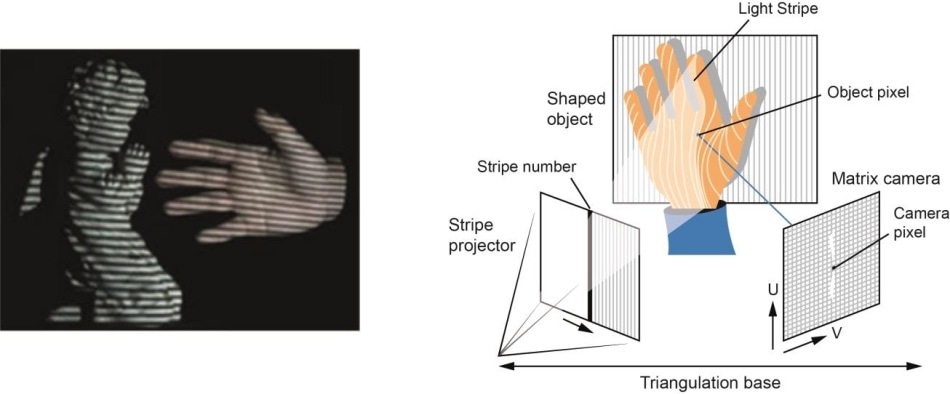
• Programvarubaserad: Programvarubaserad metod: Den programvarubaserade metoden förlitar sig på datorns beräkningskapacitet för att bestämma objektets 3D-egenskaper. Form från skuggning, textur, stereosyn och homografi är några bra metoder.

I den här övningen är vårt huvudsyfte att utföra 3d-rekonstruktion med hjälp av programvarubaserad metod, särskilt stereosyn 3d-rekonstruktion.

Epipolär geometri

När två kameror betraktar en 3D-scen från två olika positioner finns det ett antal geometriska relationer mellan 3D-punkterna och deras projektioner på 2D-bilderna som leder till begränsningar mellan bildpunkterna. Studiet av dessa egenskaper och begränsningar kallas epipolär geometri. Bilden och förklaringen nedan kan generalisera idén:

Antag att en punkt X i 3d-rymden avbildas i två vyer, vid x i den första och x' i den andra. Genom att bakåtprojicera strålarna till sina kameracenter genom bildplanet får vi en plan yta, betecknad med π.

Som vi nu antar att vi bara känner till x kan vi fråga oss hur motsvarande punkt x' är begränsad. Planet π bestäms av baslinjen(linje som förbinder kamerans centrum) och den stråle som definieras av x. Från ovan vet vi att strålen som motsvarar den okända punkten x' ligger i π, och därför ligger punkten x' på skärningslinjen l' mellan π och det andra bildplanet. Denna linje kallas den epipolära linjen som motsvarar x. Detta förhållande hjälper oss att minska sökutrymmet för punkten i den högra bilden från ett plan till en linje. Några viktiga definitioner att notera är:

• Epipolen är skärningspunkten för den linje som förbinder kamerans centrum (baslinjen) med bildplanet.

• Ett epipolärt plan är ett plan som innehåller baslinjen.

• En epipolär linje är skärningspunkten mellan det epipolära planet och bildplanet.

Stereorekonstruktion

Stereorekonstruktion är ett specialfall av ovanstående 3d-rekonstruktion där de två bildplanerna är parallella med varandra och lika avlägsna från den 3d-punkt vi vill plotta.

I det här fallet är den epipolära linjen för båda bildplanen densamma och är parallell med planens bredd, vilket förenklar vår begränsning bättre.

3D-rekonstruktionsalgoritm

Rekonstruktionsalgoritmen består av tre steg:

1. Detektera funktionspunkterna i ett bildplan
2. Detektera funktionspunkten som motsvarar den som hittats ovan
3. Triangulera punkten i 3d-rymden

Låt oss titta på dem en och en

Detektering av funktionspunkter

Detektering av funktionspunkter är ett stort område där flera algoritmer redan är studerade. Algoritmerna Harris Corner Detection och Shi-Tomasi använder egenvärden för att få fram en bra funktionspunkt. Men problemet är att vi behöver många punkter för 3D-rekonstruktion, och dessa algoritmer kommer inte att kunna ge oss ett så stort antal funktionspunkter.

Därför använder vi kantpunkter som våra funktionspunkter. Det kan finnas tvetydigheter i deras upptäckt i nästa steg av algoritmen. Men vårt problem är löst genom att använda kanter som funktionspunkter. En riktigt bra kantdetektor är Canny Edge Detection Algorithm. Algoritmen är ganska enkel och tillförlitlig när det gäller att generera kanter.

Feature Point Extraction

Användningen av den epipolära begränsningen förenklar verkligen tidskomplexiteten för vår algoritm. För allmänna 3d-rekonstruktionsproblem måste vi generera en epipolär linje för varje punkt i en bildruta och sedan söka i det provutrymmet efter motsvarande punkt i den andra bildrutan. Genereringen av den epipolära linjen är också mycket enkel i vårt fall, det är bara den parallella linjens iterpolering från vänster bild till höger bildplan.

Kontrollen av korrespondensen mellan bilderna inbegriper många algoritmer, som summan av kvadrerade skillnader eller energiminimering. Utan att gå särskilt djupt, räcker det också med att använda ett enkelt korrelationsfilter för vårt användningsfall.

Triangulering

Triangulering är i enkla termer bara att beräkna var 3d-punkten kommer att ligga med hjälp av de två bestämda punkterna i bildplanet.

I verkligheten kan bildpunkternas position inte mätas exakt. För allmänna kameror kan det finnas geometriska eller fysiska förvrängningar. Därför ligger mycket matematik bakom att minimera detta fel och beräkna den mest exakta 3d-punktsprojektionen. Se den här länken för en enkel modell.

Hänvisningar

Enkla anvisningar tillhandahålls för att hjälpa dig att lösa övningen 3d_reconstruction. OpenCV-biblioteket används flitigt för den här övningen.

Setup

Med hjälp av övningens API kan vi enkelt hämta bilderna. Efter att ha hämtat bilderna är det också en bra idé att utföra bilateral filtrering av bilderna, eftersom det finns vissa extra detaljer som inte behöver tas med under 3d-rekonstruktionen. Titta på illustrationerna för att se effekterna av att utföra den bilaterala filtreringen.

Beräkning av korrespondenser

OpenCV har redan inbyggda korrelationsfilter som kan anropas via matchTemplate(). Ta hand om extrema fall som kanter och hörn.

En bra observation är att punkterna till vänster kommer att ha korrespondens i den vänstra delen och punkterna till höger kommer att ha korrespondens i den högra delen. Med hjälp av denna observation kan vi enkelt påskynda beräkningen av korrespondensen.

Plottning av punkterna

Endera manuell eller OpenCV-baserad funktion triangulatePoints fungerar bra för triangulering. Se bara till alla matrisformer och matrisstorlekar när du utför de algebraiska implementeringarna.

Håller i minnet skillnaden mellan enkla 3D-koordinater och homogena 4D-koordinater. Kolla in den här videon för mer information. Genom att helt enkelt dividera den kompletta 4d-vektorn med dess fjärde koordinat får vi 3d-koordinaterna.

På grund av användarnas varierande implementeringar kan användaren behöva justera skalan och förskjutningen av de triangulerade punkterna för att göra dem synliga och representerbara i GUI-gränssnittet. Nedskalning av 3D-koordinatvektorn med ett värde mellan 500 och 1000 fungerar bra. Även en förskjutning på 0 till 8 fungerar bra.

Avbildningar