Abelisk grupp | CDhistory

En abelisk grupp är en grupp där elementen växlar (dvs. för alla element och ). Abeliska grupper motsvarar därför grupper med symmetriska multiplikationstabeller.

Alla cykliska grupper är abeliska, men en abelisk grupp är inte nödvändigtvis cyklisk. Alla undergrupper till en abelisk grupp är normala. I en abelisk grupp är varje element i en konjugationsklass för sig självt, och teckentabellen innefattar potenser av ett enda element som är känt som en gruppgenerator.

I Wolfram Language representerar funktionen AbelianGroup den direkta produkten av de cykliska grupperna av graderna , , ….

Ingen generell formel är känd för att ge antalet icke isomorfiska finita grupper av en given gruppordning. Antalet icke isomorfa abeliska finita grupper av en given gruppordning ges dock genom att skriva som

(1)

där är distinkta primfaktorer, då

(2)

där är partitionsfunktionen, som implementeras i Wolframspråket som FiniteAbelianGroupCount. Värdena för för , 2, … är 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, … (OEIS A000688).

De minsta ordningarna för vilka , 2, 3, … icke isomorfiska abelska grupper existerar är 1, 4, 8, 36, 16, 72, 32, 32, 900, 216, 216, 144, 64, 1800, 0, 288, 128, … (OEIS A046056), där 0 betecknar ett omöjligt antal (dvs. inte en produkt av partitionstal) av icke isomorfa abelska grupper. De ”saknade” värdena är 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41, 43, 46, … (OEIS A046064). Det successivt största antalet abelska grupper som en funktion av ordningen är 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, … (OEIS A046054), som förekommer för ordningarna 1, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, … (OEIS A046055).

Kronecker-dekompositionssatsen säger att varje ändlig abelsk grupp kan skrivas som en gruppdirektprodukt av cykliska grupper med primordial potensgruppsordning. Om gruppordningen för en ändlig grupp är ett primtal finns det en enda abelisk grupp med ordningen (betecknad ) och inga icke-abeliska grupper. Om gruppens ordning är ett primtal i kvadrat finns det två abeliska grupper (betecknade och . Om gruppordningen är ett primtal i kubik finns det tre abeliska grupper (betecknade , och ), och totalt fem grupper. Om ordningen är en produkt av de två primtalen och finns det exakt en abelsk grupp med gruppordningen (betecknad ).

Ett annat intressant resultat är att om betecknar antalet icke isomorfa abelska grupper av gruppordning , så

(3)

där är Riemanns zeta-funktion.

Antalen av abelska grupper av ordningen ges av 1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15, 17, 18, 19, 20, 25, … (OEIS A063966) för , 2, …. Srinivasan (1973) har också visat att

(4)

där

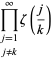			(5)
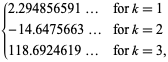			(6)

(OEIS A021002, A084892 och A084893) och är återigen Riemanns zetafunktion. Observera att Richert (1952) felaktigt gav . Summorna kan också skrivas i de explicita formerna