Ta en titt på de senaste artiklarna

Abstract

Ljuset färdas genom ett vakuum med hastigheten c oberoende av ljuskällans rörelse eller observatörens referensram. Följaktligen krävs det en viss tid för att ljuset ska färdas från en ljuskälla till en observatör i rymden, så att ljusets utsändning och observationen av det utsända ljuset inte är samtidiga. På grundval av dessa överväganden föreslås en metod för att mäta en observatörs absoluta hastighet, som skulle kunna användas för att bestämma en rymdfarkosts rörelsetillstånd inifrån en sluten kabin. I denna studie introduceras också en ny förklaring av Lorentztransformationen.

Nyckelord

koordinatsystem, referenssystem, rörelse, absolut hastighet, relativitetsteori, Lorentztransformation, tid, rum, observatör, ljuskälla
I följande analys presenteras ett praktiskt tillvägagångssätt för att mäta en observatörs absoluta hastighet, som skulle kunna användas för att bestämma en rymdfarkosts rörelsestatus inifrån en stängd kabin. Begreppet absolut hastighet avser i allmänhet en enhetlig standardhastighet för de olika objekten i ett fysiskt system i förhållande till ett postulerat orörligt rum som existerar oberoende av de fysiska objekt som ingår i det (dvs. ett absolut rum). Här presenterar vi ett tillvägagångssätt som bygger på stel kinematik för att visa att en observatörs absoluta hastighet kan bestämmas utifrån det faktum att ljuset färdas genom ett vakuum med hastigheten c oberoende av ljuskällans rörelse eller rörelsen i observatörens referensram. Följaktligen krävs det en viss tid för att ljuset ska färdas från en ljuskälla till en observatör i rymden, så att ljuset som sänds ut och observationen av det utsända ljuset inte är samtidiga.
I den föreslagna analysen tillhandahåller vi först följande konventioner för de aktuella koordinatsystemen. Vi utgår från ett kartesiskt koordinatsystem som består av tre parvis vinkelräta axlar som utgår från punkten (0,0,0), där varje punkt P i rymden kan definieras genom sina koordinater längs x-, y- och z-axlarna, som representeras av ett ordnat par av reella tal (x,y,z). Ett tröghetsreferenssystem S antas representeras av ett rektangulärt rymdkoordinatsystem (x,y,z) vars ursprung är O. En serie standardklockor (benämnda S-klockor) är placerade på stationära punkter i S. S-klockorna är ömsesidigt kalibrerade (dvs. de ger likvärdiga avläsningar vid samma tidpunkt) på grundval av sändning och mottagning av en ljussignal. Närmare bestämt projiceras vid tiden tA en ljusstråle från klocka A till klocka B, som sedan vid tiden tB reflekteras av klocka B tillbaka mot klocka A och anländer till klocka A vid tiden tA’. Om är de två klockorna kalibrerade. För varje händelse som befinner sig vid koordinaterna x,y,z ges dess tidskoordinat t av avläsningen av den händelserelaterade S-klockan. På samma sätt upprättas ett annat tröghetsreferenssystem S’ baserat på ett andra rektangulärt rymdkoordinatsystem (x’,y’,z’) vars ursprung är O’, och en annan serie ömsesidigt kalibrerade standardklockor (S’-klockor) är placerade i stationära punkter i referenssystemet S’. För varje händelse som befinner sig vid koordinaterna x’,y’,z’ ges dess tidskoordinat t’ av avläsningen av den händelserelaterade S’-klockan.
Eftersom de rumsliga och tidsmässiga koordinaternas respektive ursprung, liksom koordinataxlarnas riktningar, i stor utsträckning kan väljas godtyckligt, baseras de relationer mellan S och S’ som används här på följande konventioner, som har tillämpats för enkelhetens skull.
(1) Vid en viss tidpunkt är de två systemens ursprung och koordinataxlar överlagrade, och klockorna vid O respektive O’ är inställda på noll, dvs, .
(2) Axlarna x och x’ sammanfaller i riktningen för den relativa rörelsen av S och S’; således är x och x’ alltid sammanfallande, medan y och y’ samt z och z’ är parallella.
(3) S’ rör sig i S’:s +x-riktning.
Den föreslagna analysen bygger på den grundläggande principen att ljuset i ett vakuum rör sig med konstant hastighet c, oavsett om observatören eller ljuskällan är rörliga eller inte. Således definierar vi härmed observatörens absoluta hastighet U, som antas vara linjär och enhetlig, som , där f(φ) representerar en funktion av det geometriska förhållandet mellan riktningen för en ljussignal och riktningen för U, som här benämns φ.
I den föreslagna analysen ges två nya förklaringar till tidens och längdens relativitet, som skiljer sig från Einsteins förklaringar (se ”Om rörliga kroppars elektrodynamik”). Dessa förklaringar presenteras i följande avsnitt.

Tidens relativitet

Enligt ljusets ändliga hastighet krävs det en viss tid för ljuset att färdas från en ljuskälla till en observatör i rymden. Man kan därför dra slutsatsen att ljusemission och ljusobservation inte kan vara samtidiga. Med utgångspunkt i ljusets konstanta hastighet och de förhållanden som illustreras i figur 1 definierar vi följande faktorer. Positionerna för en ljuskälla och en observatör vid , då ljuskällan avger ljus (betecknad som händelse R), ges som A respektive H0. Under ljusets utbredningsperiod från till färdas observatören en sträcka U∙T från position H0 till H, varpå observatören tar emot det utsända ljuset. Följaktligen definierar vi som avståndet l mellan observatörens position vid mottagandet av ljussignalen vid och ljuskällans position när ljuset sänds ut vid . På grund av ljusets konstanta hastighet är . Avståndet motsvarar U∙T. Slutligen definierar vi som avståndet l0 mellan observatörens position vid och ljuskällans position vid . Här introducerar vi en betraktelse av observatörens position vid , som tidigare inte ansågs ha någon fysisk betydelse. Om observatörens och ljuskällans rörelsetillstånd är likvärdiga är l0 givet, så att U kan beräknas via de triangulära relationer som illustreras i ,Figur 1.
I detta arbete mäts tiden för en händelse med hjälp av följande metod. Både observatören och en klocka placeras vid ursprunget. När den ljussignal som representerar en händelse når observatören kommer ljusets ankomsttid att motsvara den tid som klockan anger. Fördelen med korrespondensen är att den alltid är relaterad till positionen för den observatör som använder klockan. Som framgår av figur 1 kan den rumsliga punkten O3 definieras utifrån ljuskällans position när ljuset sänds ut vid , och den rumsliga punkten O2 kan definieras utifrån observatörens position när ljuset tas emot vid . Det är dock inte uppenbart hur man definierar den rumsliga punkten O1 där observatören befinner sig när ljuskällan sänder ut ljus vid . För att lösa detta problem införs begreppen absolut vila (dvs. ) och absolut rörelse (dvs. ). Vi ersätter den enda rörliga observatören vid H0 och H med två observatörer H1 och H2 i vila vid rumspunkterna O1 respektive O2, medan ljuskällan A är i vila vid rumspunkten O3. Var och en av observatörerna och ljuskällan använder kalibrerade standardklockor, och A sänder ut en ljussignal vid , som betecknas som händelse R0. När observatör H1 tar emot ljussignalen som färdas med c är klockans avläsning T0, och när H2 tar emot den är avläsningen T. Avstånden och kan således definieras på grundval av ljussignalens respektive färdtider enligt följande:
, (1)
och
. (2)
Enligt de triangulära relationerna som visas i figur 1 ges transformationen av händelsen R0 mellan observatörerna H1 och H2 enligt följande:
(3)
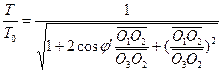(4)
Här är vinkeln mellan linjen O3O1 och x-axeln, och är vinkeln mellan linjen O3O2 och x-axeln.
Vid återgång till förhållandet med en enda rörlig observatör antar vi att i system S använder både observatör H och ljuskälla A en kalibrerad standardklocka. Vid tidpunkten för händelsen R befinner sig ljuskälla A i den rumsliga punkten O3 och observatör H befinner sig i O1. Det ögonblick då ljussignalen når den rumsliga punkten O1 motsvarar en klockavläsning i S på T0. När observatör H tar emot ljussignalen är avläsningen T, och H befinner sig vid O2.
H kan naturligtvis inte observera händelsen R i punkt O1. För att lösa detta problem placeras en annan observatör H- i system S vid punkt O1 som motsvarar , där H-:s position används för att definiera den rumsliga punkten O1. Därefter kan transformationen av händelsen R mellan observatörerna H- och H erhållas genom ekvation (3) enligt följande.
(5)
Därmed kan ekvationerna (3) och (4) skrivas om på följande sätt:
(6)
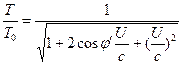(7)
e observerar också att för förenklas ekvationerna (6) och (7) till följande.
(8)
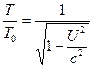(9)
Med utgångspunkt i ovanstående analys kan därför en enkel metod för att bestämma U erhållas från ekvation (6), givet att (φ) är känd.
För enkelhetens skull väljs en ljuskälla med ett likvärdigt rörelsetillstånd som observatörernas som referensram. En observatör är placerad i mitten av en rak styv stång i enhetlig linjär rörelse, och ljussignaler från olika positioner på stången anländer till observatören vid olika tidpunkter. Observatören upptäcker stavens avböjning vid observatörens position med en avböjningsvinkel som kan erhållas från ekvation (8).
Genom denna metod kan rörelsetillståndet för en rymdfarkost bestämmas från en stängd kabin.

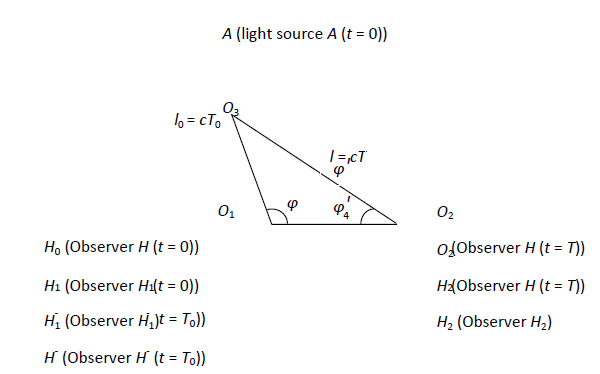
Figur 1: rörelsetillstånd för observatören och ljuskällan

Längderelativiteten

I analysen ovan har två längder införts, dvs. och . I detta fall betraktar vi längden på en stång som antas vara en stationär styv stång med längden L inom sitt koordinatsystem, för vilken L mäts med en stationär stavmätare, och där stångens axel sammanfaller med x-axeln i ett koordinatsystem som rör sig med en enhetlig linjär rörelse längs +x-riktningen med en absolut hastighet U. Det antas att L bestäms genom de två operationer som definieras nedan.
(a) Observatören befinner sig i samma rörliga koordinatsystem som staven och stavmätaren, och L mäts genom att staven och stavmätaren överlagras.
(b) Med hjälp av flera klockor som är placerade i stationära koordinater och som rör sig synkroniserat mäter observatören positionerna för stavens två ändar i stationära koordinater vid ett visst ögonblick t, och avståndet mellan de två positionerna mäts med den stationära stavmätaren. är den längd som beräknats från operation (a) och som här betecknas som stångens längd i den rörliga koordinaten. är den längd som beräknats från operation (b) och som här betecknas som längden på en rörlig stav i den stationära koordinaten. Det är uppenbart att och är olika.
Vi antar att observatör H- i system S befinner sig i samma rörelsetillstånd som H. Då, som visas i figur 1, befinner sig H- i punkt O1 när han tar emot ljussignalen vid , och samtidigt befinner sig observatör H i punkt O4. Därför är t=0,04
avståndet mellan H- och H vid , och
. (10)
är den sträcka som observatör H tillryggalägger under intervallet från T0 till T, så att
. (11)
är avståndet mellan H- vid och H vid , så att
. (12)
Så kan följande uttryck härledas:
(13)
Nästan ska vi betrakta koordinat- och tidstransformationerna mellan två rörliga koordinatsystem, som båda rör sig med en enhetlig linjär hastighet, vilket representerar en ny förklaring av Lorentztransformationen.
Antag att observatör H (i system S), observatör H’ (i system S’) och ljuskälla A” (i system S”) alla använder kalibrerade standardklockor individuellt, och att ljuskälla A” vid avger en ljussignal, betecknad som händelse R”. Vid tidpunkten för händelsen R”’ befinner sig A” i punkt O3, och observatörerna H och H’ sammanfaller. När observatör H tar emot ljussignalen är S-klockans avläsning T, och H befinner sig i punkt O1. När observatör H’ tar emot ljussignalen är avläsningen av klockan S’ T’, och H’ befinner sig i punkt O2. Då kan transformationen av händelsen R”’ mellan observatörerna H’ och H beräknas från ekvation (3), där
. (14)
Här är u den relativa hastigheten mellan observatörerna H’ och H, vilket ger följande transformationer.
(15)
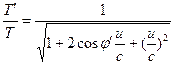(16)
Från kan följande relationer härledas:
. (17)
När och förenklas ekvation (16) till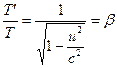
. (18)
Därmed kan följande transformationsrelationer härledas:
, (19)
, (20)
, (21)
. (22)
För övrigt, när ,
, (23)
och
, (24)
, (25)
, (26)
. (27)