Toleransintervall
Detta avsnitt innehåller statistiska uppgifter för ensidiga och dubbelsidiga toleransintervall.
Normalfördelningsbaserade intervall
Ensidigt intervall
Det ensidiga intervallet beräknas på följande sätt:
Understa gränsen = 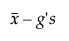
Övre gränsen = 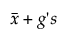
där
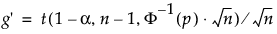
s är standardavvikelsen
t är kvantilen från det icke-central t-fördelning
Φ-1 är standardnormalkvantilen
Tvåsidigt intervall
Det tvåsidiga intervallet beräknas på följande sätt:
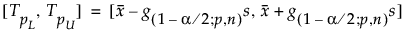
där s är standardavvikelsen och g(1-α/2; p,n) är en konstant.
För att bestämma g, betrakta den del av populationen som omfattas av toleransintervallet. Tamhane och Dunlop (2000) anger denna fraktion på följande sätt:
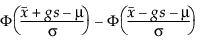
där Φ betecknar standardnormal cdf (kumulativ fördelningsfunktion).
Därmed löser g följande ekvation:
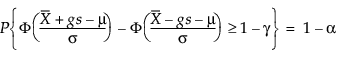
där 1 – γ är andelen av alla framtida observationer som ingår i toleransintervallet.
För mer information om toleransintervall baserade på normalfördelning, se tabell J.1.a, J.1b, J.6a och J.6b i Meeker et al. (2017).
Nonparametriska intervall
En ensidig nedre gräns
Den nedre 100(1 – α)% ensidiga toleransgränsen för att innehålla minst en andel β av den samplade fördelningen från ett stickprov av storlek n är orderstatistiken x(l). Indexet l beräknas på följande sätt:
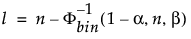
där Φ-1bin(1-α, n, β) är den (1 – α)-te kvantilen av binomialfördelningen med n försök och sannolikheten för framgång β.
Den faktiska konfidensnivån beräknas som Φbin(n-l, n, β), där Φbin(x, n, β) är sannolikheten för att en binomialfördelad slumpvariabel med n försök och sannolikhet för framgång β är mindre än eller lika med x.
Bemärk att för att beräkna ett nedre ensidigt toleransintervall utan fördelning måste provstorleken n vara minst lika stor som 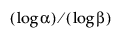 .
.
En ensidig övre gräns
Den övre 100(1 – α)% ensidiga toleransgränsen för att innehålla minst en andel β av den samplade fördelningen från ett prov av storlek n är orderstatistiken x(u). Indexet u beräknas på följande sätt:
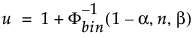
där Φ-1bin(1-α, n, β) är den (1 – α)-te kvantilen av binomialfördelningen med n försök och sannolikhet för framgång β.
Den faktiska konfidensnivån beräknas som Φbin(u-1, n, β), där Φbin(x, n, β) är sannolikheten för att en binomialfördelad slumpvariabel med n försök och sannolikhet för framgång β är mindre än eller lika med x.
Observera att för att kunna beräkna ett övre ensidigt toleransintervall fritt från fördelning måste urvalsstorleken n vara minst lika stor som 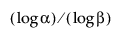 .
.
Tvåsidigt intervall
Det 100(1 – α)% tvåsidiga toleransintervallet för att innehålla minst en andel β av den provtagna fördelningen från ett urval av storlek n beräknas på följande sätt:
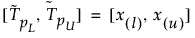
där x(i) är den i:e statistiken och l och u beräknas på följande sätt:
Let ν = n – Φ-1bin(1-α, n, β), där Φ-1bin(1-α, n, β) är den (1 – α)-te kvantilen för binomialfördelningen med n försök och framgångssannolikhet β. Om ν är mindre än 2 kan ett tvåsidigt fördelningsfritt toleransintervall inte beräknas. Om ν är större än eller lika med 2 är l = floor(ν/2) och u = floor(n + 1 – ν/2).
Den faktiska konfidensnivån beräknas som Φbin(u-l-1, n, β), där Φbin(x, n, β) är sannolikheten för att en binomialfördelad slumpmässig variabel med n försök och sannolikhet för framgång β är mindre än eller lika med x.
Observera att för att beräkna ett tvåsidigt fördelningsfritt toleransintervall måste provstorleken n vara minst lika stor som n i följande ekvation:

För mer information om fördelningsfria toleransintervall, se Meeker m.fl. (2017, sek. 5.3).