Toleranssivälit
Tämä osio sisältää tilastollisia yksityiskohtia yksipuolisia ja kaksipuolisia toleranssivälejä varten.
Normaalijakaumaan perustuvat toleranssivälit
Yksipuolinen väli
Yksipuolinen väli lasketaan seuraavasti:
Alaraja = 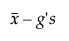
Yläraja = 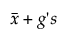
joissa
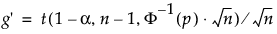
s on keskihajonta
t on kvanttiili ei-ei-ei-ei-ei-ei-ei-ei-ei-ei-ei-ei-ei.keskeisestä t-jakaumasta
Φ-1 on tavallinen normaali kvantiili
Kaksipuolinen väli
Kaksipuolinen väli lasketaan seuraavasti:
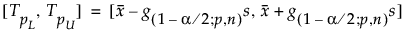
jossa s on keskihajonta ja g(1-α/2; p,n) on vakio.
G:n määrittämiseksi tarkastellaan sitä osuutta populaatiosta, jonka toleranssiväli kattaa. Tamhane ja Dunlop (2000) antavat tämän osuuden seuraavasti:
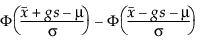
jossa Φ tarkoittaa tavallista normaalia cdf:tä (kumulatiivista jakaumafunktiota).
Siten g ratkaisee seuraavan yhtälön:
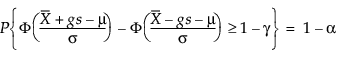
jossa 1 – γ on kaikkien tulevien havaintojen murto-osa, joka sisältyy toleranssiväliin.
Lisätietoa normaalijakaumaan perustuvista toleranssiväleistä löytyy taulukoista J.1.a, J.1b, J.6a ja J.6b julkaisussa Meeker et al. (2017).
Nonparametriset toleranssirajat
Yksisivuinen alaraja
Alempi 100(1 – α)%:n yksisivuinen toleranssiraja, joka pitää sisällään vähintään osuuden β otosjakaumasta koko n:n suuruisesta otoksesta, on järjestystilasto x(l). Indeksi l lasketaan seuraavasti:
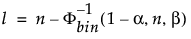
jossa Φ-1bin(1-α, n, β) on binomijakauman (1 – α)kolmas kvanttiili, jossa on n kokeilua ja onnistumisen todennäköisyys β.
Tosiasiallinen luottamustaso lasketaan muodossa Φbin(n-l, n, β), missä Φbin(x, n, β) on todennäköisyys sille, että binomijakautunut satunnaismuuttuja, jossa on n kokeilua ja onnistumisen todennäköisyys β, on pienempi tai yhtä suuri kuin x.
Huomaa, että alemman yksipuolisen jakaumattoman toleranssivälin laskemiseksi otoskoon n on oltava vähintään yhtä suuri kuin 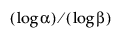 .
.
Yksipuolinen yläraja
Ylimmän 100(1 – α)%:n yksipuolisen toleranssivälin yläraja, jotta se sisältäisi vähintään osuuden β otosjakaumasta, joka on otettu n-kokoisesta näytteestä, on järjestystilasto x(u). Indeksi u lasketaan seuraavasti:
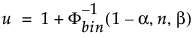
jossa Φ-1bin(1-α, n, β) on binomijakauman (1 – α)kolmas kvanttiili, jossa on n kokeilua ja onnistumisen todennäköisyys β.
Tosiasiallinen luottamustaso lasketaan muodossa Φbin(u-1, n, β), missä Φbin(x, n, β) on todennäköisyys sille, että binomijakautunut satunnaismuuttuja, jossa on n kokeilua ja onnistumistodennäköisyys β, on pienempi tai yhtä suuri kuin x.
Huomaa, että ylemmän yksipuolisen jakaumattoman toleranssivälin laskemiseksi otoskoon n on oltava vähintään yhtä suuri kuin 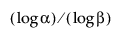 .
.
Kaksipuolinen toleranssiväli
Kaksipuolinen 100(1 – α)%:n toleranssiväli, joka sisältää vähintään osuuden β otosjakaumasta otoskoon n kokoisesta otoksesta, lasketaan seuraavasti:
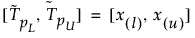
jossa x(i) on i:nnen kertaluvun tilasto ja l ja u lasketaan seuraavasti:
Let ν = n – Φ-1bin(1-α, n, β), missä Φ-1bin(1-α, n, β) on binomijakauman, jossa on n koeajoa ja onnistumistodennäköisyys β, (1 – α)-lk:n kvartiili. Jos ν on pienempi kuin 2, kaksipuolista jakaumavapaata toleranssiväliä ei voida laskea. Jos ν on suurempi tai yhtä suuri kuin 2, l = floor(ν/2) ja u = floor(n + 1 – ν/2).
Tosiasiallinen luottamustaso lasketaan muodossa Φbin(u-l-1, n, β), jossa Φbin(x, n, β) on todennäköisyys sille, että binomijakautuneen satunnaismuuttujan, jossa on n kokeilua ja onnistumistodennäköisyys β, todennäköisyys on pienempi tai yhtä suuri kuin x.
Huomaa, että kaksipuolisen jakaumattoman toleranssivälin laskemiseksi otoskoon n on oltava vähintään yhtä suuri kuin n seuraavassa yhtälössä:

Lisätietoa jakaumattomista toleranssiväleistä löydät Meeker et al. (2017, sek. 5.3).